Pierre Minssen
Des-q: a quantum algorithm to construct and efficiently retrain decision trees for regression and binary classification
Sep 22, 2023Abstract:Decision trees are widely used in machine learning due to their simplicity in construction and interpretability. However, as data sizes grow, traditional methods for constructing and retraining decision trees become increasingly slow, scaling polynomially with the number of training examples. In this work, we introduce a novel quantum algorithm, named Des-q, for constructing and retraining decision trees in regression and binary classification tasks. Assuming the data stream produces small increments of new training examples, we demonstrate that our Des-q algorithm significantly reduces the time required for tree retraining, achieving a poly-logarithmic time complexity in the number of training examples, even accounting for the time needed to load the new examples into quantum-accessible memory. Our approach involves building a decision tree algorithm to perform k-piecewise linear tree splits at each internal node. These splits simultaneously generate multiple hyperplanes, dividing the feature space into k distinct regions. To determine the k suitable anchor points for these splits, we develop an efficient quantum-supervised clustering method, building upon the q-means algorithm of Kerenidis et al. Des-q first efficiently estimates each feature weight using a novel quantum technique to estimate the Pearson correlation. Subsequently, we employ weighted distance estimation to cluster the training examples in k disjoint regions and then proceed to expand the tree using the same procedure. We benchmark the performance of the simulated version of our algorithm against the state-of-the-art classical decision tree for regression and binary classification on multiple data sets with numerical features. Further, we showcase that the proposed algorithm exhibits similar performance to the state-of-the-art decision tree while significantly speeding up the periodic tree retraining.
Quantum Deep Hedging
Mar 29, 2023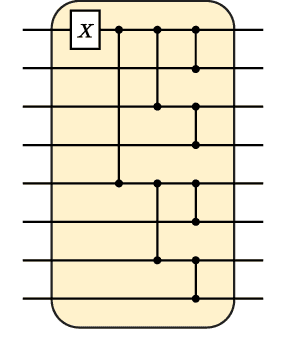
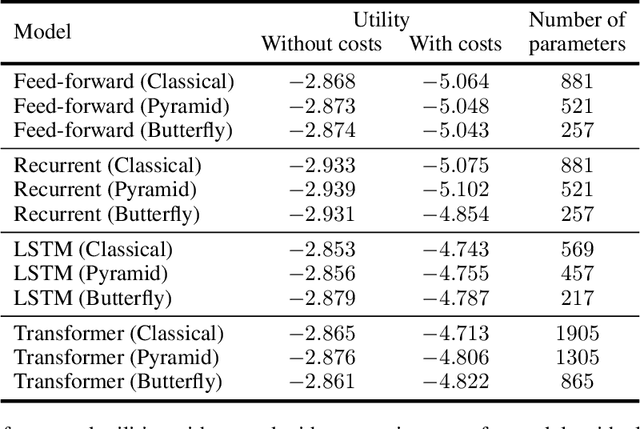
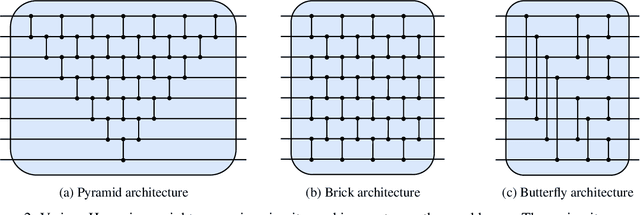
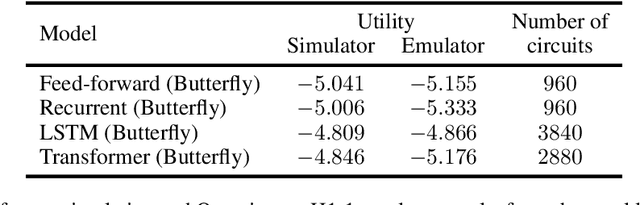
Abstract:Quantum machine learning has the potential for a transformative impact across industry sectors and in particular in finance. In our work we look at the problem of hedging where deep reinforcement learning offers a powerful framework for real markets. We develop quantum reinforcement learning methods based on policy-search and distributional actor-critic algorithms that use quantum neural network architectures with orthogonal and compound layers for the policy and value functions. We prove that the quantum neural networks we use are trainable, and we perform extensive simulations that show that quantum models can reduce the number of trainable parameters while achieving comparable performance and that the distributional approach obtains better performance than other standard approaches, both classical and quantum. We successfully implement the proposed models on a trapped-ion quantum processor, utilizing circuits with up to $16$ qubits, and observe performance that agrees well with noiseless simulation. Our quantum techniques are general and can be applied to other reinforcement learning problems beyond hedging.
Quantum Machine Learning for Finance
Sep 09, 2021Abstract:Quantum computers are expected to surpass the computational capabilities of classical computers during this decade, and achieve disruptive impact on numerous industry sectors, particularly finance. In fact, finance is estimated to be the first industry sector to benefit from Quantum Computing not only in the medium and long terms, but even in the short term. This review paper presents the state of the art of quantum algorithms for financial applications, with particular focus to those use cases that can be solved via Machine Learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge