Imperfect-Recall Games: Equilibrium Concepts and Their Complexity

We investigate optimal decision making under imperfect recall, that is, when an agent forgets information it once held before. An example is the absentminded driver game, as well as team games in which the members have limited communication capabilities. In the framework of extensive-form games with imperfect recall, we analyze the computational complexities of finding equilibria in multiplayer settings across three different solution concepts: Nash, multiselves based on evidential decision theory (EDT), and multiselves based on causal decision theory (CDT). We are interested in both exact and approximate solution computation. As special cases, we consider (1) single-player games, (2) two-player zero-sum games and relationships to maximin values, and (3) games without exogenous stochasticity (chance nodes). We relate these problems to the complexity classes P, PPAD, PLS, $\Sigma_2^P$ , $\exists$R, and $\exists \forall$R.

The Computational Complexity of Single-Player Imperfect-Recall Games

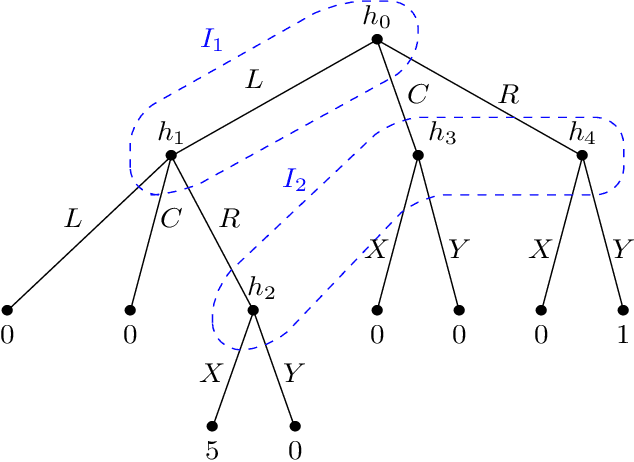
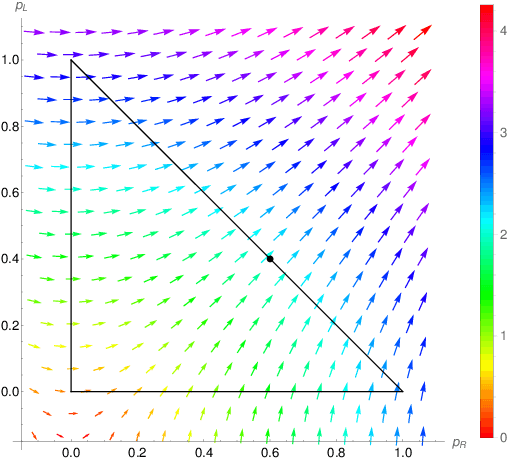
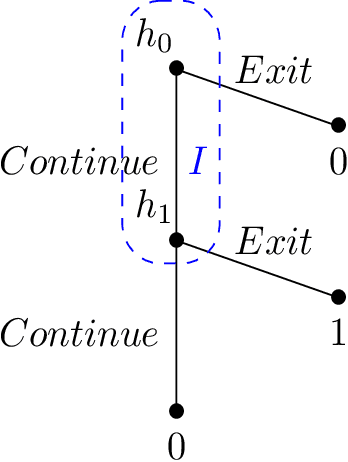
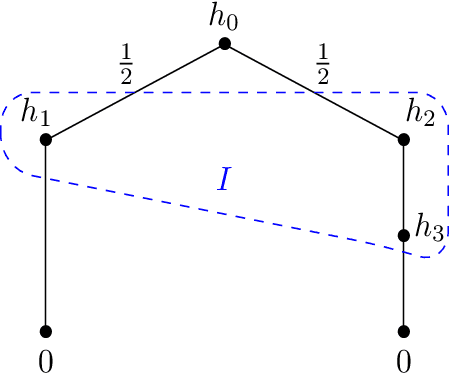
We study single-player extensive-form games with imperfect recall, such as the Sleeping Beauty problem or the Absentminded Driver game. For such games, two natural equilibrium concepts have been proposed as alternative solution concepts to ex-ante optimality. One equilibrium concept uses generalized double halving (GDH) as a belief system and evidential decision theory (EDT), and another one uses generalized thirding (GT) as a belief system and causal decision theory (CDT). Our findings relate those three solution concepts of a game to solution concepts of a polynomial maximization problem: global optima, optimal points with respect to subsets of variables and Karush-Kuhn-Tucker (KKT) points. Based on these correspondences, we are able to settle various complexity-theoretic questions on the computation of such strategies. For ex-ante optimality and (EDT,GDH)-equilibria, we obtain NP-hardness and inapproximability, and for (CDT,GT)-equilibria we obtain CLS-completeness results.

The Complexity of Gradient Descent: CLS = PPAD $\cap$ PLS

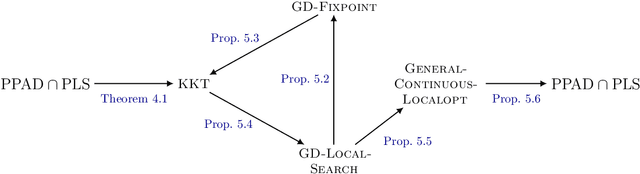
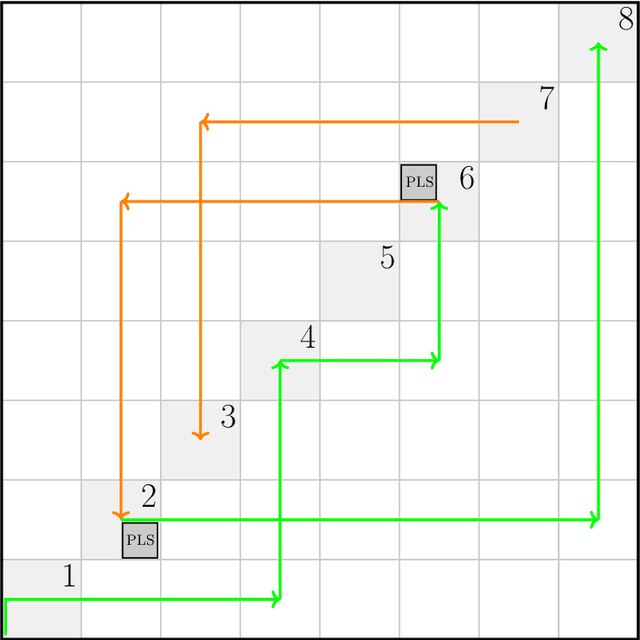
We study search problems that can be solved by performing Gradient Descent on a bounded convex polytopal domain and show that this class is equal to the intersection of two well-known classes: PPAD and PLS. As our main underlying technical contribution, we show that computing a Karush-Kuhn-Tucker (KKT) point of a continuously differentiable function over the domain $[0,1]^2$ is PPAD $\cap$ PLS-complete. This is the first natural problem to be shown complete for this class. Our results also imply that the class CLS (Continuous Local Search) - which was defined by Daskalakis and Papadimitriou as a more "natural" counterpart to PPAD $\cap$ PLS and contains many interesting problems - is itself equal to PPAD $\cap$ PLS.

The Complexity of Splitting Necklaces and Bisecting Ham Sandwiches

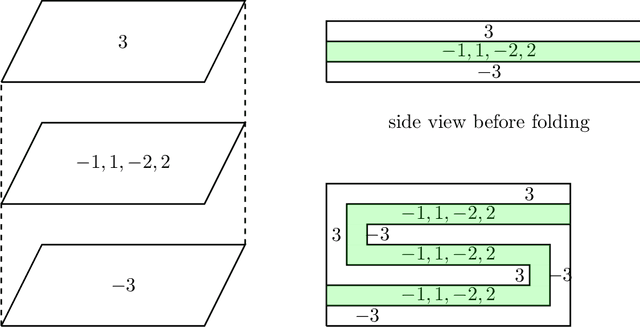
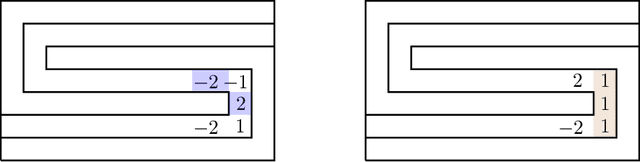
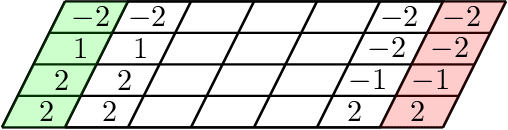
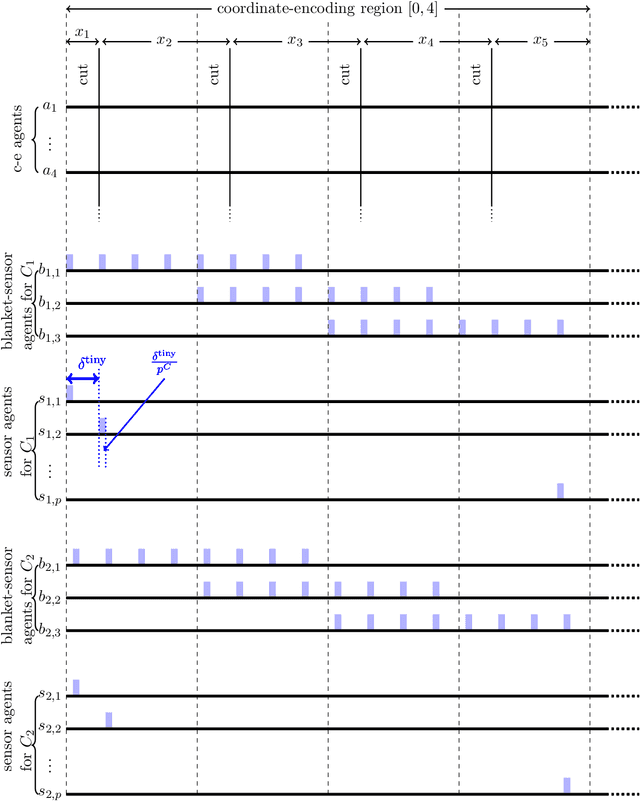
We resolve the computational complexity of two problems known as NECKLACE-SPLITTING and DISCRETE HAM SANDWICH, showing that they are PPA-complete. For NECKLACE SPLITTING, this result is specific to the important special case in which two thieves share the necklace. We do this via a PPA-completeness result for an approximate version of the CONSENSUS-HALVING problem, strengthening our recent result that the problem is PPA-complete for inverse-exponential precision. At the heart of our construction is a smooth embedding of the high-dimensional M\"obius strip in the CONSENSUS-HALVING problem. These results settle the status of PPA as a class that captures the complexity of "natural" problems whose definitions do not incorporate a circuit.

Learning Convex Partitions and Computing Game-theoretic Equilibria from Best Response Queries

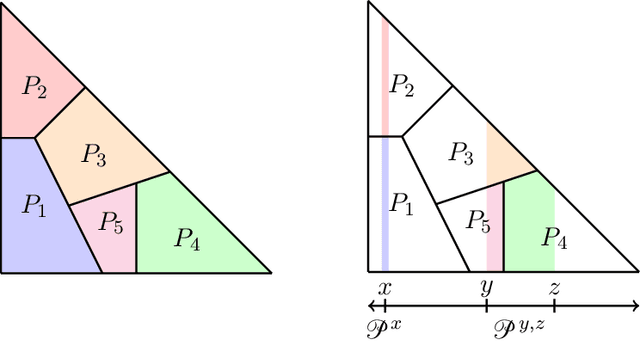
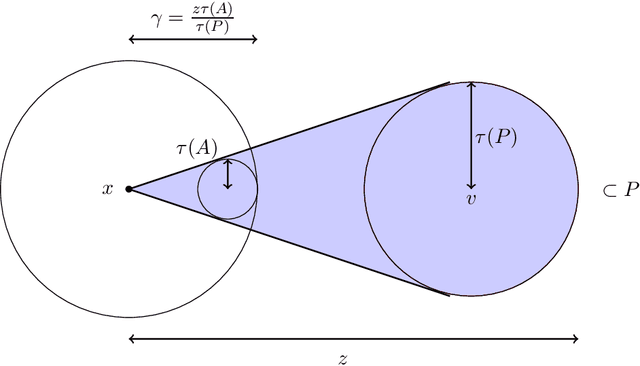
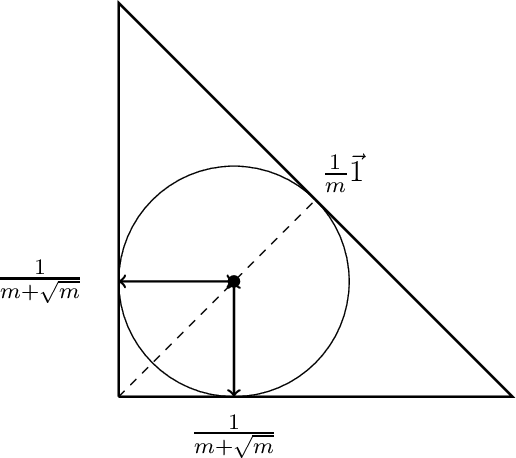
Suppose that an $m$-simplex is partitioned into $n$ convex regions having disjoint interiors and distinct labels, and we may learn the label of any point by querying it. The learning objective is to know, for any point in the simplex, a label that occurs within some distance $\epsilon$ from that point. We present two algorithms for this task: Constant-Dimension Generalised Binary Search (CD-GBS), which for constant $m$ uses $poly(n, \log \left( \frac{1}{\epsilon} \right))$ queries, and Constant-Region Generalised Binary Search (CR-GBS), which uses CD-GBS as a subroutine and for constant $n$ uses $poly(m, \log \left( \frac{1}{\epsilon} \right))$ queries. We show via Kakutani's fixed-point theorem that these algorithms provide bounds on the best-response query complexity of computing approximate well-supported equilibria of bimatrix games in which one of the players has a constant number of pure strategies. We also partially extend our results to games with multiple players, establishing further query complexity bounds for computing approximate well-supported equilibria in this setting.

PAC Classification based on PAC Estimates of Label Class Distributions

A standard approach in pattern classification is to estimate the distributions of the label classes, and then to apply the Bayes classifier to the estimates of the distributions in order to classify unlabeled examples. As one might expect, the better our estimates of the label class distributions, the better the resulting classifier will be. In this paper we make this observation precise by identifying risk bounds of a classifier in terms of the quality of the estimates of the label class distributions. We show how PAC learnability relates to estimates of the distributions that have a PAC guarantee on their $L_1$ distance from the true distribution, and we bound the increase in negative log likelihood risk in terms of PAC bounds on the KL-divergence. We give an inefficient but general-purpose smoothing method for converting an estimated distribution that is good under the $L_1$ metric into a distribution that is good under the KL-divergence.