The Complexity of Gradient Descent: CLS = PPAD $\cap$ PLS

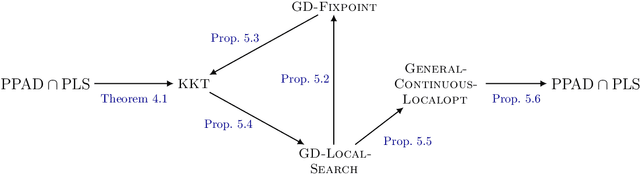
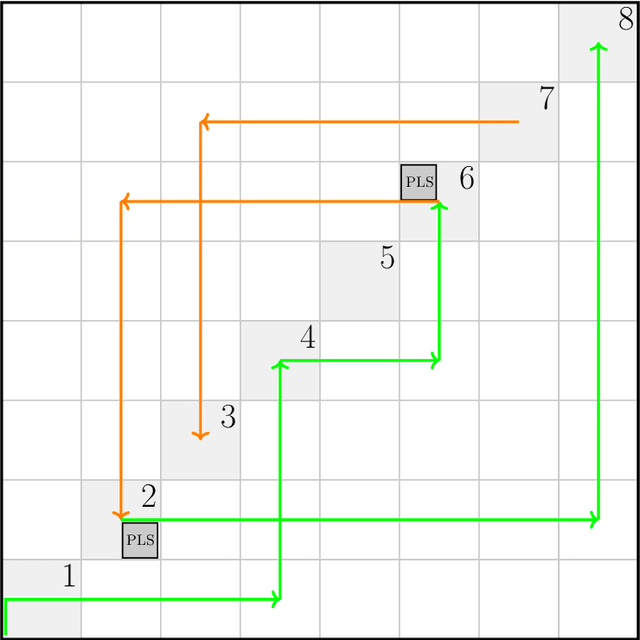
We study search problems that can be solved by performing Gradient Descent on a bounded convex polytopal domain and show that this class is equal to the intersection of two well-known classes: PPAD and PLS. As our main underlying technical contribution, we show that computing a Karush-Kuhn-Tucker (KKT) point of a continuously differentiable function over the domain $[0,1]^2$ is PPAD $\cap$ PLS-complete. This is the first natural problem to be shown complete for this class. Our results also imply that the class CLS (Continuous Local Search) - which was defined by Daskalakis and Papadimitriou as a more "natural" counterpart to PPAD $\cap$ PLS and contains many interesting problems - is itself equal to PPAD $\cap$ PLS.

Market Making via Reinforcement Learning

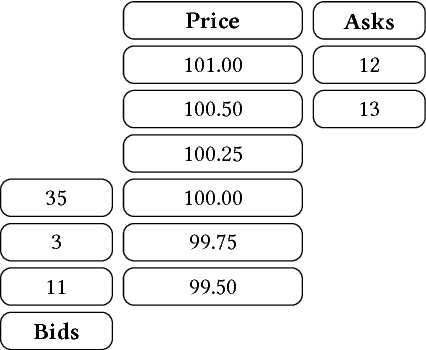
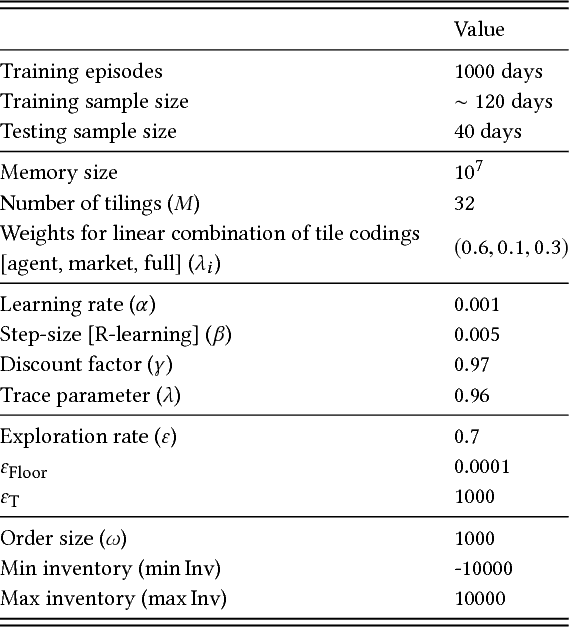
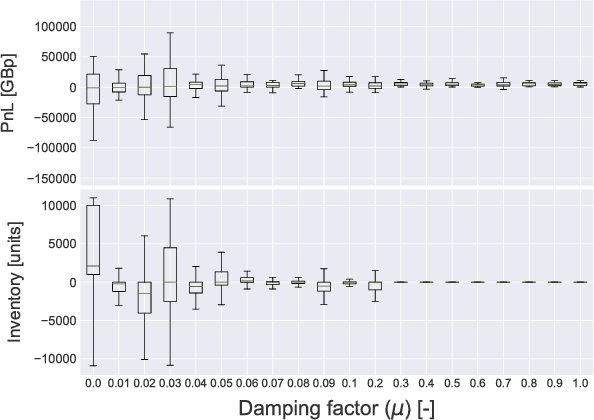
Market making is a fundamental trading problem in which an agent provides liquidity by continually offering to buy and sell a security. The problem is challenging due to inventory risk, the risk of accumulating an unfavourable position and ultimately losing money. In this paper, we develop a high-fidelity simulation of limit order book markets, and use it to design a market making agent using temporal-difference reinforcement learning. We use a linear combination of tile codings as a value function approximator, and design a custom reward function that controls inventory risk. We demonstrate the effectiveness of our approach by showing that our agent outperforms both simple benchmark strategies and a recent online learning approach from the literature.