The Complexity of Splitting Necklaces and Bisecting Ham Sandwiches
Paper and Code
Nov 05, 2018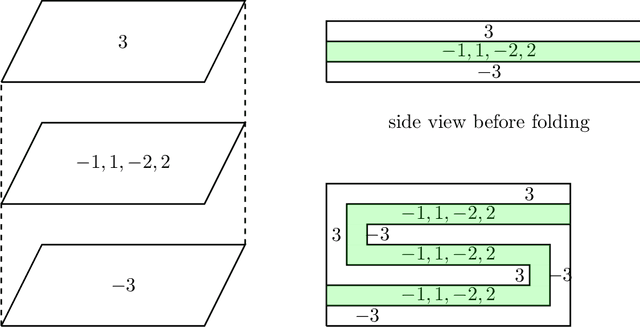
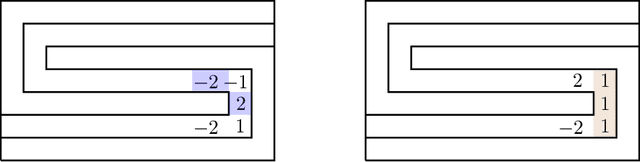
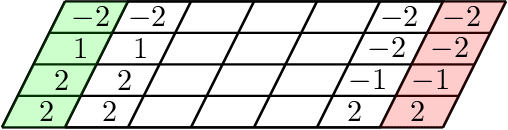
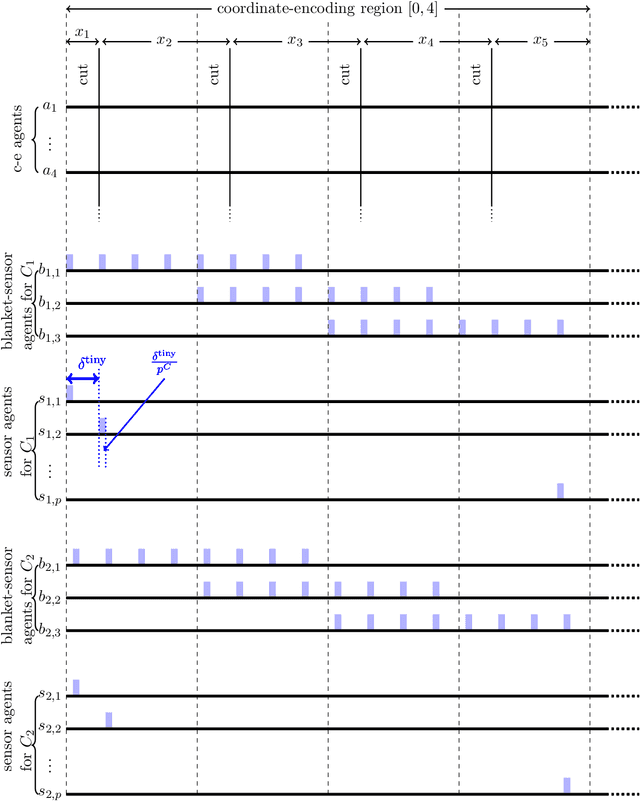
We resolve the computational complexity of two problems known as NECKLACE-SPLITTING and DISCRETE HAM SANDWICH, showing that they are PPA-complete. For NECKLACE SPLITTING, this result is specific to the important special case in which two thieves share the necklace. We do this via a PPA-completeness result for an approximate version of the CONSENSUS-HALVING problem, strengthening our recent result that the problem is PPA-complete for inverse-exponential precision. At the heart of our construction is a smooth embedding of the high-dimensional M\"obius strip in the CONSENSUS-HALVING problem. These results settle the status of PPA as a class that captures the complexity of "natural" problems whose definitions do not incorporate a circuit.
* 58 pages, 20 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge