Osman Yağan
Pairwise Elimination with Instance-Dependent Guarantees for Bandits with Cost Subsidy
Jan 17, 2025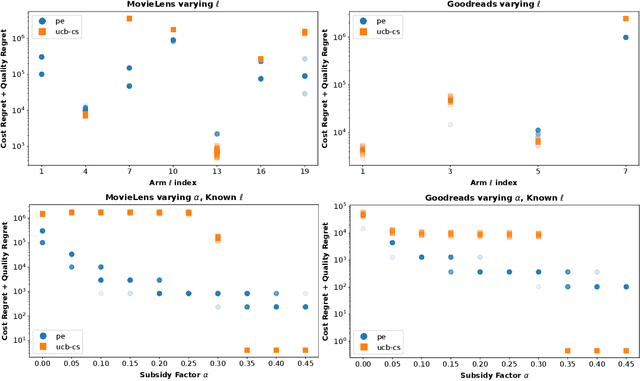

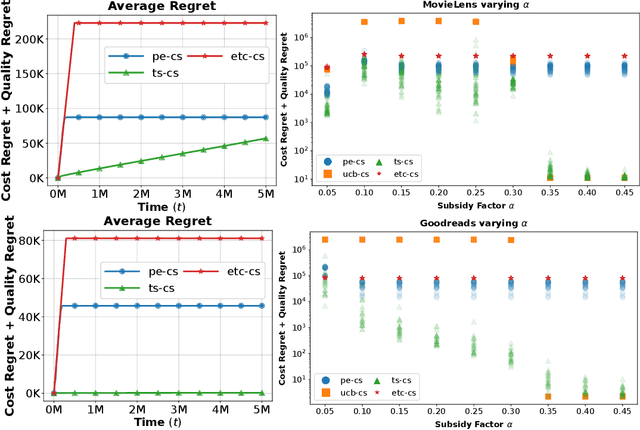

Abstract:Multi-armed bandits (MAB) are commonly used in sequential online decision-making when the reward of each decision is an unknown random variable. In practice however, the typical goal of maximizing total reward may be less important than minimizing the total cost of the decisions taken, subject to a reward constraint. For example, we may seek to make decisions that have at least the reward of a reference ``default'' decision, with as low a cost as possible. This problem was recently introduced in the Multi-Armed Bandits with Cost Subsidy (MAB-CS) framework. MAB-CS is broadly applicable to problem domains where a primary metric (cost) is constrained by a secondary metric (reward), and the rewards are unknown. In our work, we address variants of MAB-CS including ones with reward constrained by the reward of a known reference arm or by the subsidized best reward. We introduce the Pairwise-Elimination (PE) algorithm for the known reference arm variant and generalize PE to PE-CS for the subsidized best reward variant. Our instance-dependent analysis of PE and PE-CS reveals that both algorithms have an order-wise logarithmic upper bound on Cost and Quality Regret, making our policies the first with such a guarantee. Moreover, by comparing our upper and lower bound results we establish that PE is order-optimal for all known reference arm problem instances. Finally, experiments are conducted using the MovieLens 25M and Goodreads datasets for both PE and PE-CS revealing the effectiveness of PE and the superior balance between performance and reliability offered by PE-CS compared to baselines from the literature.
Best-Arm Identification in Correlated Multi-Armed Bandits
Sep 10, 2021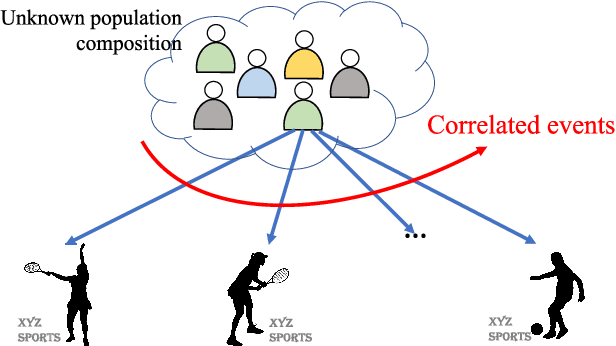
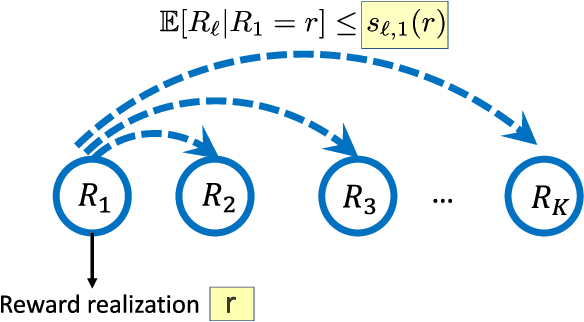
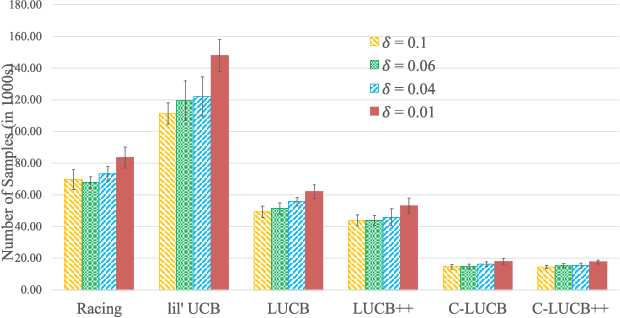
Abstract:In this paper we consider the problem of best-arm identification in multi-armed bandits in the fixed confidence setting, where the goal is to identify, with probability $1-\delta$ for some $\delta>0$, the arm with the highest mean reward in minimum possible samples from the set of arms $\mathcal{K}$. Most existing best-arm identification algorithms and analyses operate under the assumption that the rewards corresponding to different arms are independent of each other. We propose a novel correlated bandit framework that captures domain knowledge about correlation between arms in the form of upper bounds on expected conditional reward of an arm, given a reward realization from another arm. Our proposed algorithm C-LUCB, which generalizes the LUCB algorithm utilizes this partial knowledge of correlations to sharply reduce the sample complexity of best-arm identification. More interestingly, we show that the total samples obtained by C-LUCB are of the form $\mathcal{O}\left(\sum_{k \in \mathcal{C}} \log\left(\frac{1}{\delta}\right)\right)$ as opposed to the typical $\mathcal{O}\left(\sum_{k \in \mathcal{K}} \log\left(\frac{1}{\delta}\right)\right)$ samples required in the independent reward setting. The improvement comes, as the $\mathcal{O}(\log(1/\delta))$ term is summed only for the set of competitive arms $\mathcal{C}$, which is a subset of the original set of arms $\mathcal{K}$. The size of the set $\mathcal{C}$, depending on the problem setting, can be as small as $2$, and hence using C-LUCB in the correlated bandits setting can lead to significant performance improvements. Our theoretical findings are supported by experiments on the Movielens and Goodreads recommendation datasets.
Bandit-based Communication-Efficient Client Selection Strategies for Federated Learning
Dec 14, 2020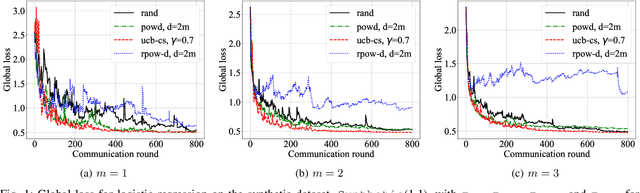
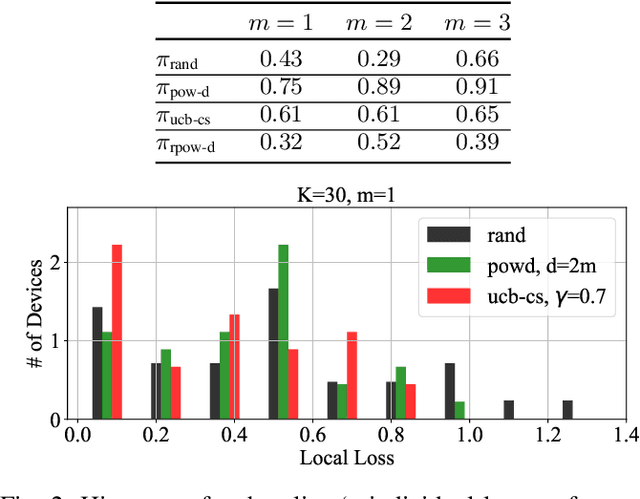
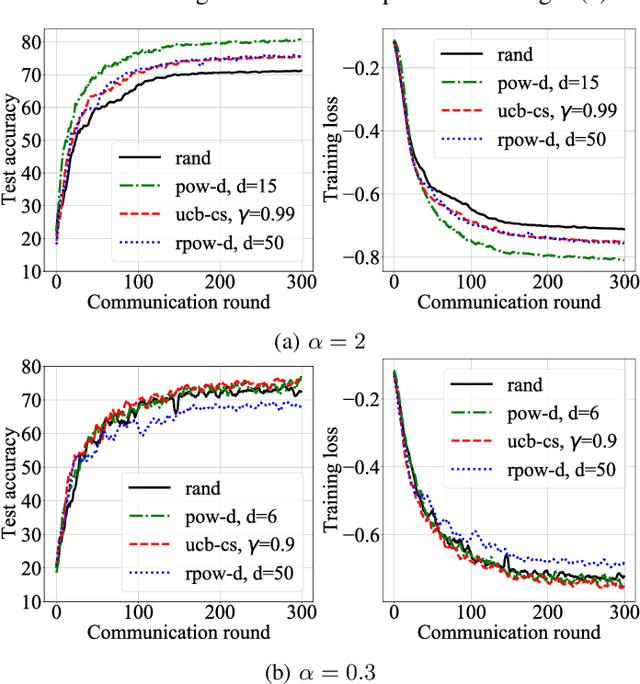
Abstract:Due to communication constraints and intermittent client availability in federated learning, only a subset of clients can participate in each training round. While most prior works assume uniform and unbiased client selection, recent work on biased client selection has shown that selecting clients with higher local losses can improve error convergence speed. However, previously proposed biased selection strategies either require additional communication cost for evaluating the exact local loss or utilize stale local loss, which can even make the model diverge. In this paper, we present a bandit-based communication-efficient client selection strategy UCB-CS that achieves faster convergence with lower communication overhead. We also demonstrate how client selection can be used to improve fairness.
Multi-Armed Bandits with Correlated Arms
Dec 03, 2019

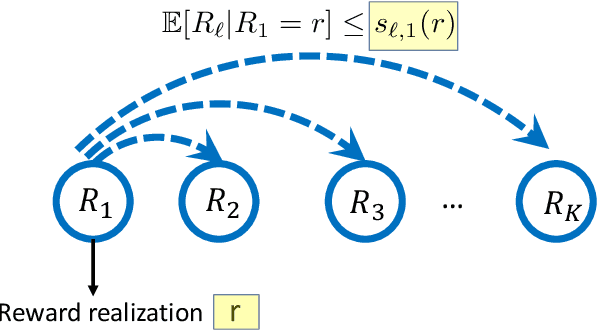

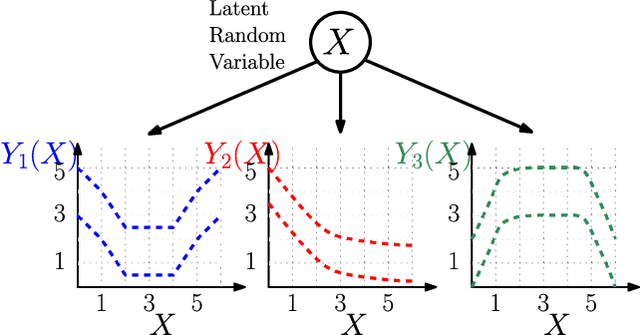
Abstract:We consider a multi-armed bandit framework where the rewards obtained by pulling different arms are correlated. The correlation information is captured in terms of \textit{pseudo-rewards}, which are bounds on the rewards on the other arm given a reward realization and can capture many general correlation structures. We leverage these pseudo-rewards to design a novel approach that extends any classical bandit algorithm to the correlated multi-armed bandit setting studied in the framework. In each round, our proposed C-Bandit algorithm identifies some arms as empirically non-competitive, and avoids exploring them for that round. Through a unified regret analysis of the proposed C-Bandit algorithm, we show that C-UCB and C-TS (the correlated bandit versions of Upper-confidence-bound and Thompson sampling) pull certain arms called non-competitive arms, only O(1) times. As a result, we effectively reduce a $K$-armed bandit problem to a $C+1$-armed bandit problem, where $C$ is the number of competitive arms, as only $C$ sub-optimal arms are pulled O(log T) times. In many practical scenarios, $C$ can be zero due to which our proposed C-Bandit algorithms achieve bounded regret. In the special case where rewards are correlated through a latent random variable $X$, we give a regret lower bound that shows that bounded regret is possible only when $C = 0$. In addition to simulations, we validate the proposed algorithms via experiments on two real-world recommendation datasets, movielens and goodreads, and show that C-UCB and C-TS significantly outperform classical bandit algorithms.
Exploiting Correlation in Finite-Armed Structured Bandits
Oct 18, 2018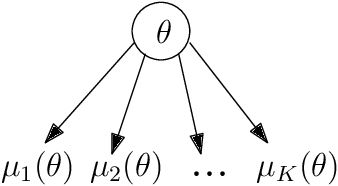
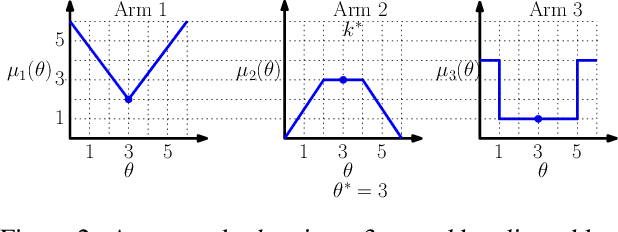
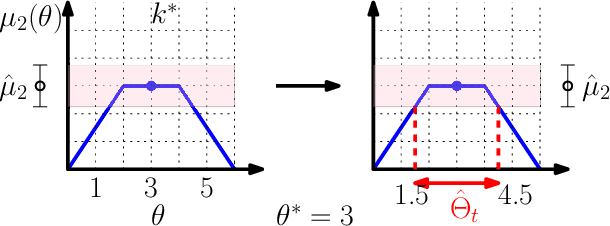
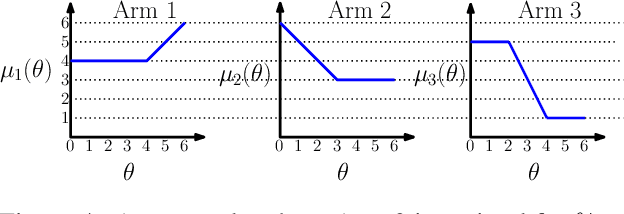
Abstract:We consider a correlated multi-armed bandit problem in which rewards of arms are correlated through a hidden parameter. Our approach exploits the correlation among arms to identify some arms as sub-optimal and pulls them only $\mathcal{O}(1)$ times. This results in significant reduction in cumulative regret, and in fact our algorithm achieves bounded (i.e., $\mathcal{O}(1)$) regret whenever possible; explicit conditions needed for bounded regret to be possible are also provided by analyzing regret lower bounds. We propose several variants of our approach that generalize classical bandit algorithms such as UCB, Thompson sampling, KL-UCB to the structured bandit setting, and empirically demonstrate their superiority via simulations.
Correlated Multi-armed Bandits with a Latent Random Source
Aug 17, 2018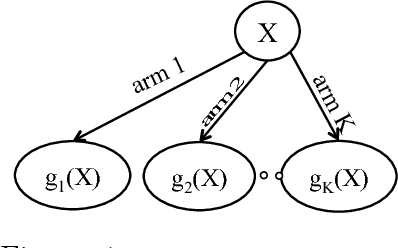
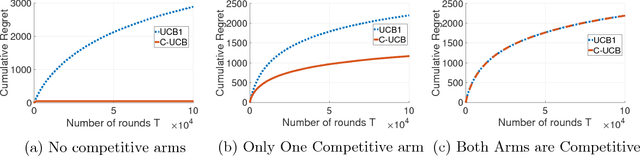
Abstract:We consider a novel multi-armed bandit framework where the rewards obtained by pulling the arms are functions of a common latent random variable. The correlation between arms due to the common random source can be used to design a generalized upper-confidence-bound (UCB) algorithm that identifies certain arms as $non-competitive$, and avoids exploring them. As a result, we reduce a $K$-armed bandit problem to a $C+1$-armed problem, where $C+1$ includes the best arm and $C$ $competitive$ arms. Our regret analysis shows that the competitive arms need to be pulled $\mathcal{O}(\log T)$ times, while the non-competitive arms are pulled only $\mathcal{O}(1)$ times. As a result, there are regimes where our algorithm achieves a $\mathcal{O}(1)$ regret as opposed to the typical logarithmic regret scaling of multi-armed bandit algorithms. We also evaluate lower bounds on the expected regret and prove that our correlated-UCB algorithm is order-wise optimal.
Active Distribution Learning from Indirect Samples
Aug 16, 2018



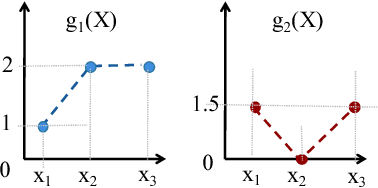
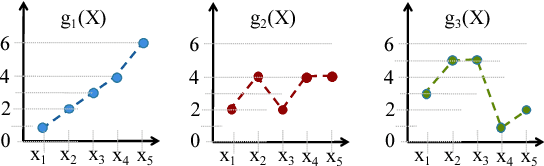
Abstract:This paper studies the problem of {\em learning} the probability distribution $P_X$ of a discrete random variable $X$ using indirect and sequential samples. At each time step, we choose one of the possible $K$ functions, $g_1, \ldots, g_K$ and observe the corresponding sample $g_i(X)$. The goal is to estimate the probability distribution of $X$ by using a minimum number of such sequential samples. This problem has several real-world applications including inference under non-precise information and privacy-preserving statistical estimation. We establish necessary and sufficient conditions on the functions $g_1, \ldots, g_K$ under which asymptotically consistent estimation is possible. We also derive lower bounds on the estimation error as a function of total samples and show that it is order-wise achievable. Leveraging these results, we propose an iterative algorithm that i) chooses the function to observe at each step based on past observations; and ii) combines the obtained samples to estimate $p_X$. The performance of this algorithm is investigated numerically under various scenarios, and shown to outperform baseline approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge