Best-Arm Identification in Correlated Multi-Armed Bandits
Paper and Code
Sep 10, 2021
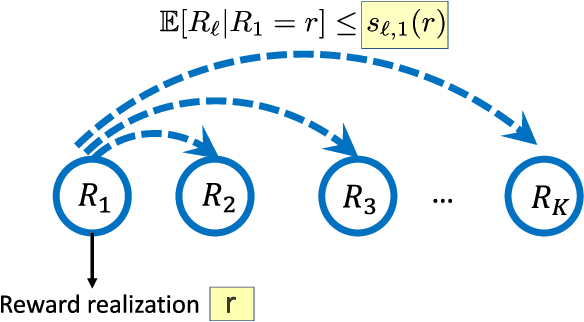
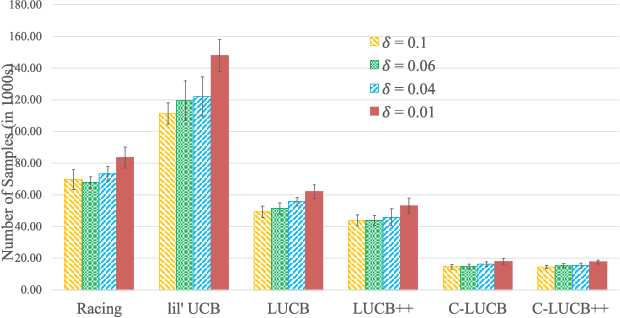
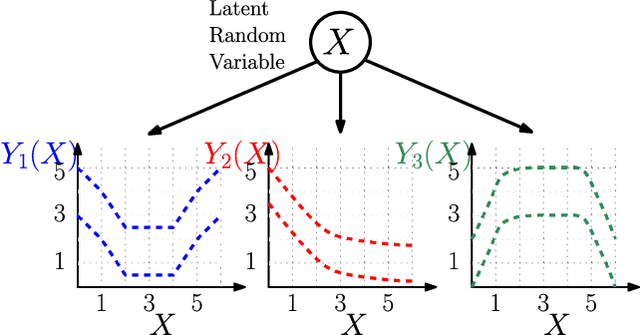
In this paper we consider the problem of best-arm identification in multi-armed bandits in the fixed confidence setting, where the goal is to identify, with probability $1-\delta$ for some $\delta>0$, the arm with the highest mean reward in minimum possible samples from the set of arms $\mathcal{K}$. Most existing best-arm identification algorithms and analyses operate under the assumption that the rewards corresponding to different arms are independent of each other. We propose a novel correlated bandit framework that captures domain knowledge about correlation between arms in the form of upper bounds on expected conditional reward of an arm, given a reward realization from another arm. Our proposed algorithm C-LUCB, which generalizes the LUCB algorithm utilizes this partial knowledge of correlations to sharply reduce the sample complexity of best-arm identification. More interestingly, we show that the total samples obtained by C-LUCB are of the form $\mathcal{O}\left(\sum_{k \in \mathcal{C}} \log\left(\frac{1}{\delta}\right)\right)$ as opposed to the typical $\mathcal{O}\left(\sum_{k \in \mathcal{K}} \log\left(\frac{1}{\delta}\right)\right)$ samples required in the independent reward setting. The improvement comes, as the $\mathcal{O}(\log(1/\delta))$ term is summed only for the set of competitive arms $\mathcal{C}$, which is a subset of the original set of arms $\mathcal{K}$. The size of the set $\mathcal{C}$, depending on the problem setting, can be as small as $2$, and hence using C-LUCB in the correlated bandits setting can lead to significant performance improvements. Our theoretical findings are supported by experiments on the Movielens and Goodreads recommendation datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge