Correlated Multi-armed Bandits with a Latent Random Source

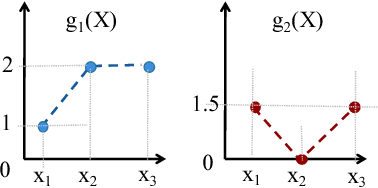
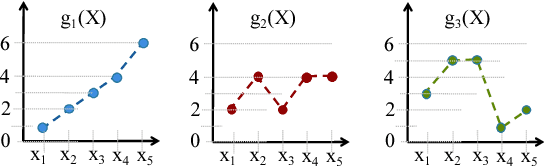
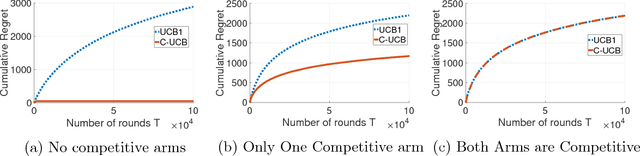
We consider a novel multi-armed bandit framework where the rewards obtained by pulling the arms are functions of a common latent random variable. The correlation between arms due to the common random source can be used to design a generalized upper-confidence-bound (UCB) algorithm that identifies certain arms as $non-competitive$, and avoids exploring them. As a result, we reduce a $K$-armed bandit problem to a $C+1$-armed problem, where $C+1$ includes the best arm and $C$ $competitive$ arms. Our regret analysis shows that the competitive arms need to be pulled $\mathcal{O}(\log T)$ times, while the non-competitive arms are pulled only $\mathcal{O}(1)$ times. As a result, there are regimes where our algorithm achieves a $\mathcal{O}(1)$ regret as opposed to the typical logarithmic regret scaling of multi-armed bandit algorithms. We also evaluate lower bounds on the expected regret and prove that our correlated-UCB algorithm is order-wise optimal.