Multi-Armed Bandits with Correlated Arms

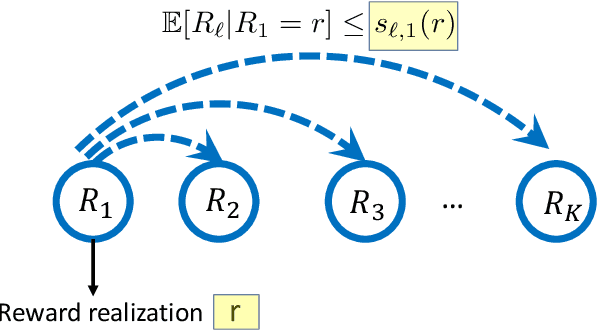
We consider a multi-armed bandit framework where the rewards obtained by pulling different arms are correlated. The correlation information is captured in terms of \textit{pseudo-rewards}, which are bounds on the rewards on the other arm given a reward realization and can capture many general correlation structures. We leverage these pseudo-rewards to design a novel approach that extends any classical bandit algorithm to the correlated multi-armed bandit setting studied in the framework. In each round, our proposed C-Bandit algorithm identifies some arms as empirically non-competitive, and avoids exploring them for that round. Through a unified regret analysis of the proposed C-Bandit algorithm, we show that C-UCB and C-TS (the correlated bandit versions of Upper-confidence-bound and Thompson sampling) pull certain arms called non-competitive arms, only O(1) times. As a result, we effectively reduce a $K$-armed bandit problem to a $C+1$-armed bandit problem, where $C$ is the number of competitive arms, as only $C$ sub-optimal arms are pulled O(log T) times. In many practical scenarios, $C$ can be zero due to which our proposed C-Bandit algorithms achieve bounded regret. In the special case where rewards are correlated through a latent random variable $X$, we give a regret lower bound that shows that bounded regret is possible only when $C = 0$. In addition to simulations, we validate the proposed algorithms via experiments on two real-world recommendation datasets, movielens and goodreads, and show that C-UCB and C-TS significantly outperform classical bandit algorithms.