Exploiting Correlation in Finite-Armed Structured Bandits

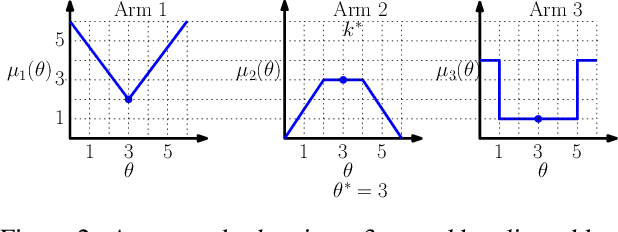
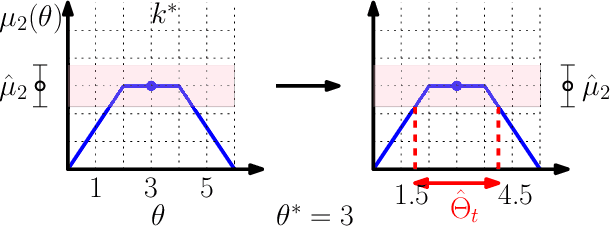
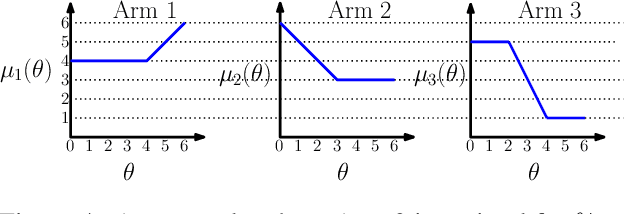
We consider a correlated multi-armed bandit problem in which rewards of arms are correlated through a hidden parameter. Our approach exploits the correlation among arms to identify some arms as sub-optimal and pulls them only $\mathcal{O}(1)$ times. This results in significant reduction in cumulative regret, and in fact our algorithm achieves bounded (i.e., $\mathcal{O}(1)$) regret whenever possible; explicit conditions needed for bounded regret to be possible are also provided by analyzing regret lower bounds. We propose several variants of our approach that generalize classical bandit algorithms such as UCB, Thompson sampling, KL-UCB to the structured bandit setting, and empirically demonstrate their superiority via simulations.