Statistical Inference with Limited Memory: A Survey

The problem of statistical inference in its various forms has been the subject of decades-long extensive research. Most of the effort has been focused on characterizing the behavior as a function of the number of available samples, with far less attention given to the effect of memory limitations on performance. Recently, this latter topic has drawn much interest in the engineering and computer science literature. In this survey paper, we attempt to review the state-of-the-art of statistical inference under memory constraints in several canonical problems, including hypothesis testing, parameter estimation, and distribution property testing/estimation. We discuss the main results in this developing field, and by identifying recurrent themes, we extract some fundamental building blocks for algorithmic construction, as well as useful techniques for lower bound derivations.

Batches Stabilize the Minimum Norm Risk in High Dimensional Overparameterized Linear Regression

Learning algorithms that divide the data into batches are prevalent in many machine-learning applications, typically offering useful trade-offs between computational efficiency and performance. In this paper, we examine the benefits of batch-partitioning through the lens of a minimum-norm overparameterized linear regression model with isotropic Gaussian features. We suggest a natural small-batch version of the minimum-norm estimator, and derive an upper bound on its quadratic risk, showing it is inversely proportional to the noise level as well as to the overparameterization ratio, for the optimal choice of batch size. In contrast to minimum-norm, our estimator admits a stable risk behavior that is monotonically increasing in the overparameterization ratio, eliminating both the blowup at the interpolation point and the double-descent phenomenon. Interestingly, we observe that this implicit regularization offered by the batch partition is partially explained by feature overlap between the batches. Our bound is derived via a novel combination of techniques, in particular normal approximation in the Wasserstein metric of noisy projections over random subspaces.

Planted Bipartite Graph Detection

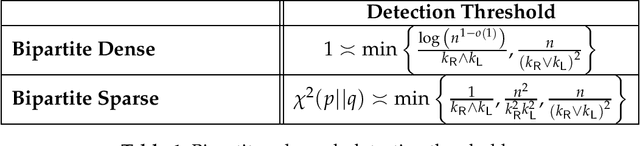
We consider the task of detecting a hidden bipartite subgraph in a given random graph. Specifically, under the null hypothesis, the graph is a realization of an Erd\H{o}s-R\'{e}nyi random graph over $n$ vertices with edge density $q$. Under the alternative, there exists a planted $k_{\mathsf{R}} \times k_{\mathsf{L}}$ bipartite subgraph with edge density $p>q$. We derive asymptotically tight upper and lower bounds for this detection problem in both the dense regime, where $q,p = \Theta\left(1\right)$, and the sparse regime where $q,p = \Theta\left(n^{-\alpha}\right), \alpha \in \left(0,2\right]$. Moreover, we consider a variant of the above problem, where one can only observe a relatively small part of the graph, by using at most $\mathsf{Q}$ edge queries. For this problem, we derive upper and lower bounds in both the dense and sparse regimes.

Learning User Preferences in Non-Stationary Environments

Recommendation systems often use online collaborative filtering (CF) algorithms to identify items a given user likes over time, based on ratings that this user and a large number of other users have provided in the past. This problem has been studied extensively when users' preferences do not change over time (static case); an assumption that is often violated in practical settings. In this paper, we introduce a novel model for online non-stationary recommendation systems which allows for temporal uncertainties in the users' preferences. For this model, we propose a user-based CF algorithm, and provide a theoretical analysis of its achievable reward. Compared to related non-stationary multi-armed bandit literature, the main fundamental difficulty in our model lies in the fact that variations in the preferences of a certain user may affect the recommendations for other users severely. We also test our algorithm over real-world datasets, showing its effectiveness in real-world applications. One of the main surprising observations in our experiments is the fact our algorithm outperforms other static algorithms even when preferences do not change over time. This hints toward the general conclusion that in practice, dynamic algorithms, such as the one we propose, might be beneficial even in stationary environments.

Simple Modulo can Significantly Outperform Deep Learning-based Deepcode

Deepcode (H.Kim et al.2018) is a recently suggested Deep Learning-based scheme for communication over the AWGN channel with noisy feedback, claimed to be superior to all previous schemes in the literature. Deepcode's use of nonlinear coding (via Deep Learning) has been inspired by known shortcomings (Y.-H. Kim et al 2007) of linear feedback schemes. In 2014, we presented a nonlinear feedback coding scheme based on a combination of the classical SK scheme and modulo-arithmetic, using a small number of elementary operations without any type of neural network. This Modulo-SK scheme has been omitted from the performance comparisons made in the Deepcode paper, due to its use of common randomness (dither), and in a later version since it was incorrectly interpreted as a variable-length coding scheme. However, the dither in Modulo-SK was used only for the standard purpose of tractable performance analysis, and is not required in practice. In this short note, we show that a fully-deterministic Modulo-SK (without dithering) can outperform Deepcode. For example, to attain an error probability of 10^(-4) at rate 1/3 Modulo-SK requires 3dB less feedback SNR than Deepcode. To attain an error probability of 10^(-6) with noiseless feedback, Deepcode requires 150 rounds of communication, whereas Modulo-SK requires only 15 rounds, even if the feedback is noisy (with 27dB SNR). We further address the numerical stability issues of the original SK scheme reported in the Deepcode paper, and explain how they can be avoided. We augment this report with an online-available, fully-functional Matlab simulation for both the classical and Modulo-SK schemes. Finally, note that Modulo-SK is by no means claimed to be the best possible solution; in particular, using deep learning in conjunction with modulo-arithmetic might lead to better designs, and remains a fascinating direction for future research.

Sharp Thresholds of the Information Cascade Fragility Under a Mismatched Model

We analyze a sequential decision making model in which decision makers (or, players) take their decisions based on their own private information as well as the actions of previous decision makers. Such decision making processes often lead to what is known as the \emph{information cascade} or \emph{herding} phenomenon. Specifically, a cascade develops when it seems rational for some players to abandon their own private information and imitate the actions of earlier players. The risk, however, is that if the initial decisions were wrong, then the whole cascade will be wrong. Nonetheless, information cascade are known to be fragile: there exists a sequence of \emph{revealing} probabilities $\{p_{\ell}\}_{\ell\geq1}$, such that if with probability $p_{\ell}$ player $\ell$ ignores the decisions of previous players, and rely on his private information only, then wrong cascades can be avoided. Previous related papers which study the fragility of information cascades always assume that the revealing probabilities are known to all players perfectly, which might be unrealistic in practice. Accordingly, in this paper we study a mismatch model where players believe that the revealing probabilities are $\{q_\ell\}_{\ell\in\mathbb{N}}$ when they truly are $\{p_\ell\}_{\ell\in\mathbb{N}}$, and study the effect of this mismatch on information cascades. We consider both adversarial and probabilistic sequential decision making models, and derive closed-form expressions for the optimal learning rates at which the error probability associated with a certain decision maker goes to zero. We prove several novel phase transitions in the behaviour of the asymptotic learning rate.

Communication Complexity of Estimating Correlations

We characterize the communication complexity of the following distributed estimation problem. Alice and Bob observe infinitely many iid copies of $\rho$-correlated unit-variance (Gaussian or $\pm1$ binary) random variables, with unknown $\rho\in[-1,1]$. By interactively exchanging $k$ bits, Bob wants to produce an estimate $\hat\rho$ of $\rho$. We show that the best possible performance (optimized over interaction protocol $\Pi$ and estimator $\hat \rho$) satisfies $\inf_{\Pi,\hat\rho}\sup_\rho \mathbb{E} [|\rho-\hat\rho|^2] = \Theta(\tfrac{1}{k})$. Furthermore, we show that the best possible unbiased estimator achieves performance of $1+o(1)\over {2k\ln 2}$. Curiously, thus, restricting communication to $k$ bits results in (order-wise) similar minimax estimation error as restricting to $k$ samples. Our results also imply an $\Omega(n)$ lower bound on the information complexity of the Gap-Hamming problem, for which we show a direct information-theoretic proof. Notably, the protocol achieving (almost) optimal performance is one-way (non-interactive). For one-way protocols we also prove the $\Omega(\tfrac{1}{k})$ bound even when $\rho$ is restricted to any small open sub-interval of $[-1,1]$ (i.e. a local minimax lower bound). %We do not know if this local behavior remains true in the interactive setting. Our proof techniques rely on symmetric strong data-processing inequalities, various tensorization techniques from information-theoretic interactive common-randomness extraction, and (for the local lower bound) on the Otto-Villani estimate for the Wasserstein-continuity of trajectories of the Ornstein-Uhlenbeck semigroup.

Distributed Estimation of Gaussian Correlations

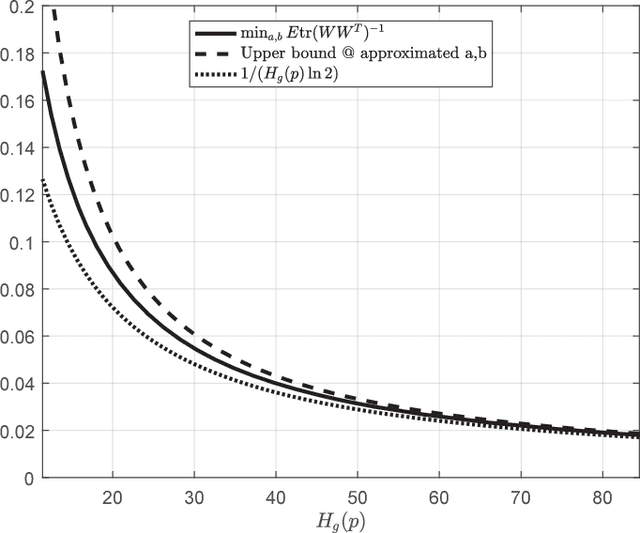
We study a distributed estimation problem in which two remotely located parties, Alice and Bob, observe an unlimited number of i.i.d. samples corresponding to two different parts of a random vector. Alice can send $k$ bits on average to Bob, who in turn wants to estimate the cross-correlation matrix between the two parts of the vector. In the case where the parties observe jointly Gaussian scalar random variables with an unknown correlation $\rho$, we obtain two constructive and simple unbiased estimators attaining a variance of $(1-\rho^2)/(2k\ln 2)$, which coincides with a known but non-constructive random coding result of Zhang and Berger. We extend our approach to the vector Gaussian case, which has not been treated before, and construct an estimator that is uniformly better than the scalar estimator applied separately to each of the correlations. We then show that the Gaussian performance can essentially be attained even when the distribution is completely unknown. This in particular implies that in the general problem of distributed correlation estimation, the variance can decay at least as $O(1/k)$ with the number of transmitted bits. This behavior, however, is not tight: we give an example of a rich family of distributions for which local samples reveal essentially nothing about the correlations, and where a slightly modified estimator attains a variance of $2^{-\Omega(k)}$.