Asaf Rotenberg
Planted Bipartite Graph Detection
Feb 07, 2023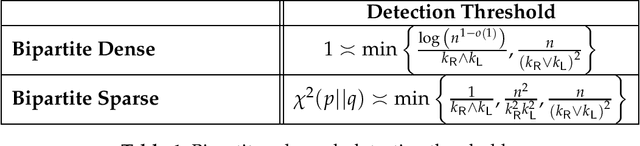



Abstract:We consider the task of detecting a hidden bipartite subgraph in a given random graph. Specifically, under the null hypothesis, the graph is a realization of an Erd\H{o}s-R\'{e}nyi random graph over $n$ vertices with edge density $q$. Under the alternative, there exists a planted $k_{\mathsf{R}} \times k_{\mathsf{L}}$ bipartite subgraph with edge density $p>q$. We derive asymptotically tight upper and lower bounds for this detection problem in both the dense regime, where $q,p = \Theta\left(1\right)$, and the sparse regime where $q,p = \Theta\left(n^{-\alpha}\right), \alpha \in \left(0,2\right]$. Moreover, we consider a variant of the above problem, where one can only observe a relatively small part of the graph, by using at most $\mathsf{Q}$ edge queries. For this problem, we derive upper and lower bounds in both the dense and sparse regimes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge