Communication Complexity of Estimating Correlations

We characterize the communication complexity of the following distributed estimation problem. Alice and Bob observe infinitely many iid copies of $\rho$-correlated unit-variance (Gaussian or $\pm1$ binary) random variables, with unknown $\rho\in[-1,1]$. By interactively exchanging $k$ bits, Bob wants to produce an estimate $\hat\rho$ of $\rho$. We show that the best possible performance (optimized over interaction protocol $\Pi$ and estimator $\hat \rho$) satisfies $\inf_{\Pi,\hat\rho}\sup_\rho \mathbb{E} [|\rho-\hat\rho|^2] = \Theta(\tfrac{1}{k})$. Furthermore, we show that the best possible unbiased estimator achieves performance of $1+o(1)\over {2k\ln 2}$. Curiously, thus, restricting communication to $k$ bits results in (order-wise) similar minimax estimation error as restricting to $k$ samples. Our results also imply an $\Omega(n)$ lower bound on the information complexity of the Gap-Hamming problem, for which we show a direct information-theoretic proof. Notably, the protocol achieving (almost) optimal performance is one-way (non-interactive). For one-way protocols we also prove the $\Omega(\tfrac{1}{k})$ bound even when $\rho$ is restricted to any small open sub-interval of $[-1,1]$ (i.e. a local minimax lower bound). %We do not know if this local behavior remains true in the interactive setting. Our proof techniques rely on symmetric strong data-processing inequalities, various tensorization techniques from information-theoretic interactive common-randomness extraction, and (for the local lower bound) on the Otto-Villani estimate for the Wasserstein-continuity of trajectories of the Ornstein-Uhlenbeck semigroup.

Distributed Estimation of Gaussian Correlations

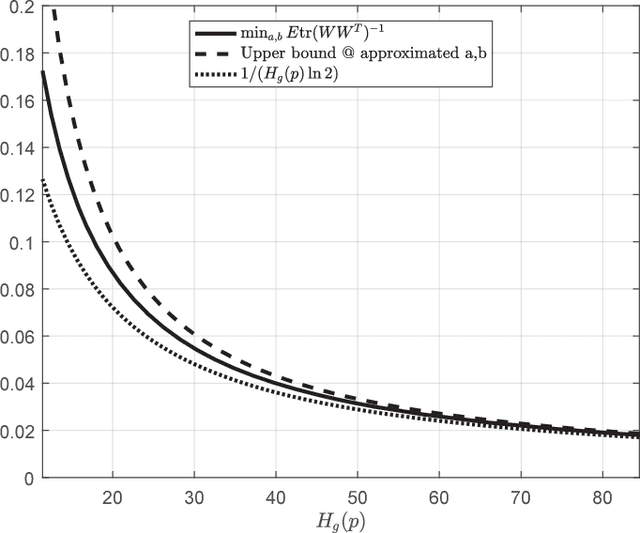
We study a distributed estimation problem in which two remotely located parties, Alice and Bob, observe an unlimited number of i.i.d. samples corresponding to two different parts of a random vector. Alice can send $k$ bits on average to Bob, who in turn wants to estimate the cross-correlation matrix between the two parts of the vector. In the case where the parties observe jointly Gaussian scalar random variables with an unknown correlation $\rho$, we obtain two constructive and simple unbiased estimators attaining a variance of $(1-\rho^2)/(2k\ln 2)$, which coincides with a known but non-constructive random coding result of Zhang and Berger. We extend our approach to the vector Gaussian case, which has not been treated before, and construct an estimator that is uniformly better than the scalar estimator applied separately to each of the correlations. We then show that the Gaussian performance can essentially be attained even when the distribution is completely unknown. This in particular implies that in the general problem of distributed correlation estimation, the variance can decay at least as $O(1/k)$ with the number of transmitted bits. This behavior, however, is not tight: we give an example of a rich family of distributions for which local samples reveal essentially nothing about the correlations, and where a slightly modified estimator attains a variance of $2^{-\Omega(k)}$.