DHIL-GT: Scalable Graph Transformer with Decoupled Hierarchy Labeling

Graph Transformer (GT) has recently emerged as a promising neural network architecture for learning graph-structured data. However, its global attention mechanism with quadratic complexity concerning the graph scale prevents wider application to large graphs. While current methods attempt to enhance GT scalability by altering model architecture or encoding hierarchical graph data, our analysis reveals that these models still suffer from the computational bottleneck related to graph-scale operations. In this work, we target the GT scalability issue and propose DHIL-GT, a scalable Graph Transformer that simplifies network learning by fully decoupling the graph computation to a separate stage in advance. DHIL-GT effectively retrieves hierarchical information by exploiting the graph labeling technique, as we show that the graph label hierarchy is more informative than plain adjacency by offering global connections while promoting locality, and is particularly suitable for handling complex graph patterns such as heterophily. We further design subgraph sampling and positional encoding schemes for precomputing model input on top of graph labels in an end-to-end manner. The training stage thus favorably removes graph-related computations, leading to ideal mini-batch capability and GPU utilization. Notably, the precomputation and training processes of DHIL-GT achieve complexities linear to the number of graph edges and nodes, respectively. Extensive experiments demonstrate that DHIL-GT is efficient in terms of computational boost and mini-batch capability over existing scalable Graph Transformer designs on large-scale benchmarks, while achieving top-tier effectiveness on both homophilous and heterophilous graphs.

Benchmarking Spectral Graph Neural Networks: A Comprehensive Study on Effectiveness and Efficiency

With the recent advancements in graph neural networks (GNNs), spectral GNNs have received increasing popularity by virtue of their specialty in capturing graph signals in the frequency domain, demonstrating promising capability in specific tasks. However, few systematic studies have been conducted on assessing their spectral characteristics. This emerging family of models also varies in terms of designs and settings, leading to difficulties in comparing their performance and deciding on the suitable model for specific scenarios, especially for large-scale tasks. In this work, we extensively benchmark spectral GNNs with a focus on the frequency perspective. We analyze and categorize over 30 GNNs with 27 corresponding filters. Then, we implement these spectral models under a unified framework with dedicated graph computations and efficient training schemes. Thorough experiments are conducted on the spectral models with inclusive metrics on effectiveness and efficiency, offering practical guidelines on evaluating and selecting spectral GNNs with desirable performance. Our implementation enables application on larger graphs with comparable performance and less overhead, which is available at: https://github.com/gdmnl/Spectral-GNN-Benchmark.

Unifews: Unified Entry-Wise Sparsification for Efficient Graph Neural Network

Graph Neural Networks (GNNs) have shown promising performance in various graph learning tasks, but at the cost of resource-intensive computations. The primary overhead of GNN update stems from graph propagation and weight transformation, both involving operations on graph-scale matrices. Previous studies attempt to reduce the computational budget by leveraging graph-level or network-level sparsification techniques, resulting in downsized graph or weights. In this work, we propose Unifews, which unifies the two operations in an entry-wise manner considering individual matrix elements, and conducts joint edge-weight sparsification to enhance learning efficiency. The entry-wise design of Unifews enables adaptive compression across GNN layers with progressively increased sparsity, and is applicable to a variety of architectural designs with on-the-fly operation simplification. Theoretically, we establish a novel framework to characterize sparsified GNN learning in view of a graph optimization process, and prove that Unifews effectively approximates the learning objective with bounded error and reduced computational load. We conduct extensive experiments to evaluate the performance of our method in diverse settings. Unifews is advantageous in jointly removing more than 90% of edges and weight entries with comparable or better accuracy than baseline models. The sparsification offers remarkable efficiency improvements including 10-20x matrix operation reduction and up to 100x acceleration in graph propagation time for the largest graph at the billion-edge scale.

SIMGA: A Simple and Effective Heterophilous Graph Neural Network with Efficient Global Aggregation

Graph neural networks (GNNs) realize great success in graph learning but suffer from performance loss when meeting heterophily, i.e. neighboring nodes are dissimilar, due to their local and uniform aggregation. Existing attempts in incoorporating global aggregation for heterophilous GNNs usually require iteratively maintaining and updating full-graph information, which entails $\mathcal{O}(n^2)$ computation efficiency for a graph with $n$ nodes, leading to weak scalability to large graphs. In this paper, we propose SIMGA, a GNN structure integrating SimRank structural similarity measurement as global aggregation. The design of SIMGA is simple, yet it leads to promising results in both efficiency and effectiveness. The simplicity of SIMGA makes it the first heterophilous GNN model that can achieve a propagation efficiency near-linear to $n$. We theoretically demonstrate its effectiveness by treating SimRank as a new interpretation of GNN and prove that the aggregated node representation matrix has expected grouping effect. The performances of SIMGA are evaluated with 11 baselines on 12 benchmark datasets, usually achieving superior accuracy compared with the state-of-the-art models. Efficiency study reveals that SIMGA is up to 5$\times$ faster than the state-of-the-art method on the largest heterophily dataset pokec with over 30 million edges.

SCARA: Scalable Graph Neural Networks with Feature-Oriented Optimization

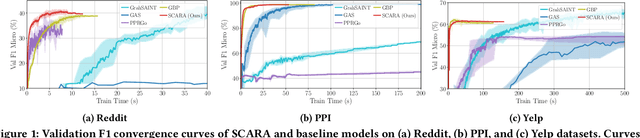
Recent advances in data processing have stimulated the demand for learning graphs of very large scales. Graph Neural Networks (GNNs), being an emerging and powerful approach in solving graph learning tasks, are known to be difficult to scale up. Most scalable models apply node-based techniques in simplifying the expensive graph message-passing propagation procedure of GNN. However, we find such acceleration insufficient when applied to million- or even billion-scale graphs. In this work, we propose SCARA, a scalable GNN with feature-oriented optimization for graph computation. SCARA efficiently computes graph embedding from node features, and further selects and reuses feature computation results to reduce overhead. Theoretical analysis indicates that our model achieves sub-linear time complexity with a guaranteed precision in propagation process as well as GNN training and inference. We conduct extensive experiments on various datasets to evaluate the efficacy and efficiency of SCARA. Performance comparison with baselines shows that SCARA can reach up to 100x graph propagation acceleration than current state-of-the-art methods with fast convergence and comparable accuracy. Most notably, it is efficient to process precomputation on the largest available billion-scale GNN dataset Papers100M (111M nodes, 1.6B edges) in 100 seconds.

Achieving Adversarial Robustness via Sparsity

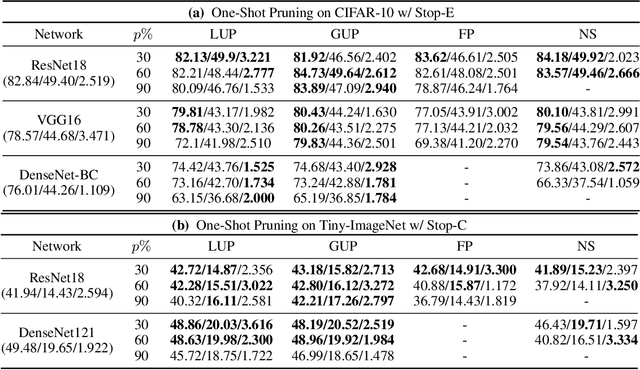
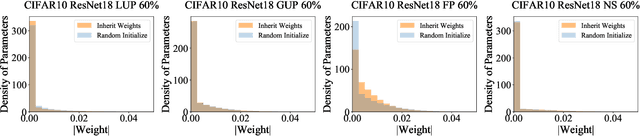
Network pruning has been known to produce compact models without much accuracy degradation. However, how the pruning process affects a network's robustness and the working mechanism behind remain unresolved. In this work, we theoretically prove that the sparsity of network weights is closely associated with model robustness. Through experiments on a variety of adversarial pruning methods, we find that weights sparsity will not hurt but improve robustness, where both weights inheritance from the lottery ticket and adversarial training improve model robustness in network pruning. Based on these findings, we propose a novel adversarial training method called inverse weights inheritance, which imposes sparse weights distribution on a large network by inheriting weights from a small network, thereby improving the robustness of the large network.