Potential and Perils of Large Language Models as Judges of Unstructured Textual Data

Rapid advancements in large language models have unlocked remarkable capabilities when it comes to processing and summarizing unstructured text data. This has implications for the analysis of rich, open-ended datasets, such as survey responses, where LLMs hold the promise of efficiently distilling key themes and sentiments. However, as organizations increasingly turn to these powerful AI systems to make sense of textual feedback, a critical question arises, can we trust LLMs to accurately represent the perspectives contained within these text based datasets? While LLMs excel at generating human-like summaries, there is a risk that their outputs may inadvertently diverge from the true substance of the original responses. Discrepancies between the LLM-generated outputs and the actual themes present in the data could lead to flawed decision-making, with far-reaching consequences for organizations. This research investigates the effectiveness of LLMs as judge models to evaluate the thematic alignment of summaries generated by other LLMs. We utilized an Anthropic Claude model to generate thematic summaries from open-ended survey responses, with Amazon's Titan Express, Nova Pro, and Meta's Llama serving as LLM judges. The LLM-as-judge approach was compared to human evaluations using Cohen's kappa, Spearman's rho, and Krippendorff's alpha, validating a scalable alternative to traditional human centric evaluation methods. Our findings reveal that while LLMs as judges offer a scalable solution comparable to human raters, humans may still excel at detecting subtle, context-specific nuances. This research contributes to the growing body of knowledge on AI assisted text analysis. We discuss limitations and provide recommendations for future research, emphasizing the need for careful consideration when generalizing LLM judge models across various contexts and use cases.

HR-MultiWOZ: A Task Oriented Dialogue Dataset for HR LLM Agent

Recent advancements in Large Language Models (LLMs) have been reshaping Natural Language Processing (NLP) task in several domains. Their use in the field of Human Resources (HR) has still room for expansions and could be beneficial for several time consuming tasks. Examples such as time-off submissions, medical claims filing, and access requests are noteworthy, but they are by no means the sole instances. However, the aforementioned developments must grapple with the pivotal challenge of constructing a high-quality training dataset. On one hand, most conversation datasets are solving problems for customers not employees. On the other hand, gathering conversations with HR could raise privacy concerns. To solve it, we introduce HR-Multiwoz, a fully-labeled dataset of 550 conversations spanning 10 HR domains to evaluate LLM Agent. Our work has the following contributions: (1) It is the first labeled open-sourced conversation dataset in the HR domain for NLP research. (2) It provides a detailed recipe for the data generation procedure along with data analysis and human evaluations. The data generation pipeline is transferable and can be easily adapted for labeled conversation data generation in other domains. (3) The proposed data-collection pipeline is mostly based on LLMs with minimal human involvement for annotation, which is time and cost-efficient.

On Regret-Optimal Learning in Decentralized Multi-player Multi-armed Bandits

We consider the problem of learning in single-player and multiplayer multiarmed bandit models. Bandit problems are classes of online learning problems that capture exploration versus exploitation tradeoffs. In a multiarmed bandit model, players can pick among many arms, and each play of an arm generates an i.i.d. reward from an unknown distribution. The objective is to design a policy that maximizes the expected reward over a time horizon for a single player setting and the sum of expected rewards for the multiplayer setting. In the multiplayer setting, arms may give different rewards to different players. There is no separate channel for coordination among the players. Any attempt at communication is costly and adds to regret. We propose two decentralizable policies, $\tt E^3$ ($\tt E$-$\tt cubed$) and $\tt E^3$-$\tt TS$, that can be used in both single player and multiplayer settings. These policies are shown to yield expected regret that grows at most as O($\log^{1+\epsilon} T$). It is well known that $\log T$ is the lower bound on the rate of growth of regret even in a centralized case. The proposed algorithms improve on prior work where regret grew at O($\log^2 T$). More fundamentally, these policies address the question of additional cost incurred in decentralized online learning, suggesting that there is at most an $\epsilon$-factor cost in terms of order of regret. This solves a problem of relevance in many domains and had been open for a while.

Decentralized Learning for Multi-player Multi-armed Bandits

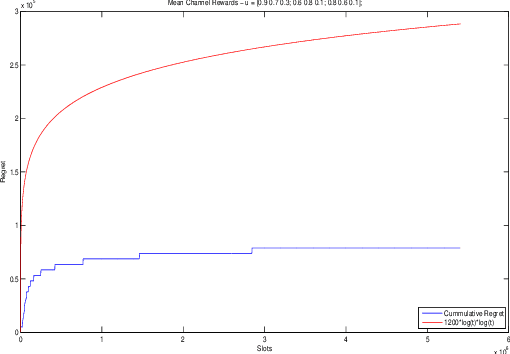
We consider the problem of distributed online learning with multiple players in multi-armed bandits (MAB) models. Each player can pick among multiple arms. When a player picks an arm, it gets a reward. We consider both i.i.d. reward model and Markovian reward model. In the i.i.d. model each arm is modelled as an i.i.d. process with an unknown distribution with an unknown mean. In the Markovian model, each arm is modelled as a finite, irreducible, aperiodic and reversible Markov chain with an unknown probability transition matrix and stationary distribution. The arms give different rewards to different players. If two players pick the same arm, there is a "collision", and neither of them get any reward. There is no dedicated control channel for coordination or communication among the players. Any other communication between the users is costly and will add to the regret. We propose an online index-based distributed learning policy called ${\tt dUCB_4}$ algorithm that trades off \textit{exploration v. exploitation} in the right way, and achieves expected regret that grows at most as near-$O(\log^2 T)$. The motivation comes from opportunistic spectrum access by multiple secondary users in cognitive radio networks wherein they must pick among various wireless channels that look different to different users. This is the first distributed learning algorithm for multi-player MABs to the best of our knowledge.