Decentralized Learning for Multi-player Multi-armed Bandits
Paper and Code
Jun 14, 2012
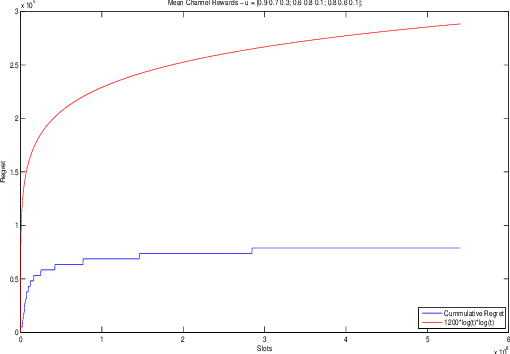
We consider the problem of distributed online learning with multiple players in multi-armed bandits (MAB) models. Each player can pick among multiple arms. When a player picks an arm, it gets a reward. We consider both i.i.d. reward model and Markovian reward model. In the i.i.d. model each arm is modelled as an i.i.d. process with an unknown distribution with an unknown mean. In the Markovian model, each arm is modelled as a finite, irreducible, aperiodic and reversible Markov chain with an unknown probability transition matrix and stationary distribution. The arms give different rewards to different players. If two players pick the same arm, there is a "collision", and neither of them get any reward. There is no dedicated control channel for coordination or communication among the players. Any other communication between the users is costly and will add to the regret. We propose an online index-based distributed learning policy called ${\tt dUCB_4}$ algorithm that trades off \textit{exploration v. exploitation} in the right way, and achieves expected regret that grows at most as near-$O(\log^2 T)$. The motivation comes from opportunistic spectrum access by multiple secondary users in cognitive radio networks wherein they must pick among various wireless channels that look different to different users. This is the first distributed learning algorithm for multi-player MABs to the best of our knowledge.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge