Deep Learning Framework for History Matching CO2 Storage with 4D Seismic and Monitoring Well Data

Geological carbon storage entails the injection of megatonnes of supercritical CO2 into subsurface formations. The properties of these formations are usually highly uncertain, which makes design and optimization of large-scale storage operations challenging. In this paper we introduce a history matching strategy that enables the calibration of formation properties based on early-time observations. Early-time assessments are essential to assure the operation is performing as planned. Our framework involves two fit-for-purpose deep learning surrogate models that provide predictions for in-situ monitoring well data and interpreted time-lapse (4D) seismic saturation data. These two types of data are at very different scales of resolution, so it is appropriate to construct separate, specialized deep learning networks for their prediction. This approach results in a workflow that is more straightforward to design and more efficient to train than a single surrogate that provides global high-fidelity predictions. The deep learning models are integrated into a hierarchical Markov chain Monte Carlo (MCMC) history matching procedure. History matching is performed on a synthetic case with and without 4D seismic data, which allows us to quantify the impact of 4D seismic on uncertainty reduction. The use of both data types is shown to provide substantial uncertainty reduction in key geomodel parameters and to enable accurate predictions of CO2 plume dynamics. The overall history matching framework developed in this study represents an efficient way to integrate multiple data types and to assess the impact of each on uncertainty reduction and performance predictions.

Deep learning based closed-loop optimization of geothermal reservoir production

To maximize the economic benefits of geothermal energy production, it is essential to optimize geothermal reservoir management strategies, in which geologic uncertainty should be considered. In this work, we propose a closed-loop optimization framework, based on deep learning surrogates, for the well control optimization of geothermal reservoirs. In this framework, we construct a hybrid convolution-recurrent neural network surrogate, which combines the convolution neural network (CNN) and long short-term memory (LSTM) recurrent network. The convolution structure can extract spatial information of geologic parameter fields and the recurrent structure can approximate sequence-to-sequence mapping. The trained model can predict time-varying production responses (rate, temperature, etc.) for cases with different permeability fields and well control sequences. In the closed-loop optimization framework, production optimization based on the differential evolution (DE) algorithm, and data assimilation based on the iterative ensemble smoother (IES), are performed alternately to achieve real-time well control optimization and geologic parameter estimation as the production proceeds. In addition, the averaged objective function over the ensemble of geologic parameter estimations is adopted to consider geologic uncertainty in the optimization process. Several geothermal reservoir development cases are designed to test the performance of the proposed production optimization framework. The results show that the proposed framework can achieve efficient and effective real-time optimization and data assimilation in the geothermal reservoir production process.

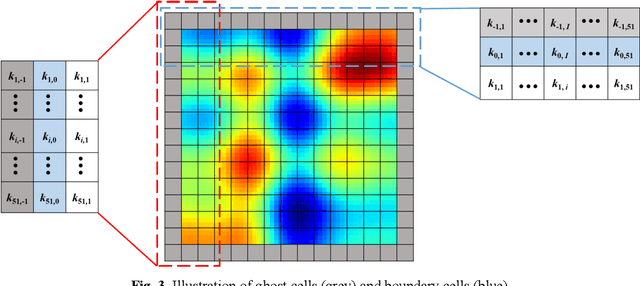
Deep-learning-based upscaling method for geologic models via theory-guided convolutional neural network

Large-scale or high-resolution geologic models usually comprise a huge number of grid blocks, which can be computationally demanding and time-consuming to solve with numerical simulators. Therefore, it is advantageous to upscale geologic models (e.g., hydraulic conductivity) from fine-scale (high-resolution grids) to coarse-scale systems. Numerical upscaling methods have been proven to be effective and robust for coarsening geologic models, but their efficiency remains to be improved. In this work, a deep-learning-based method is proposed to upscale the fine-scale geologic models, which can assist to improve upscaling efficiency significantly. In the deep learning method, a deep convolutional neural network (CNN) is trained to approximate the relationship between the coarse grid of hydraulic conductivity fields and the hydraulic heads, which can then be utilized to replace the numerical solvers while solving the flow equations for each coarse block. In addition, physical laws (e.g., governing equations and periodic boundary conditions) can also be incorporated into the training process of the deep CNN model, which is termed the theory-guided convolutional neural network (TgCNN). With the physical information considered, dependence on the data volume of training the deep learning models can be reduced greatly. Several subsurface flow cases are introduced to test the performance of the proposed deep-learning-based upscaling method, including 2D and 3D cases, and isotropic and anisotropic cases. The results show that the deep learning method can provide equivalent upscaling accuracy to the numerical method, and efficiency can be improved significantly compared to numerical upscaling.

Uncertainty quantification and inverse modeling for subsurface flow in 3D heterogeneous formations using a theory-guided convolutional encoder-decoder network

We build surrogate models for dynamic 3D subsurface single-phase flow problems with multiple vertical producing wells. The surrogate model provides efficient pressure estimation of the entire formation at any timestep given a stochastic permeability field, arbitrary well locations and penetration lengths, and a timestep matrix as inputs. The well production rate or bottom hole pressure can then be determined based on Peaceman's formula. The original surrogate modeling task is transformed into an image-to-image regression problem using a convolutional encoder-decoder neural network architecture. The residual of the governing flow equation in its discretized form is incorporated into the loss function to impose theoretical guidance on the model training process. As a result, the accuracy and generalization ability of the trained surrogate models are significantly improved compared to fully data-driven models. They are also shown to have flexible extrapolation ability to permeability fields with different statistics. The surrogate models are used to conduct uncertainty quantification considering a stochastic permeability field, as well as to infer unknown permeability information based on limited well production data and observation data of formation properties. Results are shown to be in good agreement with traditional numerical simulation tools, but computational efficiency is dramatically improved.

Surrogate and inverse modeling for two-phase flow in porous media via theory-guided convolutional neural network

The theory-guided convolutional neural network (TgCNN) framework, which can incorporate discretized governing equation residuals into the training of convolutional neural networks (CNNs), is extended to two-phase porous media flow problems in this work. The two principal variables of the considered problem, pressure and saturation, are approximated simultaneously with two CNNs, respectively. Pressure and saturation are coupled with each other in the governing equations, and thus the two networks are also mutually conditioned in the training process by the discretized governing equations, which also increases the difficulty of model training. The coupled and discretized equations can provide valuable information in the training process. With the assistance of theory-guidance, the TgCNN surrogates can achieve better accuracy than ordinary CNN surrogates in two-phase flow problems. Moreover, a piecewise training strategy is proposed for the scenario with varying well controls, in which the TgCNN surrogates are constructed for different segments on the time dimension and stacked together to predict solutions for the whole time-span. For scenarios with larger variance of the formation property field, the TgCNN surrogates can also achieve satisfactory performance. The constructed TgCNN surrogates are further used for inversion of permeability fields by combining them with the iterative ensemble smoother (IES) algorithm, and sufficient inversion accuracy is obtained with improved efficiency.

Theory-guided hard constraint projection (HCP): a knowledge-based data-driven scientific machine learning method

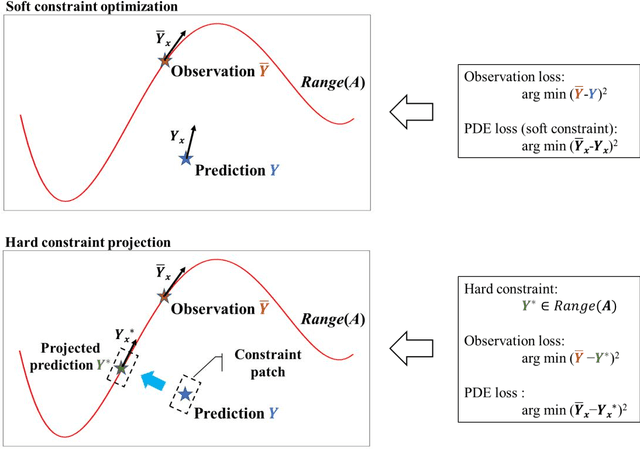
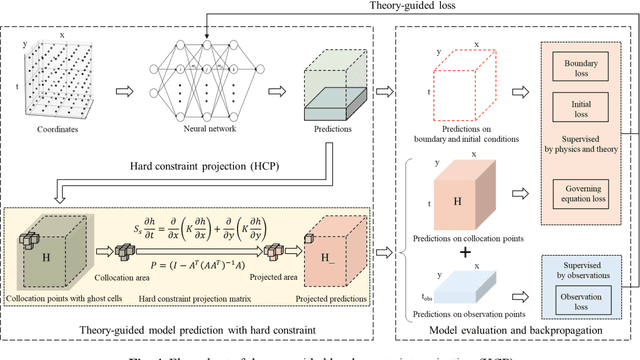
Machine learning models have been successfully used in many scientific and engineering fields. However, it remains difficult for a model to simultaneously utilize domain knowledge and experimental observation data. The application of knowledge-based symbolic AI represented by an expert system is limited by the expressive ability of the model, and data-driven connectionism AI represented by neural networks is prone to produce predictions that violate physical mechanisms. In order to fully integrate domain knowledge with observations, and make full use of the prior information and the strong fitting ability of neural networks, this study proposes theory-guided hard constraint projection (HCP). This model converts physical constraints, such as governing equations, into a form that is easy to handle through discretization, and then implements hard constraint optimization through projection. Based on rigorous mathematical proofs, theory-guided HCP can ensure that model predictions strictly conform to physical mechanisms in the constraint patch. The performance of the theory-guided HCP is verified by experiments based on the heterogeneous subsurface flow problem. Due to the application of hard constraints, compared with fully connected neural networks and soft constraint models, such as theory-guided neural networks and physics-informed neural networks, theory-guided HCP requires fewer data, and achieves higher prediction accuracy and stronger robustness to noisy observations.

Deep-learning based discovery of partial differential equations in integral form from sparse and noisy data

Data-driven discovery of partial differential equations (PDEs) has attracted increasing attention in recent years. Although significant progress has been made, certain unresolved issues remain. For example, for PDEs with high-order derivatives, the performance of existing methods is unsatisfactory, especially when the data are sparse and noisy. It is also difficult to discover heterogeneous parametric PDEs where heterogeneous parameters are embedded in the partial differential operators. In this work, a new framework combining deep-learning and integral form is proposed to handle the above-mentioned problems simultaneously, and improve the accuracy and stability of PDE discovery. In the framework, a deep neural network is firstly trained with observation data to generate meta-data and calculate derivatives. Then, a unified integral form is defined, and the genetic algorithm is employed to discover the best structure. Finally, the value of parameters is calculated, and whether the parameters are constants or variables is identified. Numerical experiments proved that our proposed algorithm is more robust to noise and more accurate compared with existing methods due to the utilization of integral form. Our proposed algorithm is also able to discover PDEs with high-order derivatives or heterogeneous parameters accurately with sparse and noisy data.

Theory-guided Auto-Encoder for Surrogate Construction and Inverse Modeling

A Theory-guided Auto-Encoder (TgAE) framework is proposed for surrogate construction and is further used for uncertainty quantification and inverse modeling tasks. The framework is built based on the Auto-Encoder (or Encoder-Decoder) architecture of convolutional neural network (CNN) via a theory-guided training process. In order to achieve the theory-guided training, the governing equations of the studied problems can be discretized and the finite difference scheme of the equations can be embedded into the training of CNN. The residual of the discretized governing equations as well as the data mismatch constitute the loss function of the TgAE. The trained TgAE can be used to construct a surrogate that approximates the relationship between the model parameters and responses with limited labeled data. In order to test the performance of the TgAE, several subsurface flow cases are introduced. The results show the satisfactory accuracy of the TgAE surrogate and efficiency of uncertainty quantification tasks can be improved with the TgAE surrogate. The TgAE also shows good extrapolation ability for cases with different correlation lengths and variances. Furthermore, the parameter inversion task has been implemented with the TgAE surrogate and satisfactory results can be obtained.

Weak Form Theory-guided Neural Network for Deep Learning of Subsurface Single and Two-phase Flow

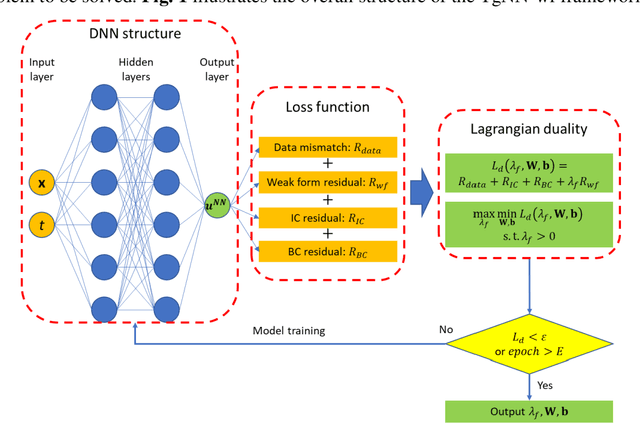
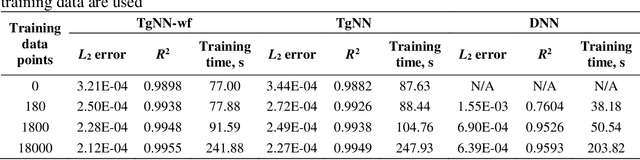
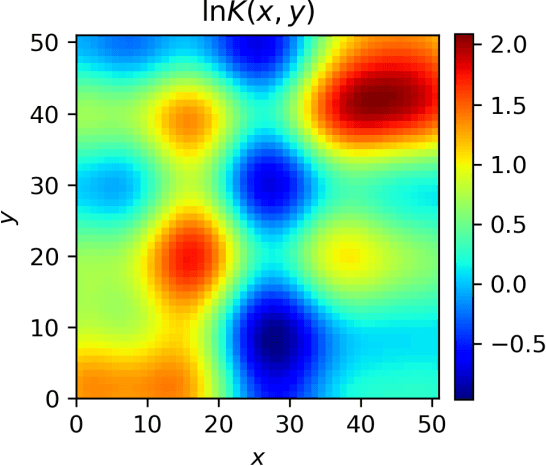
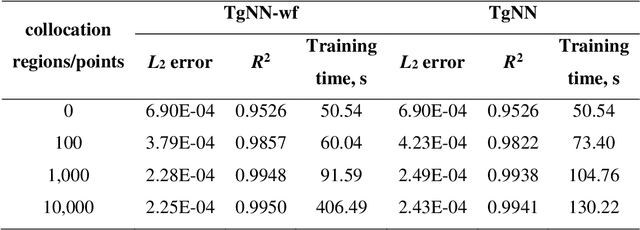
Deep neural networks (DNNs) are widely used as surrogate models in geophysical applications; incorporating theoretical guidance into DNNs has improved the generalizability. However, most of such approaches define the loss function based on the strong form of conservation laws (via partial differential equations, PDEs), which is subject to deteriorated accuracy when the PDE has high order derivatives or the solution has strong discontinuities. Herein, we propose a weak form theory-guided neural network (TgNN-wf), which incorporates the weak form formulation of the PDE into the loss function combined with data constraint and initial and boundary conditions regularizations to tackle the aforementioned difficulties. In the weak form, high order derivatives in the PDE can be transferred to the test functions by performing integration-by-parts, which reduces computational error. We use domain decomposition with locally defined test functions, which captures local discontinuity effectively. Two numerical cases demonstrate the superiority of the proposed TgNN-wf over the strong form TgNN, including the hydraulic head prediction for unsteady-state 2D single-phase flow problems and the saturation profile prediction for 1D two-phase flow problems. Results show that TgNN-wf consistently has higher accuracy than TgNN, especially when strong discontinuity in the solution is present. TgNN-wf also trains faster than TgNN when the number of integration subdomains is not too large (<10,000). Moreover, TgNN-wf is more robust to noises. Thus, the proposed TgNN-wf paves the way for which a variety of deep learning problems in the small data regime can be solved more accurately and efficiently.

A Lagrangian Dual-based Theory-guided Deep Neural Network

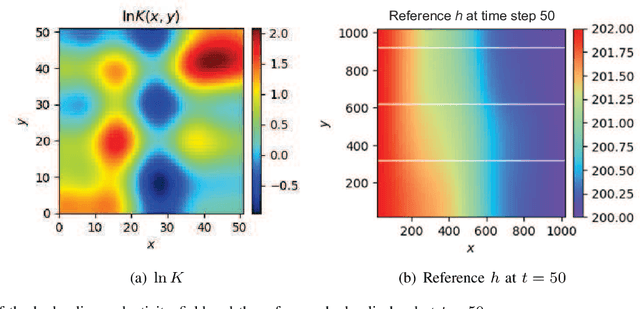
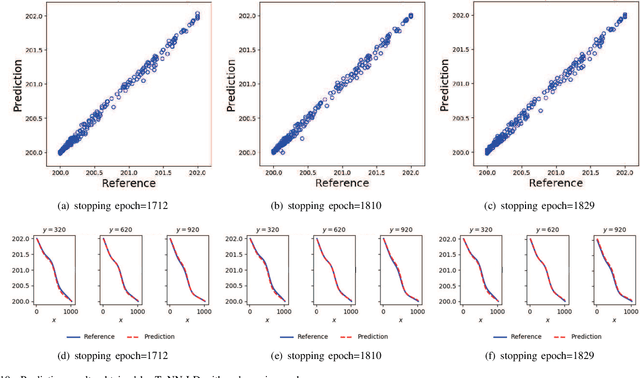
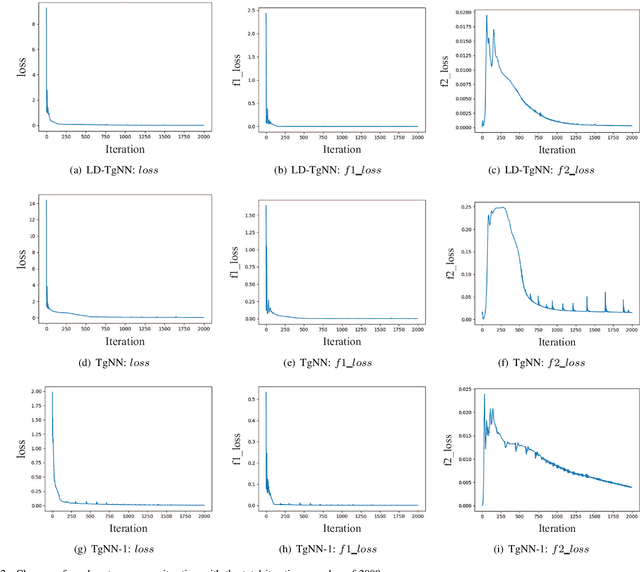
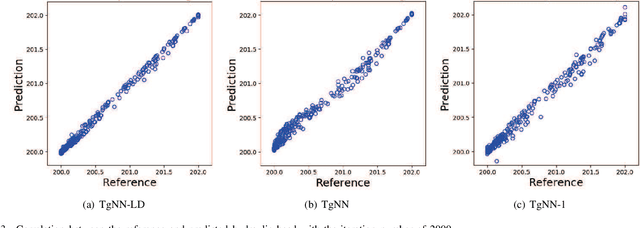
The theory-guided neural network (TgNN) is a kind of method which improves the effectiveness and efficiency of neural network architectures by incorporating scientific knowledge or physical information. Despite its great success, the theory-guided (deep) neural network possesses certain limits when maintaining a tradeoff between training data and domain knowledge during the training process. In this paper, the Lagrangian dual-based TgNN (TgNN-LD) is proposed to improve the effectiveness of TgNN. We convert the original loss function into a constrained form with fewer items, in which partial differential equations (PDEs), engineering controls (ECs), and expert knowledge (EK) are regarded as constraints, with one Lagrangian variable per constraint. These Lagrangian variables are incorporated to achieve an equitable tradeoff between observation data and corresponding constraints, in order to improve prediction accuracy, and conserve time and computational resources adjusted by an ad-hoc procedure. To investigate the performance of the proposed method, the original TgNN model with a set of optimized weight values adjusted by ad-hoc procedures is compared on a subsurface flow problem, with their L2 error, R square (R2), and computational time being analyzed. Experimental results demonstrate the superiority of the Lagrangian dual-based TgNN.