Discovery of partial differential equations from highly noisy and sparse data with physics-informed information criterion

Data-driven discovery of PDEs has made tremendous progress recently, and many canonical PDEs have been discovered successfully for proof-of-concept. However, determining the most proper PDE without prior references remains challenging in terms of practical applications. In this work, a physics-informed information criterion (PIC) is proposed to measure the parsimony and precision of the discovered PDE synthetically. The proposed PIC achieves state-of-the-art robustness to highly noisy and sparse data on seven canonical PDEs from different physical scenes, which confirms its ability to handle difficult situations. The PIC is also employed to discover unrevealed macroscale governing equations from microscopic simulation data in an actual physical scene. The results show that the discovered macroscale PDE is precise and parsimonious, and satisfies underlying symmetries, which facilitates understanding and simulation of the physical process. The proposition of PIC enables practical applications of PDE discovery in discovering unrevealed governing equations in broader physical scenes.

Constructing Sub-scale Surrogate Model for Proppant Settling in Inclined Fractures from Simulation Data with Multi-fidelity Neural Network

Particle settling in inclined channels is an important phenomenon that occurs during hydraulic fracturing of shale gas production. Generally, in order to accurately simulate the large-scale (field-scale) proppant transport process, constructing a fast and accurate sub-scale proppant settling model, or surrogate model, becomes a critical issue, since mapping between physical parameters and proppant settling velocity is complex. Previously, particle settling has usually been investigated via high-fidelity experiments and meso-scale numerical simulations, both of which are time-consuming. In this work, a new method is proposed and utilized, i.e., the multi-fidelity neural network (MFNN), to construct a settling surrogate model, which could utilize both high-fidelity and low-fidelity (thus, less expensive) data. The results demonstrate that constructing the settling surrogate with the MFNN can reduce the need for high-fidelity data and thus computational cost by 80%, while the accuracy lost is less than 5% compared to a high-fidelity surrogate. Moreover, the investigated particle settling surrogate is applied in macro-scale proppant transport simulation, which shows that the settling model is significant to proppant transport and yields accurate results. This opens novel pathways for rapidly predicting proppant settling velocity in reservoir applications.

Deep-Learning Discovers Macroscopic Governing Equations for Viscous Gravity Currents from Microscopic Simulation Data

Although deep-learning has been successfully applied in a variety of science and engineering problems owing to its strong high-dimensional nonlinear mapping capability, it is of limited use in scientific knowledge discovery. In this work, we propose a deep-learning based framework to discover the macroscopic governing equation of viscous gravity current based on high-resolution microscopic simulation data without the need for prior knowledge of underlying terms. For two typical scenarios with different viscosity ratios, the deep-learning based equations exactly capture the same dominated terms as the theoretically derived equations for describing long-term asymptotic behaviors, which validates the proposed framework. Unknown macroscopic equations are then obtained for describing short-term behaviors, and hidden mechanisms are eventually discovered with deep-learned explainable compensation terms and corresponding coefficients. Consequently, the presented deep-learning framework shows considerable potential for discovering unrevealed intrinsic laws in scientific semantic space from raw experimental or simulation results in data space.

Theory-guided hard constraint projection (HCP): a knowledge-based data-driven scientific machine learning method

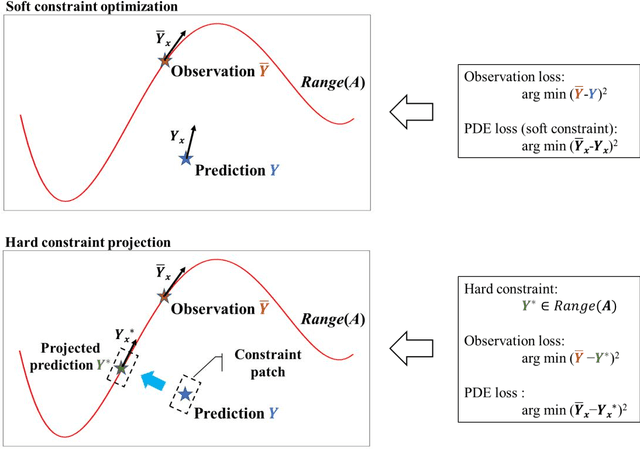
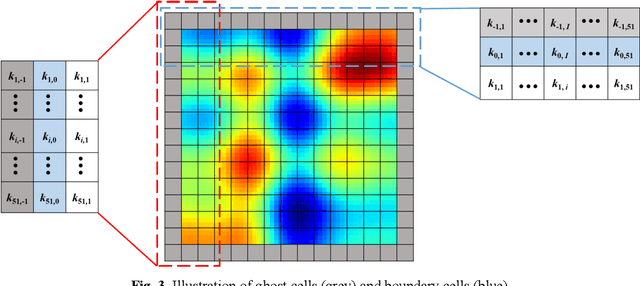
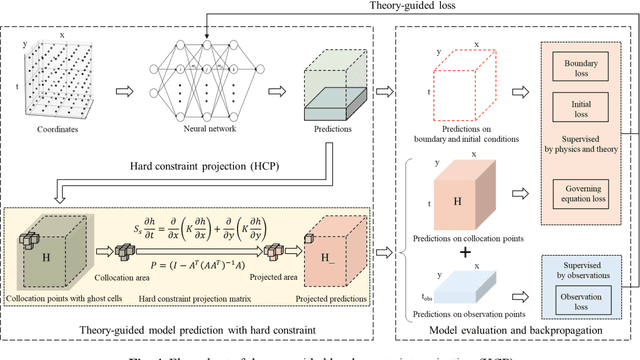
Machine learning models have been successfully used in many scientific and engineering fields. However, it remains difficult for a model to simultaneously utilize domain knowledge and experimental observation data. The application of knowledge-based symbolic AI represented by an expert system is limited by the expressive ability of the model, and data-driven connectionism AI represented by neural networks is prone to produce predictions that violate physical mechanisms. In order to fully integrate domain knowledge with observations, and make full use of the prior information and the strong fitting ability of neural networks, this study proposes theory-guided hard constraint projection (HCP). This model converts physical constraints, such as governing equations, into a form that is easy to handle through discretization, and then implements hard constraint optimization through projection. Based on rigorous mathematical proofs, theory-guided HCP can ensure that model predictions strictly conform to physical mechanisms in the constraint patch. The performance of the theory-guided HCP is verified by experiments based on the heterogeneous subsurface flow problem. Due to the application of hard constraints, compared with fully connected neural networks and soft constraint models, such as theory-guided neural networks and physics-informed neural networks, theory-guided HCP requires fewer data, and achieves higher prediction accuracy and stronger robustness to noisy observations.

Deep-learning of Parametric Partial Differential Equations from Sparse and Noisy Data

Data-driven methods have recently made great progress in the discovery of partial differential equations (PDEs) from spatial-temporal data. However, several challenges remain to be solved, including sparse noisy data, incomplete candidate library, and spatially- or temporally-varying coefficients. In this work, a new framework, which combines neural network, genetic algorithm and adaptive methods, is put forward to address all of these challenges simultaneously. In the framework, a trained neural network is utilized to calculate derivatives and generate a large amount of meta-data, which solves the problem of sparse noisy data. Next, genetic algorithm is utilized to discover the form of PDEs and corresponding coefficients with an incomplete candidate library. Finally, a two-step adaptive method is introduced to discover parametric PDEs with spatially- or temporally-varying coefficients. In this method, the structure of a parametric PDE is first discovered, and then the general form of varying coefficients is identified. The proposed algorithm is tested on the Burgers equation, the convection-diffusion equation, the wave equation, and the KdV equation. The results demonstrate that this method is robust to sparse and noisy data, and is able to discover parametric PDEs with an incomplete candidate library.