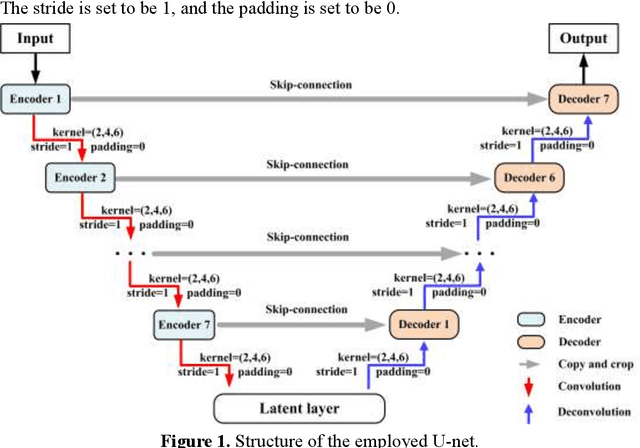
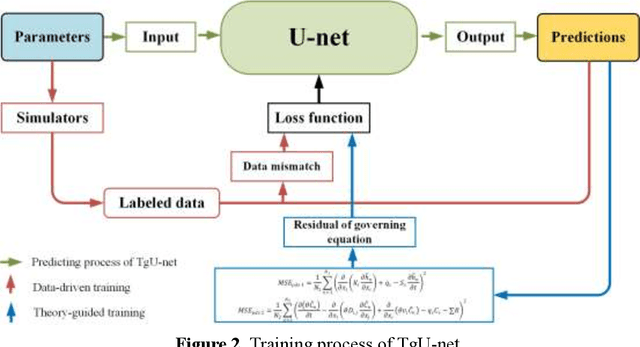
Identification of Physical Processes and Unknown Parameters of 3D Groundwater Contaminant Problems via Theory-guided U-net

Identification of unknown physical processes and parameters of groundwater contaminant sources is a challenging task due to their ill-posed and non-unique nature. Numerous works have focused on determining nonlinear physical processes through model selection methods. However, identifying corresponding nonlinear systems for different physical phenomena using numerical methods can be computationally prohibitive. With the advent of machine learning (ML) algorithms, more efficient surrogate models based on neural networks (NNs) have been developed in various disciplines. In this work, a theory-guided U-net (TgU-net) framework is proposed for surrogate modeling of three-dimensional (3D) groundwater contaminant problems in order to efficiently elucidate their involved processes and unknown parameters. In TgU-net, the underlying governing equations are embedded into the loss function of U-net as soft constraints. For the considered groundwater contaminant problem, sorption is considered to be a potential process of an uncertain type, and three equilibrium sorption isotherm types (i.e., linear, Freundlich, and Langmuir) are considered. Different from traditional approaches in which one model corresponds to one equation, these three sorption types are modeled through only one TgU-net surrogate. The three mentioned sorption terms are integrated into one equation by assigning indicators. Accurate predictions illustrate the satisfactory generalizability and extrapolability of the constructed TgU-net. Furthermore, based on the constructed TgU-net surrogate, a data assimilation method is employed to identify the physical process and parameters simultaneously. This work shows the possibility of governing equation discovery of physical problems that contain multiple and even uncertain processes by using deep learning and data assimilation methods.

Deep learning based closed-loop optimization of geothermal reservoir production

To maximize the economic benefits of geothermal energy production, it is essential to optimize geothermal reservoir management strategies, in which geologic uncertainty should be considered. In this work, we propose a closed-loop optimization framework, based on deep learning surrogates, for the well control optimization of geothermal reservoirs. In this framework, we construct a hybrid convolution-recurrent neural network surrogate, which combines the convolution neural network (CNN) and long short-term memory (LSTM) recurrent network. The convolution structure can extract spatial information of geologic parameter fields and the recurrent structure can approximate sequence-to-sequence mapping. The trained model can predict time-varying production responses (rate, temperature, etc.) for cases with different permeability fields and well control sequences. In the closed-loop optimization framework, production optimization based on the differential evolution (DE) algorithm, and data assimilation based on the iterative ensemble smoother (IES), are performed alternately to achieve real-time well control optimization and geologic parameter estimation as the production proceeds. In addition, the averaged objective function over the ensemble of geologic parameter estimations is adopted to consider geologic uncertainty in the optimization process. Several geothermal reservoir development cases are designed to test the performance of the proposed production optimization framework. The results show that the proposed framework can achieve efficient and effective real-time optimization and data assimilation in the geothermal reservoir production process.

Deep-learning-based upscaling method for geologic models via theory-guided convolutional neural network

Large-scale or high-resolution geologic models usually comprise a huge number of grid blocks, which can be computationally demanding and time-consuming to solve with numerical simulators. Therefore, it is advantageous to upscale geologic models (e.g., hydraulic conductivity) from fine-scale (high-resolution grids) to coarse-scale systems. Numerical upscaling methods have been proven to be effective and robust for coarsening geologic models, but their efficiency remains to be improved. In this work, a deep-learning-based method is proposed to upscale the fine-scale geologic models, which can assist to improve upscaling efficiency significantly. In the deep learning method, a deep convolutional neural network (CNN) is trained to approximate the relationship between the coarse grid of hydraulic conductivity fields and the hydraulic heads, which can then be utilized to replace the numerical solvers while solving the flow equations for each coarse block. In addition, physical laws (e.g., governing equations and periodic boundary conditions) can also be incorporated into the training process of the deep CNN model, which is termed the theory-guided convolutional neural network (TgCNN). With the physical information considered, dependence on the data volume of training the deep learning models can be reduced greatly. Several subsurface flow cases are introduced to test the performance of the proposed deep-learning-based upscaling method, including 2D and 3D cases, and isotropic and anisotropic cases. The results show that the deep learning method can provide equivalent upscaling accuracy to the numerical method, and efficiency can be improved significantly compared to numerical upscaling.

Surrogate and inverse modeling for two-phase flow in porous media via theory-guided convolutional neural network

The theory-guided convolutional neural network (TgCNN) framework, which can incorporate discretized governing equation residuals into the training of convolutional neural networks (CNNs), is extended to two-phase porous media flow problems in this work. The two principal variables of the considered problem, pressure and saturation, are approximated simultaneously with two CNNs, respectively. Pressure and saturation are coupled with each other in the governing equations, and thus the two networks are also mutually conditioned in the training process by the discretized governing equations, which also increases the difficulty of model training. The coupled and discretized equations can provide valuable information in the training process. With the assistance of theory-guidance, the TgCNN surrogates can achieve better accuracy than ordinary CNN surrogates in two-phase flow problems. Moreover, a piecewise training strategy is proposed for the scenario with varying well controls, in which the TgCNN surrogates are constructed for different segments on the time dimension and stacked together to predict solutions for the whole time-span. For scenarios with larger variance of the formation property field, the TgCNN surrogates can also achieve satisfactory performance. The constructed TgCNN surrogates are further used for inversion of permeability fields by combining them with the iterative ensemble smoother (IES) algorithm, and sufficient inversion accuracy is obtained with improved efficiency.

Theory-guided Auto-Encoder for Surrogate Construction and Inverse Modeling

A Theory-guided Auto-Encoder (TgAE) framework is proposed for surrogate construction and is further used for uncertainty quantification and inverse modeling tasks. The framework is built based on the Auto-Encoder (or Encoder-Decoder) architecture of convolutional neural network (CNN) via a theory-guided training process. In order to achieve the theory-guided training, the governing equations of the studied problems can be discretized and the finite difference scheme of the equations can be embedded into the training of CNN. The residual of the discretized governing equations as well as the data mismatch constitute the loss function of the TgAE. The trained TgAE can be used to construct a surrogate that approximates the relationship between the model parameters and responses with limited labeled data. In order to test the performance of the TgAE, several subsurface flow cases are introduced. The results show the satisfactory accuracy of the TgAE surrogate and efficiency of uncertainty quantification tasks can be improved with the TgAE surrogate. The TgAE also shows good extrapolation ability for cases with different correlation lengths and variances. Furthermore, the parameter inversion task has been implemented with the TgAE surrogate and satisfactory results can be obtained.

Efficient Uncertainty Quantification for Dynamic Subsurface Flow with Surrogate by Theory-guided Neural Network

Subsurface flow problems usually involve some degree of uncertainty. Consequently, uncertainty quantification is commonly necessary for subsurface flow prediction. In this work, we propose a methodology for efficient uncertainty quantification for dynamic subsurface flow with a surrogate constructed by the Theory-guided Neural Network (TgNN). The TgNN here is specially designed for problems with stochastic parameters. In the TgNN, stochastic parameters, time and location comprise the input of the neural network, while the quantity of interest is the output. The neural network is trained with available simulation data, while being simultaneously guided by theory (e.g., the governing equation, boundary conditions, initial conditions, etc.) of the underlying problem. The trained neural network can predict solutions of subsurface flow problems with new stochastic parameters. With the TgNN surrogate, the Monte Carlo (MC) method can be efficiently implemented for uncertainty quantification. The proposed methodology is evaluated with two-dimensional dynamic saturated flow problems in porous medium. Numerical results show that the TgNN based surrogate can significantly improve the efficiency of uncertainty quantification tasks compared with simulation based implementation. Further investigations regarding stochastic fields with smaller correlation length, larger variance, changing boundary values and out-of-distribution variances are performed, and satisfactory results are obtained.

DLGA-PDE: Discovery of PDEs with incomplete candidate library via combination of deep learning and genetic algorithm

Data-driven methods have recently been developed to discover underlying partial differential equations (PDEs) of physical problems. However, for these methods, a complete candidate library of potential terms in a PDE are usually required. To overcome this limitation, we propose a novel framework combining deep learning and genetic algorithm, called DLGA-PDE, for discovering PDEs. In the proposed framework, a deep neural network that is trained with available data of a physical problem is utilized to generate meta-data and calculate derivatives, and the genetic algorithm is then employed to discover the underlying PDE. Owing to the merits of the genetic algorithm, such as mutation and crossover, DLGA-PDE can work with an incomplete candidate library. The proposed DLGA-PDE is tested for discovery of the Korteweg-de Vries (KdV) equation, the Burgers equation, the wave equation, and the Chaffee-Infante equation, respectively, for proof-of-concept. Satisfactory results are obtained without the need for a complete candidate library, even in the presence of noisy and limited data.

Deep Learning of Subsurface Flow via Theory-guided Neural Network

Active researches are currently being performed to incorporate the wealth of scientific knowledge into data-driven approaches (e.g., neural networks) in order to improve the latter's effectiveness. In this study, the Theory-guided Neural Network (TgNN) is proposed for deep learning of subsurface flow. In the TgNN, as supervised learning, the neural network is trained with available observations or simulation data while being simultaneously guided by theory (e.g., governing equations, other physical constraints, engineering controls, and expert knowledge) of the underlying problem. The TgNN can achieve higher accuracy than the ordinary Artificial Neural Network (ANN) because the former provides physically feasible predictions and can be more readily generalized beyond the regimes covered with the training data. Furthermore, the TgNN model is proposed for subsurface flow with heterogeneous model parameters. Several numerical cases of two-dimensional transient saturated flow are introduced to test the performance of the TgNN. In the learning process, the loss function contains data mismatch, as well as PDE constraint, engineering control, and expert knowledge. After obtaining the parameters of the neural network by minimizing the loss function, a TgNN model is built that not only fits the data, but also adheres to physical/engineering constraints. Predicting the future response can be easily realized by the TgNN model. In addition, the TgNN model is tested in more complicated scenarios, such as prediction with changed boundary conditions, learning from noisy data or outliers, transfer learning, and engineering controls. Numerical results demonstrate that the TgNN model achieves much better predictability, reliability, and generalizability than ANN models due to the physical/engineering constraints in the former.

DL-PDE: Deep-learning based data-driven discovery of partial differential equations from discrete and noisy data

In recent years, data-driven methods have been utilized to learn dynamical systems and partial differential equations (PDE). However, major challenges remain to be resolved, including learning PDE under noisy data and limited discrete data. To overcome these challenges, in this work, a deep-learning based data-driven method, called DL-PDE, is developed to discover the governing PDEs of underlying physical processes. The DL-PDE method combines deep learning via neural networks and data-driven discovery of PDEs via sparse regressions, such as the least absolute shrinkage and selection operator (Lasso) and sequential threshold ridge regression (STRidge). In this method, derivatives are calculated by automatic differentiation from the deep neural network, and equation form and coefficients are obtained with sparse regressions. The DL-PDE is tested with physical processes, governed by groundwater flow equation, contaminant transport equation, Burgers equation and Korteweg-de Vries (KdV) equation, for proof-of-concept and applications in real-world engineering settings. The proposed DL-PDE achieves satisfactory results when data are discrete and noisy.

Identification of physical processes via combined data-driven and data-assimilation methods

With the advent of modern data collection and storage technologies, data-driven approaches have been developed for discovering the governing partial differential equations (PDE) of physical problems. However, in the extant works the model parameters in the equations are either assumed to be known or have a linear dependency. Therefore, most of the realistic physical processes cannot be identified with the current data-driven PDE discovery approaches. In this study, an innovative framework is developed that combines data-driven and data-assimilation methods for simultaneously identifying physical processes and inferring model parameters. Spatiotemporal measurement data are first divided into a training data set and a testing data set. Using the training data set, a data-driven method is developed to learn the governing equation of the considered physical problem by identifying the occurred (or dominated) processes and selecting the proper empirical model. Through introducing a prediction error of the learned governing equation for the testing data set, a data-assimilation method is devised to estimate the uncertain model parameters of the selected empirical model. For the contaminant transport problem investigated, the results demonstrate that the proposed method can adequately identify the considered physical processes via concurrently discovering the corresponding governing equations and inferring uncertain parameters of nonlinear models, even in the presence of measurement errors. This work helps to broaden the applicable area of the research of data driven discovery of governing equations of physical problems.