Factory Operators' Perspectives on Cognitive Assistants for Knowledge Sharing: Challenges, Risks, and Impact on Work

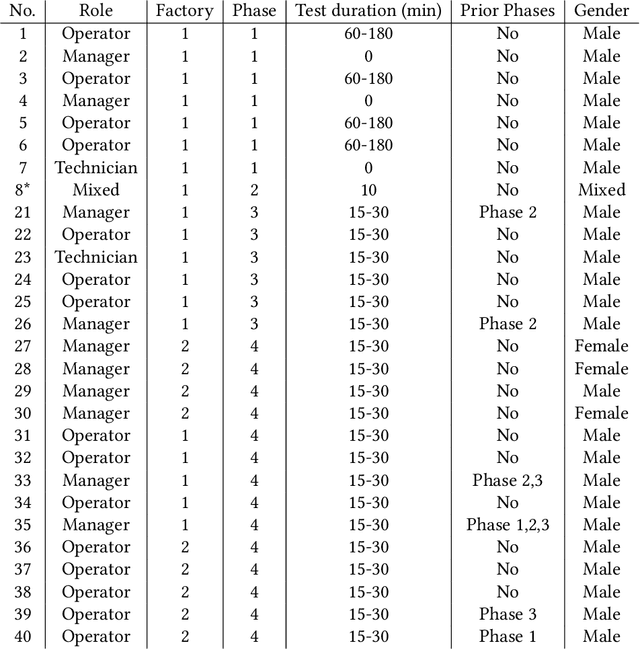
In the shift towards human-centered manufacturing, our two-year longitudinal study investigates the real-world impact of deploying Cognitive Assistants (CAs) in factories. The CAs were designed to facilitate knowledge sharing among factory operators. Our investigation focused on smartphone-based voice assistants and LLM-powered chatbots, examining their usability and utility in a real-world factory setting. Based on the qualitative feedback we collected during the deployments of CAs at the factories, we conducted a thematic analysis to investigate the perceptions, challenges, and overall impact on workflow and knowledge sharing. Our results indicate that while CAs have the potential to significantly improve efficiency through knowledge sharing and quicker resolution of production issues, they also introduce concerns around workplace surveillance, the types of knowledge that can be shared, and shortcomings compared to human-to-human knowledge sharing. Additionally, our findings stress the importance of addressing privacy, knowledge contribution burdens, and tensions between factory operators and their managers.

Uncertainty quantification of two-phase flow in porous media via coupled-TgNN surrogate model

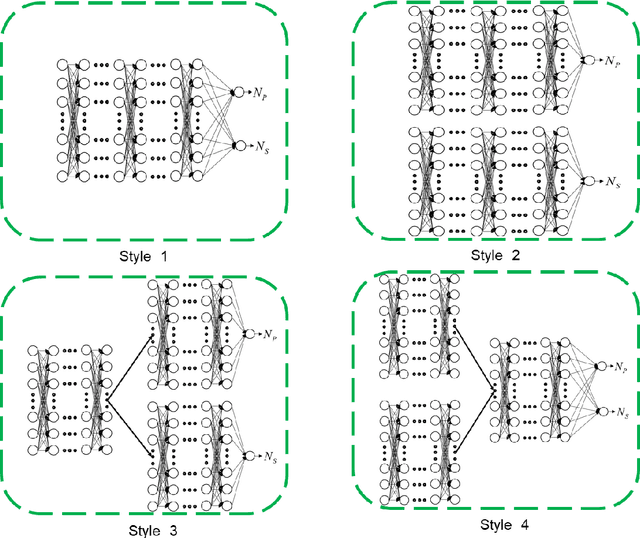
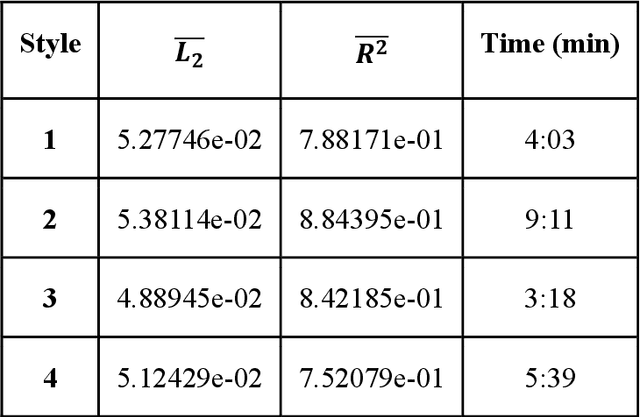
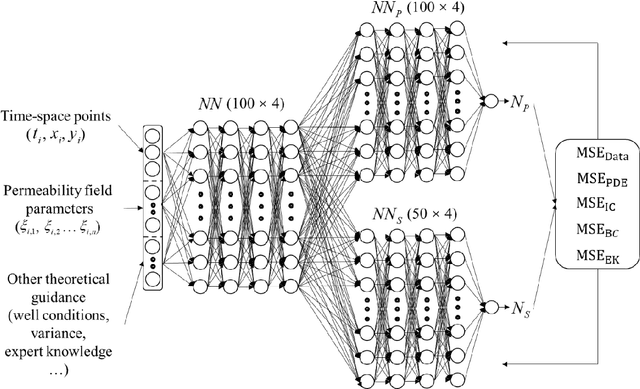
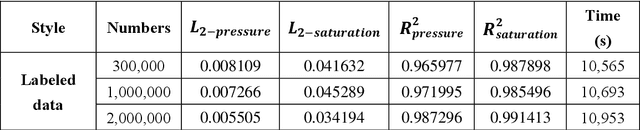
Uncertainty quantification (UQ) of subsurface two-phase flow usually requires numerous executions of forward simulations under varying conditions. In this work, a novel coupled theory-guided neural network (TgNN) based surrogate model is built to facilitate computation efficiency under the premise of satisfactory accuracy. The core notion of this proposed method is to bridge two separate blocks on top of an overall network. They underlie the TgNN model in a coupled form, which reflects the coupling nature of pressure and water saturation in the two-phase flow equation. The TgNN model not only relies on labeled data, but also incorporates underlying scientific theory and experiential rules (e.g., governing equations, stochastic parameter fields, boundary and initial conditions, well conditions, and expert knowledge) as additional components into the loss function. The performance of the TgNN-based surrogate model for two-phase flow problems is tested by different numbers of labeled data and collocation points, as well as the existence of data noise. The proposed TgNN-based surrogate model offers an effective way to solve the coupled nonlinear two-phase flow problem and demonstrates good accuracy and strong robustness when compared with the purely data-driven surrogate model. By combining the accurate TgNN-based surrogate model with the Monte Carlo method, UQ tasks can be performed at a minimum cost to evaluate statistical quantities. Since the heterogeneity of the random fields strongly impacts the results of the surrogate model, corresponding variance and correlation length are added to the input of the neural network to maintain its predictive capacity. The results show that the TgNN-based surrogate model achieves satisfactory accuracy, stability, and efficiency in UQ problems of subsurface two-phase flow.

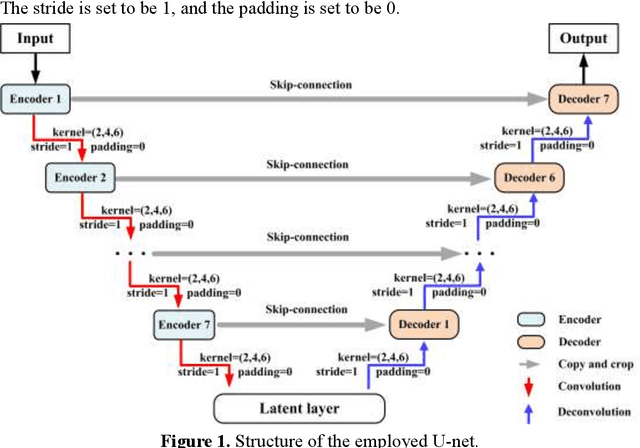
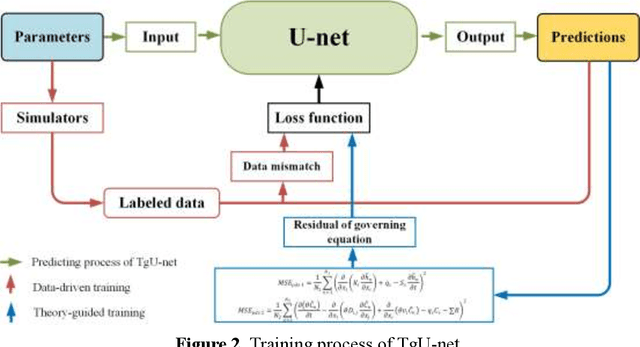
Identification of Physical Processes and Unknown Parameters of 3D Groundwater Contaminant Problems via Theory-guided U-net

Identification of unknown physical processes and parameters of groundwater contaminant sources is a challenging task due to their ill-posed and non-unique nature. Numerous works have focused on determining nonlinear physical processes through model selection methods. However, identifying corresponding nonlinear systems for different physical phenomena using numerical methods can be computationally prohibitive. With the advent of machine learning (ML) algorithms, more efficient surrogate models based on neural networks (NNs) have been developed in various disciplines. In this work, a theory-guided U-net (TgU-net) framework is proposed for surrogate modeling of three-dimensional (3D) groundwater contaminant problems in order to efficiently elucidate their involved processes and unknown parameters. In TgU-net, the underlying governing equations are embedded into the loss function of U-net as soft constraints. For the considered groundwater contaminant problem, sorption is considered to be a potential process of an uncertain type, and three equilibrium sorption isotherm types (i.e., linear, Freundlich, and Langmuir) are considered. Different from traditional approaches in which one model corresponds to one equation, these three sorption types are modeled through only one TgU-net surrogate. The three mentioned sorption terms are integrated into one equation by assigning indicators. Accurate predictions illustrate the satisfactory generalizability and extrapolability of the constructed TgU-net. Furthermore, based on the constructed TgU-net surrogate, a data assimilation method is employed to identify the physical process and parameters simultaneously. This work shows the possibility of governing equation discovery of physical problems that contain multiple and even uncertain processes by using deep learning and data assimilation methods.

Deep Learning of Dynamic Subsurface Flow via Theory-guided Generative Adversarial Network

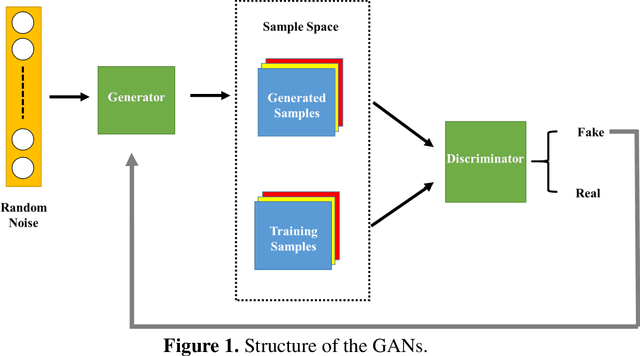
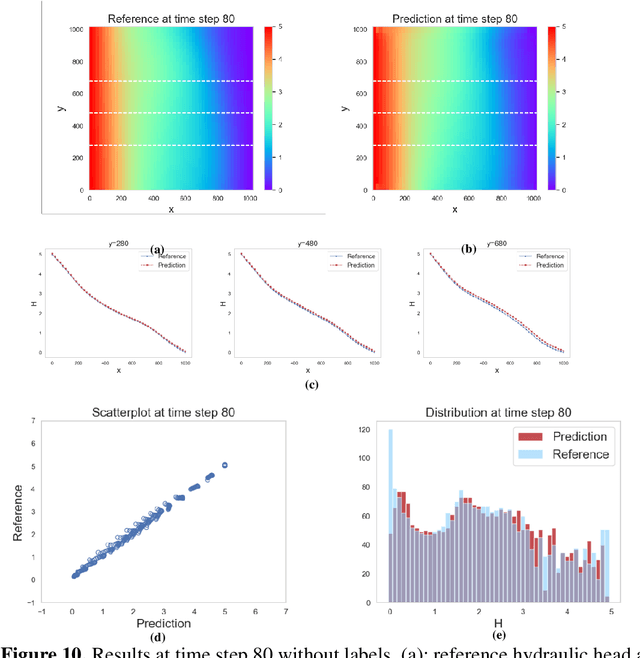
Generative adversarial network (GAN) has been shown to be useful in various applications, such as image recognition, text processing and scientific computing, due its strong ability to learn complex data distributions. In this study, a theory-guided generative adversarial network (TgGAN) is proposed to solve dynamic partial differential equations (PDEs). Different from standard GANs, the training term is no longer the true data and the generated data, but rather their residuals. In addition, such theories as governing equations, other physical constraints and engineering controls, are encoded into the loss function of the generator to ensure that the prediction does not only honor the training data, but also obey these theories. TgGAN is proposed for dynamic subsurface flow with heterogeneous model parameters, and the data at each time step are treated as a two-dimensional image. In this study, several numerical cases are introduced to test the performance of the TgGAN. Predicting the future response, label-free learning and learning from noisy data can be realized easily by the TgGAN model. The effects of the number of training data and the collocation points are also discussed. In order to improve the efficiency of TgGAN, the transfer learning algorithm is also employed. Numerical results demonstrate that the TgGAN model is robust and reliable for deep learning of dynamic PDEs.