PMT-MAE: Dual-Branch Self-Supervised Learning with Distillation for Efficient Point Cloud Classification

Advances in self-supervised learning are essential for enhancing feature extraction and understanding in point cloud processing. This paper introduces PMT-MAE (Point MLP-Transformer Masked Autoencoder), a novel self-supervised learning framework for point cloud classification. PMT-MAE features a dual-branch architecture that integrates Transformer and MLP components to capture rich features. The Transformer branch leverages global self-attention for intricate feature interactions, while the parallel MLP branch processes tokens through shared fully connected layers, offering a complementary feature transformation pathway. A fusion mechanism then combines these features, enhancing the model's capacity to learn comprehensive 3D representations. Guided by the sophisticated teacher model Point-M2AE, PMT-MAE employs a distillation strategy that includes feature distillation during pre-training and logit distillation during fine-tuning, ensuring effective knowledge transfer. On the ModelNet40 classification task, achieving an accuracy of 93.6\% without employing voting strategy, PMT-MAE surpasses the baseline Point-MAE (93.2\%) and the teacher Point-M2AE (93.4\%), underscoring its ability to learn discriminative 3D point cloud representations. Additionally, this framework demonstrates high efficiency, requiring only 40 epochs for both pre-training and fine-tuning. PMT-MAE's effectiveness and efficiency render it well-suited for scenarios with limited computational resources, positioning it as a promising solution for practical point cloud analysis.

Efficient Point Cloud Classification via Offline Distillation Framework and Negative-Weight Self-Distillation Technique

The rapid advancement in point cloud processing technologies has significantly increased the demand for efficient and compact models that achieve high-accuracy classification. Knowledge distillation has emerged as a potent model compression technique. However, traditional KD often requires extensive computational resources for forward inference of large teacher models, thereby reducing training efficiency for student models and increasing resource demands. To address these challenges, we introduce an innovative offline recording strategy that avoids the simultaneous loading of both teacher and student models, thereby reducing hardware demands. This approach feeds a multitude of augmented samples into the teacher model, recording both the data augmentation parameters and the corresponding logit outputs. By applying shape-level augmentation operations such as random scaling and translation, while excluding point-level operations like random jittering, the size of the records is significantly reduced. Additionally, to mitigate the issue of small student model over-imitating the teacher model's outputs and converging to suboptimal solutions, we incorporate a negative-weight self-distillation strategy. Experimental results demonstrate that the proposed distillation strategy enables the student model to achieve performance comparable to state-of-the-art models while maintaining lower parameter count. This approach strikes an optimal balance between performance and complexity. This study highlights the potential of our method to optimize knowledge distillation for point cloud classification tasks, particularly in resource-constrained environments, providing a novel solution for efficient point cloud analysis.

SA-MLP: Enhancing Point Cloud Classification with Efficient Addition and Shift Operations in MLP Architectures

This study addresses the computational inefficiencies in point cloud classification by introducing novel MLP-based architectures inspired by recent advances in CNN optimization. Traditional neural networks heavily rely on multiplication operations, which are computationally expensive. To tackle this, we propose Add-MLP and Shift-MLP, which replace multiplications with addition and shift operations, respectively, significantly enhancing computational efficiency. Building on this, we introduce SA-MLP, a hybrid model that intermixes alternately distributed shift and adder layers to replace MLP layers, maintaining the original number of layers without freezing shift layer weights. This design contrasts with the ShiftAddNet model from previous literature, which replaces convolutional layers with shift and adder layers, leading to a doubling of the number of layers and limited representational capacity due to frozen shift weights. Moreover, SA-MLP optimizes learning by setting distinct learning rates and optimizers specifically for the adder and shift layers, fully leveraging their complementary strengths. Extensive experiments demonstrate that while Add-MLP and Shift-MLP achieve competitive performance, SA-MLP significantly surpasses the multiplication-based baseline MLP model and achieves performance comparable to state-of-the-art MLP-based models. This study offers an efficient and effective solution for point cloud classification, balancing performance with computational efficiency.

PointMT: Efficient Point Cloud Analysis with Hybrid MLP-Transformer Architecture

In recent years, point cloud analysis methods based on the Transformer architecture have made significant progress, particularly in the context of multimedia applications such as 3D modeling, virtual reality, and autonomous systems. However, the high computational resource demands of the Transformer architecture hinder its scalability, real-time processing capabilities, and deployment on mobile devices and other platforms with limited computational resources. This limitation remains a significant obstacle to its practical application in scenarios requiring on-device intelligence and multimedia processing. To address this challenge, we propose an efficient point cloud analysis architecture, \textbf{Point} \textbf{M}LP-\textbf{T}ransformer (PointMT). This study tackles the quadratic complexity of the self-attention mechanism by introducing a linear complexity local attention mechanism for effective feature aggregation. Additionally, to counter the Transformer's focus on token differences while neglecting channel differences, we introduce a parameter-free channel temperature adaptation mechanism that adaptively adjusts the attention weight distribution in each channel, enhancing the precision of feature aggregation. To improve the Transformer's slow convergence speed due to the limited scale of point cloud datasets, we propose an MLP-Transformer hybrid module, which significantly enhances the model's convergence speed. Furthermore, to boost the feature representation capability of point tokens, we refine the classification head, enabling point tokens to directly participate in prediction. Experimental results on multiple evaluation benchmarks demonstrate that PointMT achieves performance comparable to state-of-the-art methods while maintaining an optimal balance between performance and accuracy.

PointViG: A Lightweight GNN-based Model for Efficient Point Cloud Analysis

In the domain of point cloud analysis, despite the significant capabilities of Graph Neural Networks (GNNs) in managing complex 3D datasets, existing approaches encounter challenges like high computational costs and scalability issues with extensive scenarios. These limitations restrict the practical deployment of GNNs, notably in resource-constrained environments. To address these issues, this study introduce <b>Point<\b> <b>Vi<\b>sion <b>G<\b>NN (PointViG), an efficient framework for point cloud analysis. PointViG incorporates a lightweight graph convolutional module to efficiently aggregate local features and mitigate over-smoothing. For large-scale point cloud scenes, we propose an adaptive dilated graph convolution technique that searches for sparse neighboring nodes within a dilated neighborhood based on semantic correlation, thereby expanding the receptive field and ensuring computational efficiency. Experiments demonstrate that PointViG achieves performance comparable to state-of-the-art models while balancing performance and complexity. On the ModelNet40 classification task, PointViG achieved 94.3% accuracy with 1.5M parameters. For the S3DIS segmentation task, it achieved an mIoU of 71.7% with 5.3M parameters. These results underscore the potential and efficiency of PointViG in point cloud analysis.

Uncertainty quantification of two-phase flow in porous media via coupled-TgNN surrogate model

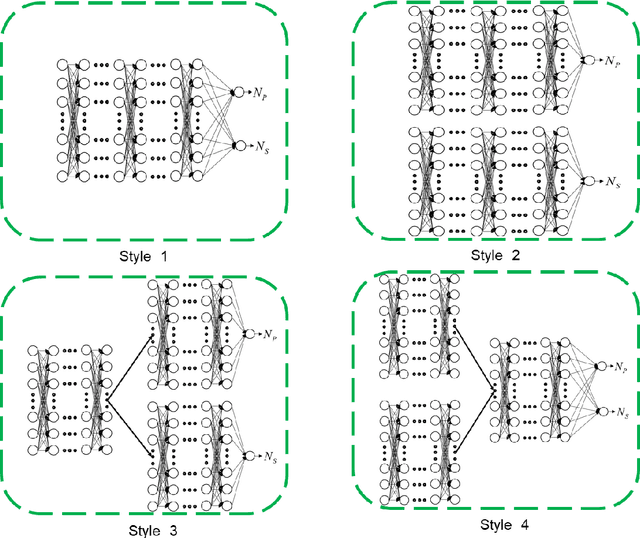
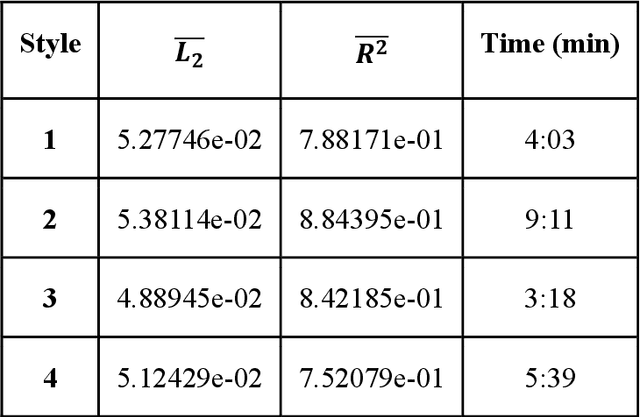
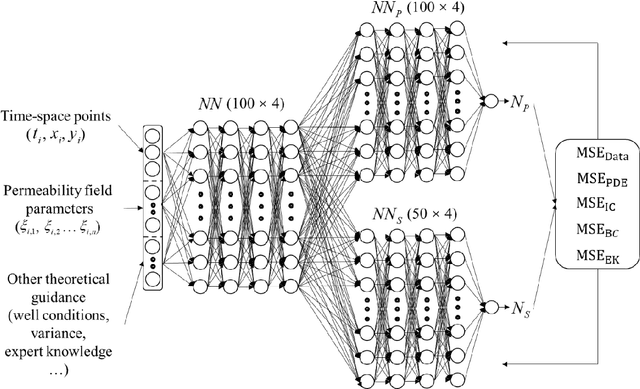
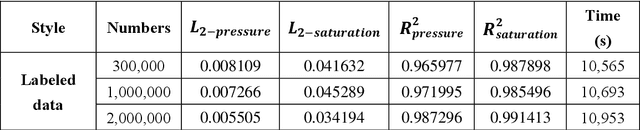
Uncertainty quantification (UQ) of subsurface two-phase flow usually requires numerous executions of forward simulations under varying conditions. In this work, a novel coupled theory-guided neural network (TgNN) based surrogate model is built to facilitate computation efficiency under the premise of satisfactory accuracy. The core notion of this proposed method is to bridge two separate blocks on top of an overall network. They underlie the TgNN model in a coupled form, which reflects the coupling nature of pressure and water saturation in the two-phase flow equation. The TgNN model not only relies on labeled data, but also incorporates underlying scientific theory and experiential rules (e.g., governing equations, stochastic parameter fields, boundary and initial conditions, well conditions, and expert knowledge) as additional components into the loss function. The performance of the TgNN-based surrogate model for two-phase flow problems is tested by different numbers of labeled data and collocation points, as well as the existence of data noise. The proposed TgNN-based surrogate model offers an effective way to solve the coupled nonlinear two-phase flow problem and demonstrates good accuracy and strong robustness when compared with the purely data-driven surrogate model. By combining the accurate TgNN-based surrogate model with the Monte Carlo method, UQ tasks can be performed at a minimum cost to evaluate statistical quantities. Since the heterogeneity of the random fields strongly impacts the results of the surrogate model, corresponding variance and correlation length are added to the input of the neural network to maintain its predictive capacity. The results show that the TgNN-based surrogate model achieves satisfactory accuracy, stability, and efficiency in UQ problems of subsurface two-phase flow.

Inferring electrochemical performance and parameters of Li-ion batteries based on deep operator networks

The Li-ion battery is a complex physicochemical system that generally takes applied current as input and terminal voltage as output. The mappings from current to voltage can be described by several kinds of models, such as accurate but inefficient physics-based models, and efficient but sometimes inaccurate equivalent circuit and black-box models. To realize accuracy and efficiency simultaneously in battery modeling, we propose to build a data-driven surrogate for a battery system while incorporating the underlying physics as constraints. In this work, we innovatively treat the functional mapping from current curve to terminal voltage as a composite of operators, which is approximated by the powerful deep operator network (DeepONet). Its learning capability is firstly verified through a predictive test for Li-ion concentration at two electrodes. In this experiment, the physics-informed DeepONet is found to be more robust than the purely data-driven DeepONet, especially in temporal extrapolation scenarios. A composite surrogate is then constructed for mapping current curve and solid diffusivity to terminal voltage with three operator networks, in which two parallel physics-informed DeepONets are firstly used to predict Li-ion concentration at two electrodes, and then based on their surface values, a DeepONet is built to give terminal voltage predictions. Since the surrogate is differentiable anywhere, it is endowed with the ability to learn from data directly, which was validated by using terminal voltage measurements to estimate input parameters. The proposed surrogate built upon operator networks possesses great potential to be applied in on-board scenarios, such as battery management system, since it integrates efficiency and accuracy by incorporating underlying physics, and also leaves an interface for model refinement through a totally differentiable model structure.

RockGPT: Reconstructing three-dimensional digital rocks from single two-dimensional slice from the perspective of video generation

Random reconstruction of three-dimensional (3D) digital rocks from two-dimensional (2D) slices is crucial for elucidating the microstructure of rocks and its effects on pore-scale flow in terms of numerical modeling, since massive samples are usually required to handle intrinsic uncertainties. Despite remarkable advances achieved by traditional process-based methods, statistical approaches and recently famous deep learning-based models, few works have focused on producing several kinds of rocks with one trained model and allowing the reconstructed samples to satisfy certain given properties, such as porosity. To fill this gap, we propose a new framework, named RockGPT, which is composed of VQ-VAE and conditional GPT, to synthesize 3D samples based on a single 2D slice from the perspective of video generation. The VQ-VAE is utilized to compress high-dimensional input video, i.e., the sequence of continuous rock slices, to discrete latent codes and reconstruct them. In order to obtain diverse reconstructions, the discrete latent codes are modeled using conditional GPT in an autoregressive manner, while incorporating conditional information from a given slice, rock type, and porosity. We conduct two experiments on five kinds of rocks, and the results demonstrate that RockGPT can produce different kinds of rocks with the same model, and the reconstructed samples can successfully meet certain specified porosities. In a broader sense, through leveraging the proposed conditioning scheme, RockGPT constitutes an effective way to build a general model to produce multiple kinds of rocks simultaneously that also satisfy user-defined properties.

Digital rock reconstruction with user-defined properties using conditional generative adversarial networks

Uncertainty is ubiquitous with flow in subsurface rocks because of their inherent heterogeneity and lack of in-situ measurements. To complete uncertainty analysis in a multi-scale manner, it is a prerequisite to provide sufficient rock samples. Even though the advent of digital rock technology offers opportunities to reproduce rocks, it still cannot be utilized to provide massive samples due to its high cost, thus leading to the development of diversified mathematical methods. Among them, two-point statistics (TPS) and multi-point statistics (MPS) are commonly utilized, which feature incorporating low-order and high-order statistical information, respectively. Recently, generative adversarial networks (GANs) are becoming increasingly popular since they can reproduce training images with excellent visual and consequent geologic realism. However, standard GANs can only incorporate information from data, while leaving no interface for user-defined properties, and thus may limit the diversity of reconstructed samples. In this study, we propose conditional GANs for digital rock reconstruction, aiming to reproduce samples not only similar to the real training data, but also satisfying user-specified properties. In fact, the proposed framework can realize the targets of MPS and TPS simultaneously by incorporating high-order information directly from rock images with the GANs scheme, while preserving low-order counterparts through conditioning. We conduct three reconstruction experiments, and the results demonstrate that rock type, rock porosity, and correlation length can be successfully conditioned to affect the reconstructed rock images. Furthermore, in contrast to existing GANs, the proposed conditioning enables learning of multiple rock types simultaneously, and thus invisibly saves the computational cost.

Using Deep Learning to Improve Ensemble Smoother: Applications to Subsurface Characterization

Ensemble smoother (ES) has been widely used in various research fields to reduce the uncertainty of the system-of-interest. However, the commonly-adopted ES method that employs the Kalman formula, that is, ES$_\text{(K)}$, does not perform well when the probability distributions involved are non-Gaussian. To address this issue, we suggest to use deep learning (DL) to derive an alternative update scheme for ES in complex data assimilation applications. Here we show that the DL-based ES method, that is, ES$_\text{(DL)}$, is more general and flexible. In this new update scheme, a high volume of training data are generated from a relatively small-sized ensemble of model parameters and simulation outputs, and possible non-Gaussian features can be preserved in the training data and captured by an adequate DL model. This new variant of ES is tested in two subsurface characterization problems with or without Gaussian assumptions. Results indicate that ES$_\text{(DL)}$ can produce similar (in the Gaussian case) or even better (in the non-Gaussian case) results compared to those from ES$_\text{(K)}$. The success of ES$_\text{(DL)}$ comes from the power of DL in extracting complex (including non-Gaussian) features and learning nonlinear relationships from massive amounts of training data. Although in this work we only apply the ES$_\text{(DL)}$ method in parameter estimation problems, the proposed idea can be conveniently extended to analysis of model structural uncertainty and state estimation in real-time forecasting studies.