Using Deep Learning to Improve Ensemble Smoother: Applications to Subsurface Characterization

Ensemble smoother (ES) has been widely used in various research fields to reduce the uncertainty of the system-of-interest. However, the commonly-adopted ES method that employs the Kalman formula, that is, ES$_\text{(K)}$, does not perform well when the probability distributions involved are non-Gaussian. To address this issue, we suggest to use deep learning (DL) to derive an alternative update scheme for ES in complex data assimilation applications. Here we show that the DL-based ES method, that is, ES$_\text{(DL)}$, is more general and flexible. In this new update scheme, a high volume of training data are generated from a relatively small-sized ensemble of model parameters and simulation outputs, and possible non-Gaussian features can be preserved in the training data and captured by an adequate DL model. This new variant of ES is tested in two subsurface characterization problems with or without Gaussian assumptions. Results indicate that ES$_\text{(DL)}$ can produce similar (in the Gaussian case) or even better (in the non-Gaussian case) results compared to those from ES$_\text{(K)}$. The success of ES$_\text{(DL)}$ comes from the power of DL in extracting complex (including non-Gaussian) features and learning nonlinear relationships from massive amounts of training data. Although in this work we only apply the ES$_\text{(DL)}$ method in parameter estimation problems, the proposed idea can be conveniently extended to analysis of model structural uncertainty and state estimation in real-time forecasting studies.

Physics-informed semantic inpainting: Application to geostatistical modeling

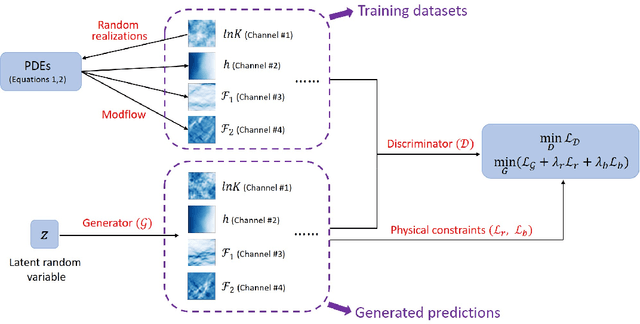
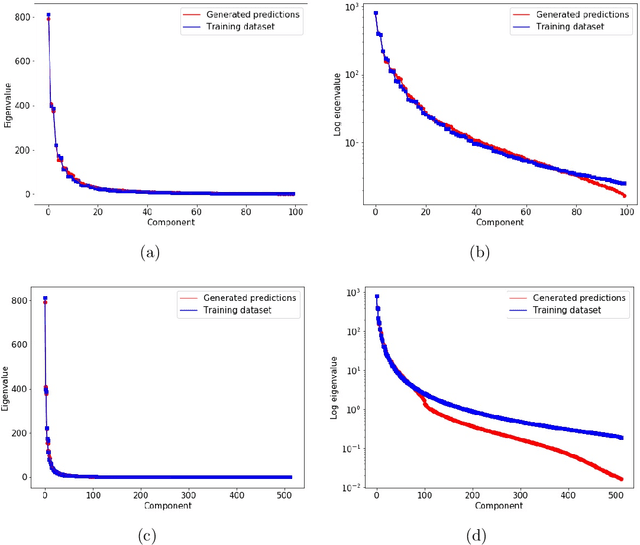
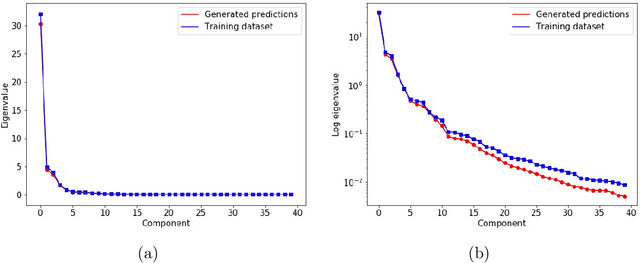
A fundamental problem in geostatistical modeling is to infer the heterogeneous geological field based on limited measurements and some prior spatial statistics. Semantic inpainting, a technique for image processing using deep generative models, has been recently applied for this purpose, demonstrating its effectiveness in dealing with complex spatial patterns. However, the original semantic inpainting framework incorporates only information from direct measurements, while in geostatistics indirect measurements are often plentiful. To overcome this limitation, here we propose a physics-informed semantic inpainting framework, employing the Wasserstein Generative Adversarial Network with Gradient Penalty (WGAN-GP) and jointly incorporating the direct and indirect measurements by exploiting the underlying physical laws. Our simulation results for a high-dimensional problem with 512 dimensions show that in the new method, the physical conservation laws are satisfied and contribute in enhancing the inpainting performance compared to using only the direct measurements.