Deep Learning of Dynamic Subsurface Flow via Theory-guided Generative Adversarial Network
Paper and Code
Jun 02, 2020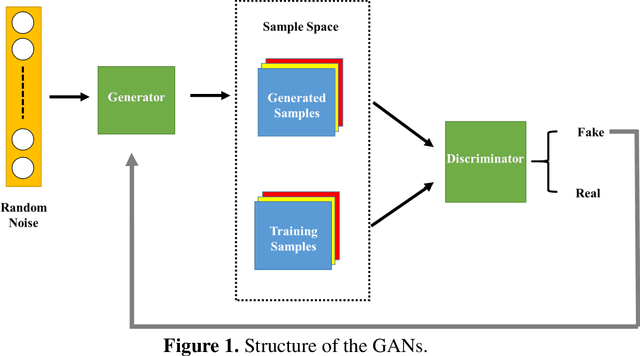

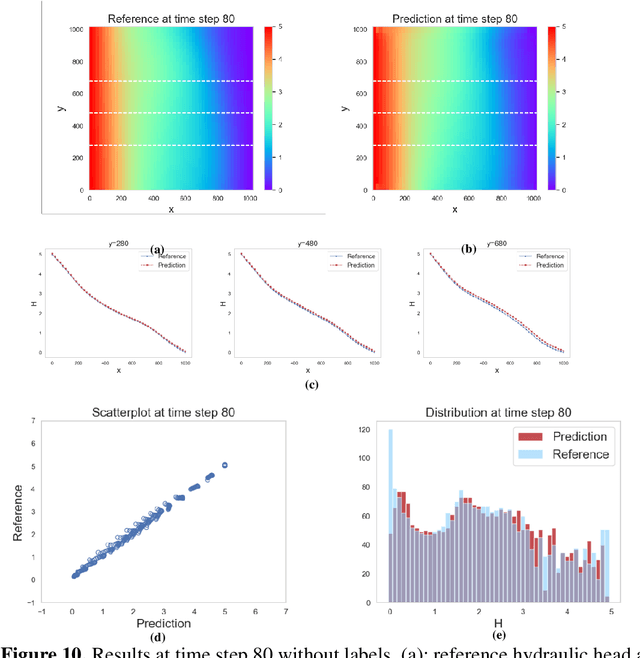

Generative adversarial network (GAN) has been shown to be useful in various applications, such as image recognition, text processing and scientific computing, due its strong ability to learn complex data distributions. In this study, a theory-guided generative adversarial network (TgGAN) is proposed to solve dynamic partial differential equations (PDEs). Different from standard GANs, the training term is no longer the true data and the generated data, but rather their residuals. In addition, such theories as governing equations, other physical constraints and engineering controls, are encoded into the loss function of the generator to ensure that the prediction does not only honor the training data, but also obey these theories. TgGAN is proposed for dynamic subsurface flow with heterogeneous model parameters, and the data at each time step are treated as a two-dimensional image. In this study, several numerical cases are introduced to test the performance of the TgGAN. Predicting the future response, label-free learning and learning from noisy data can be realized easily by the TgGAN model. The effects of the number of training data and the collocation points are also discussed. In order to improve the efficiency of TgGAN, the transfer learning algorithm is also employed. Numerical results demonstrate that the TgGAN model is robust and reliable for deep learning of dynamic PDEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge