Weak Form Theory-guided Neural Network for Deep Learning of Subsurface Single and Two-phase Flow

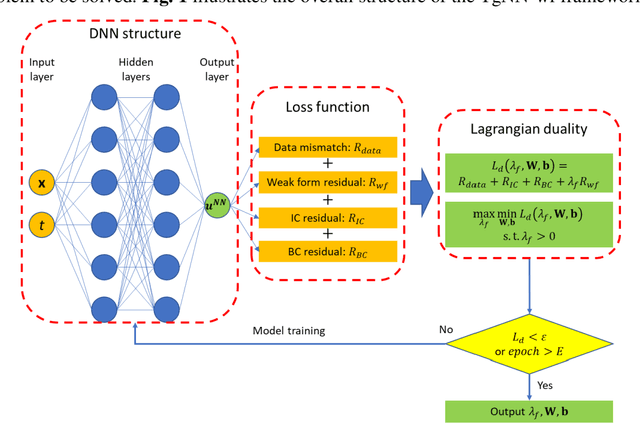
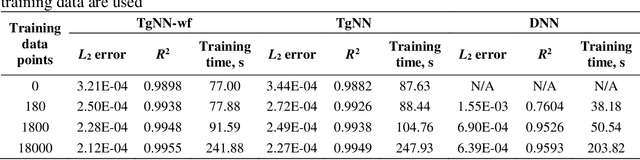
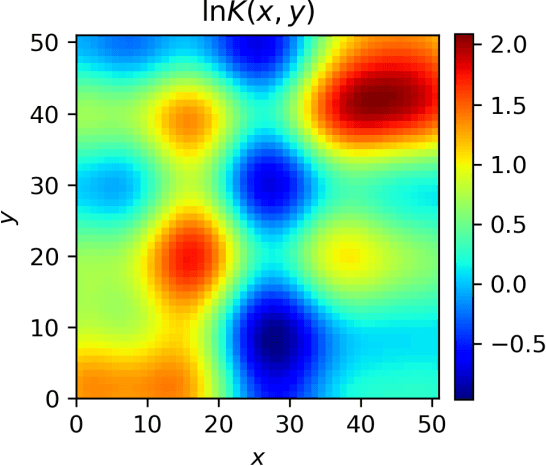
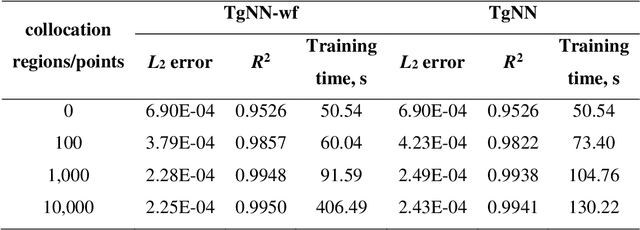
Deep neural networks (DNNs) are widely used as surrogate models in geophysical applications; incorporating theoretical guidance into DNNs has improved the generalizability. However, most of such approaches define the loss function based on the strong form of conservation laws (via partial differential equations, PDEs), which is subject to deteriorated accuracy when the PDE has high order derivatives or the solution has strong discontinuities. Herein, we propose a weak form theory-guided neural network (TgNN-wf), which incorporates the weak form formulation of the PDE into the loss function combined with data constraint and initial and boundary conditions regularizations to tackle the aforementioned difficulties. In the weak form, high order derivatives in the PDE can be transferred to the test functions by performing integration-by-parts, which reduces computational error. We use domain decomposition with locally defined test functions, which captures local discontinuity effectively. Two numerical cases demonstrate the superiority of the proposed TgNN-wf over the strong form TgNN, including the hydraulic head prediction for unsteady-state 2D single-phase flow problems and the saturation profile prediction for 1D two-phase flow problems. Results show that TgNN-wf consistently has higher accuracy than TgNN, especially when strong discontinuity in the solution is present. TgNN-wf also trains faster than TgNN when the number of integration subdomains is not too large (<10,000). Moreover, TgNN-wf is more robust to noises. Thus, the proposed TgNN-wf paves the way for which a variety of deep learning problems in the small data regime can be solved more accurately and efficiently.

A Lagrangian Dual-based Theory-guided Deep Neural Network

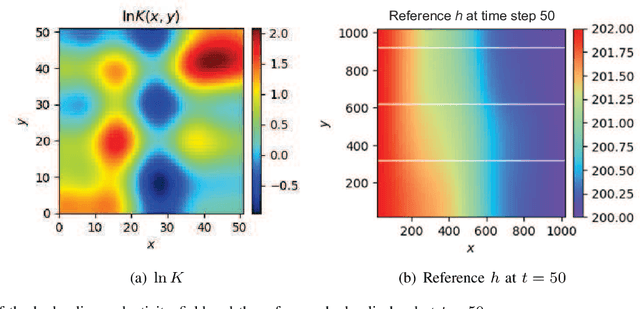
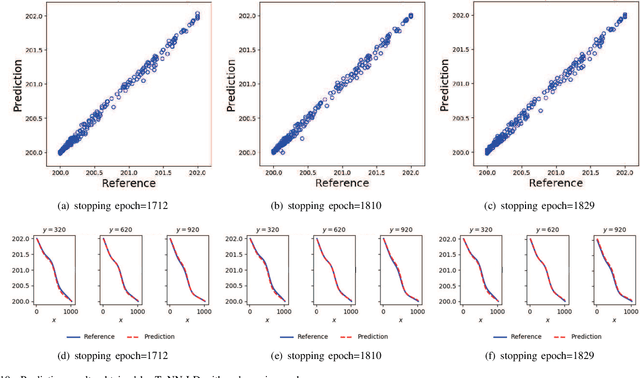
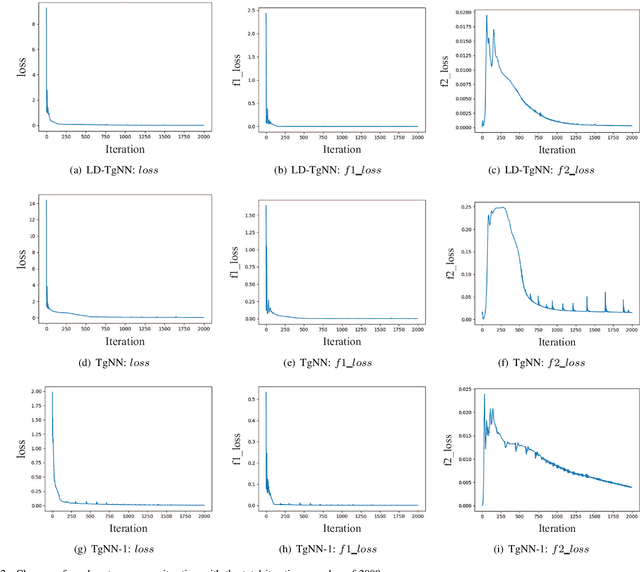
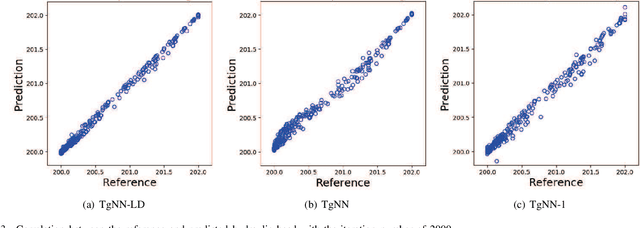
The theory-guided neural network (TgNN) is a kind of method which improves the effectiveness and efficiency of neural network architectures by incorporating scientific knowledge or physical information. Despite its great success, the theory-guided (deep) neural network possesses certain limits when maintaining a tradeoff between training data and domain knowledge during the training process. In this paper, the Lagrangian dual-based TgNN (TgNN-LD) is proposed to improve the effectiveness of TgNN. We convert the original loss function into a constrained form with fewer items, in which partial differential equations (PDEs), engineering controls (ECs), and expert knowledge (EK) are regarded as constraints, with one Lagrangian variable per constraint. These Lagrangian variables are incorporated to achieve an equitable tradeoff between observation data and corresponding constraints, in order to improve prediction accuracy, and conserve time and computational resources adjusted by an ad-hoc procedure. To investigate the performance of the proposed method, the original TgNN model with a set of optimized weight values adjusted by ad-hoc procedures is compared on a subsurface flow problem, with their L2 error, R square (R2), and computational time being analyzed. Experimental results demonstrate the superiority of the Lagrangian dual-based TgNN.