GFlowOut: Dropout with Generative Flow Networks

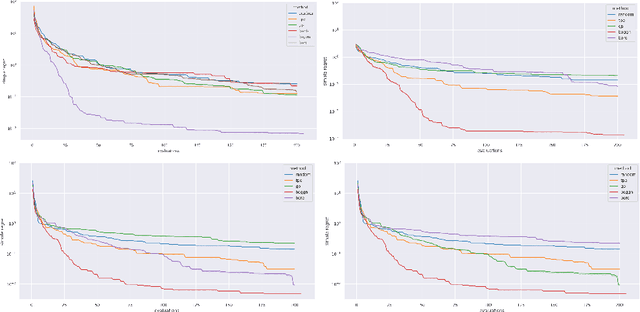
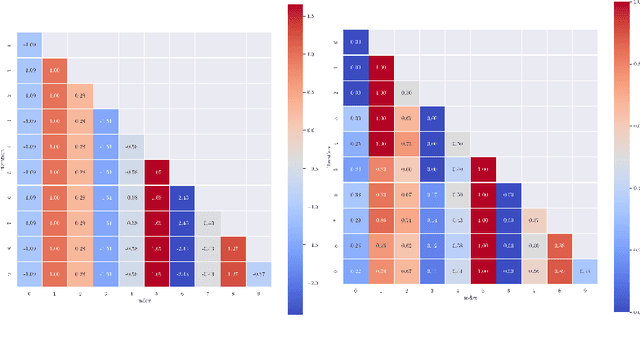
Bayesian Inference offers principled tools to tackle many critical problems with modern neural networks such as poor calibration and generalization, and data inefficiency. However, scaling Bayesian inference to large architectures is challenging and requires restrictive approximations. Monte Carlo Dropout has been widely used as a relatively cheap way for approximate Inference and to estimate uncertainty with deep neural networks. Traditionally, the dropout mask is sampled independently from a fixed distribution. Recent works show that the dropout mask can be viewed as a latent variable, which can be inferred with variational inference. These methods face two important challenges: (a) the posterior distribution over masks can be highly multi-modal which can be difficult to approximate with standard variational inference and (b) it is not trivial to fully utilize sample-dependent information and correlation among dropout masks to improve posterior estimation. In this work, we propose GFlowOut to address these issues. GFlowOut leverages the recently proposed probabilistic framework of Generative Flow Networks (GFlowNets) to learn the posterior distribution over dropout masks. We empirically demonstrate that GFlowOut results in predictive distributions that generalize better to out-of-distribution data, and provide uncertainty estimates which lead to better performance in downstream tasks.

Approximate Bayesian Optimisation for Neural Networks

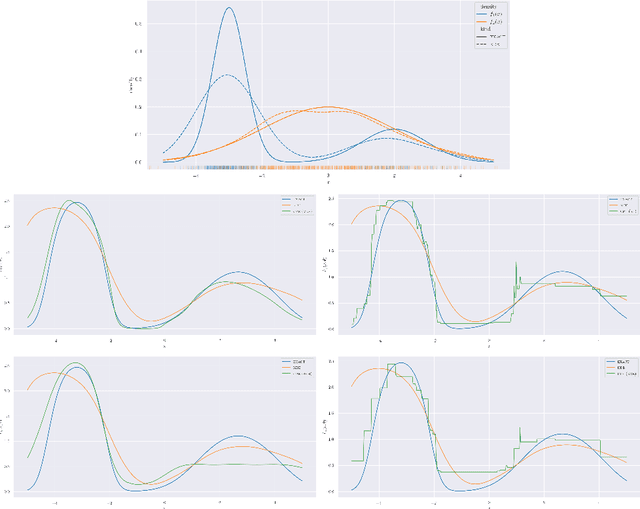
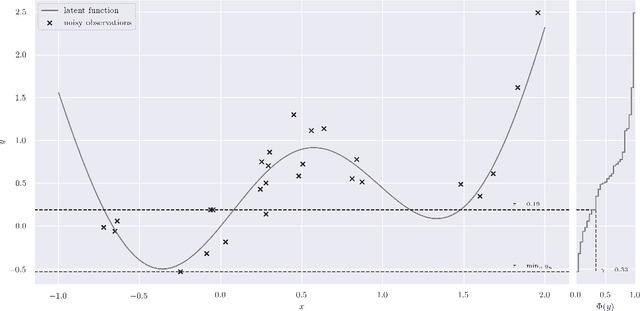
A body of work has been done to automate machine learning algorithm to highlight the importance of model choice. Automating the process of choosing the best forecasting model and its corresponding parameters can result to improve a wide range of real-world applications. Bayesian optimisation (BO) uses a blackbox optimisation methods to propose solutions according to an exploration-exploitation trade-off criterion through acquisition functions. BO framework imposes two key ingredients: a probabilistic surrogate model that consist of prior belief of the unknown objective function(data-dependant) and an objective function that describes how optimal is the model-fit. Choosing the best model and its associated hyperparameters can be very expensive, and is typically fit using Gaussian processes (GPs) and at some extends applying approximate inference due its intractability. However, since GPs scale cubically with the number of observations, it has been challenging to handle objectives whose optimization requires many evaluations. In addition, most real-dataset are non-stationary which make idealistic assumptions on surrogate models. The necessity to solve the analytical tractability and the computational feasibility in a stochastic fashion enables to ensure the efficiency and the applicability of Bayesian optimisation. In this paper we explore the use of neural networks as an alternative to GPs to model distributions over functions, we provide a link between density-ratio estimation and class probability estimation based on approximate inference, this reformulation provides algorithm efficiency and tractability.