Efficient Certified Training and Robustness Verification of Neural ODEs

Neural Ordinary Differential Equations (NODEs) are a novel neural architecture, built around initial value problems with learned dynamics which are solved during inference. Thought to be inherently more robust against adversarial perturbations, they were recently shown to be vulnerable to strong adversarial attacks, highlighting the need for formal guarantees. However, despite significant progress in robustness verification for standard feed-forward architectures, the verification of high dimensional NODEs remains an open problem. In this work, we address this challenge and propose GAINS, an analysis framework for NODEs combining three key ideas: (i) a novel class of ODE solvers, based on variable but discrete time steps, (ii) an efficient graph representation of solver trajectories, and (iii) a novel abstraction algorithm operating on this graph representation. Together, these advances enable the efficient analysis and certified training of high-dimensional NODEs, by reducing the runtime from an intractable $O(\exp(d)+\exp(T))$ to ${O}(d+T^2 \log^2T)$ in the dimensionality $d$ and integration time $T$. In an extensive evaluation on computer vision (MNIST and FMNIST) and time-series forecasting (PHYSIO-NET) problems, we demonstrate the effectiveness of both our certified training and verification methods.

Remember and Forget Experience Replay for Multi-Agent Reinforcement Learning

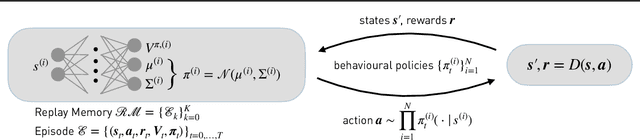
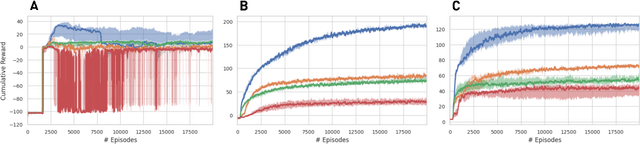
We present the extension of the Remember and Forget for Experience Replay (ReF-ER) algorithm to Multi-Agent Reinforcement Learning (MARL). {ReF-ER} was shown to outperform state of the art algorithms for continuous control in problems ranging from the OpenAI Gym to complex fluid flows. In MARL, the dependencies between the agents are included in the state-value estimator and the environment dynamics are modeled via the importance weights used by ReF-ER. In collaborative environments, we find the best performance when the value is estimated using individual rewards and we ignore the effects of other actions on the transition map. We benchmark the performance of ReF-ER MARL on the Stanford Intelligent Systems Laboratory (SISL) environments. We find that employing a single feed-forward neural network for the policy and the value function in ReF-ER MARL, outperforms state of the art algorithms that rely on complex neural network architectures.

A Neuro-vector-symbolic Architecture for Solving Raven's Progressive Matrices

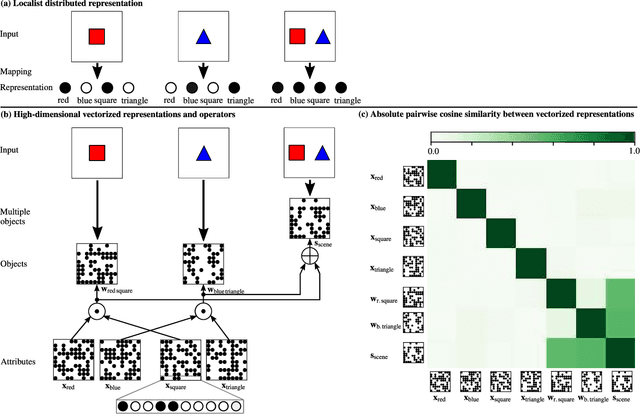
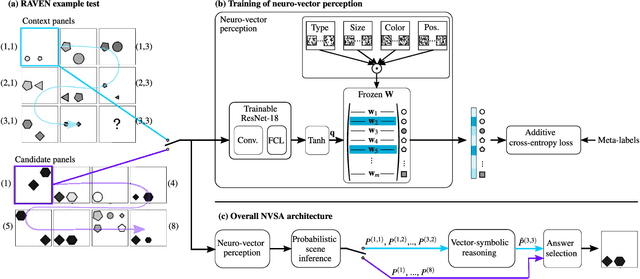
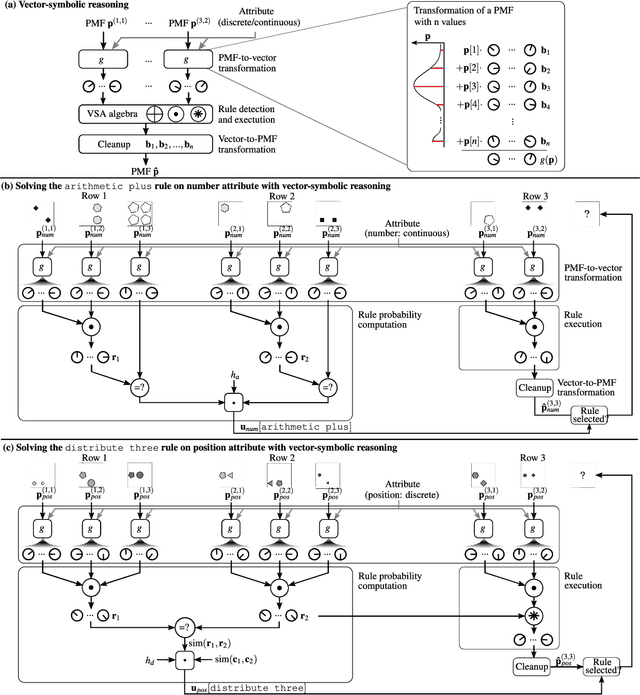
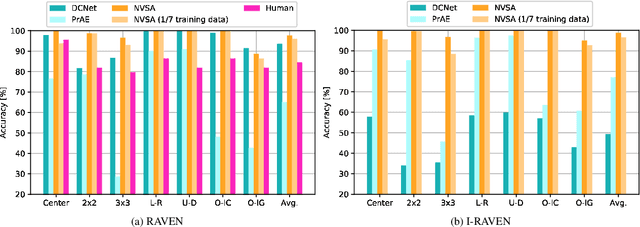
Neither deep neural networks nor symbolic AI alone have approached the kind of intelligence expressed in humans. This is mainly because neural networks are not able to decompose distinct objects from their joint representation (the so-called binding problem), while symbolic AI suffers from exhaustive rule searches, among other problems. These two problems are still pronounced in neuro-symbolic AI which aims to combine the best of the two paradigms. Here, we show that the two problems can be addressed with our proposed neuro-vector-symbolic architecture (NVSA) by exploiting its powerful operators on fixed-width holographic vectorized representations that serve as a common language between neural networks and symbolic logical reasoning. The efficacy of NVSA is demonstrated by solving the Raven's progressive matrices. NVSA achieves a new record of 97.7% average accuracy in RAVEN, and 98.8% in I-RAVEN datasets, with two orders of magnitude faster execution than the symbolic logical reasoning on CPUs.