Dementia Severity Classification under Small Sample Size and Weak Supervision in Thick Slice MRI

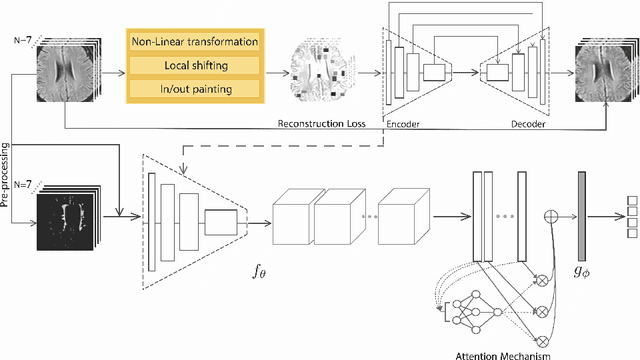
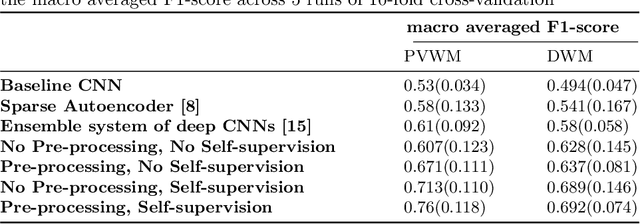
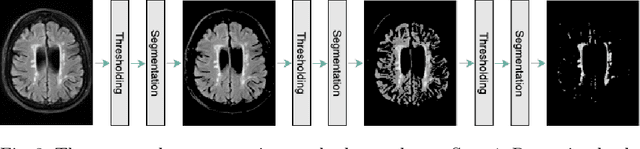
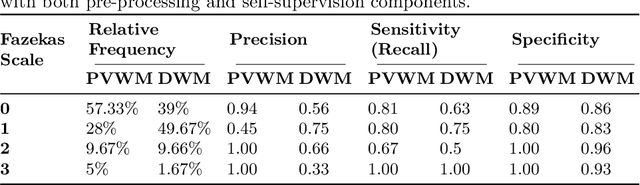
Early detection of dementia through specific biomarkers in MR images plays a critical role in developing support strategies proactively. Fazekas scale facilitates an accurate quantitative assessment of the severity of white matter lesions and hence the disease. Imaging Biomarkers of dementia are multiple and comprehensive documentation of them is time-consuming. Therefore, any effort to automatically extract these biomarkers will be of clinical value while reducing inter-rater discrepancies. To tackle this problem, we propose to classify the disease severity based on the Fazekas scale through the visual biomarkers, namely the Periventricular White Matter (PVWM) and the Deep White Matter (DWM) changes, in the real-world setting of thick-slice MRI. Small training sample size and weak supervision in form of assigning severity labels to the whole MRI stack are among the main challenges. To combat the mentioned issues, we have developed a deep learning pipeline that employs self-supervised representation learning, multiple instance learning, and appropriate pre-processing steps. We use pretext tasks such as non-linear transformation, local shuffling, in- and out-painting for self-supervised learning of useful features in this domain. Furthermore, an attention model is used to determine the relevance of each MRI slice for predicting the Fazekas scale in an unsupervised manner. We show the significant superiority of our method in distinguishing different classes of dementia compared to state-of-the-art methods in our mentioned setting, which improves the macro averaged F1-score of state-of-the-art from 61% to 76% in PVWM, and from 58% to 69.2% in DWM.

Active Learning from Positive and Unlabeled Data

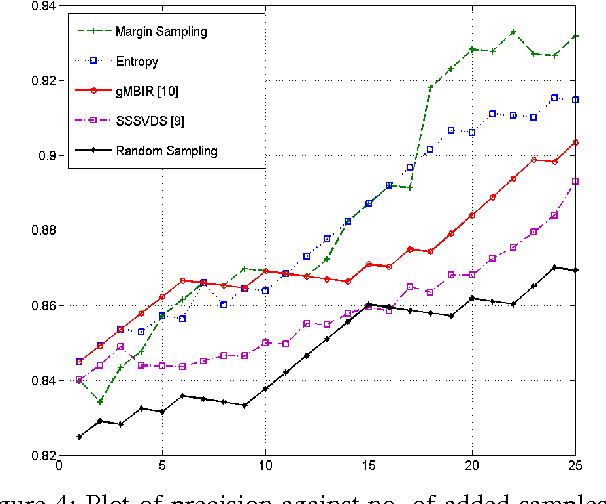
During recent years, active learning has evolved into a popular paradigm for utilizing user's feedback to improve accuracy of learning algorithms. Active learning works by selecting the most informative sample among unlabeled data and querying the label of that point from user. Many different methods such as uncertainty sampling and minimum risk sampling have been utilized to select the most informative sample in active learning. Although many active learning algorithms have been proposed so far, most of them work with binary or multi-class classification problems and therefore can not be applied to problems in which only samples from one class as well as a set of unlabeled data are available. Such problems arise in many real-world situations and are known as the problem of learning from positive and unlabeled data. In this paper we propose an active learning algorithm that can work when only samples of one class as well as a set of unlabelled data are available. Our method works by separately estimating probability desnity of positive and unlabeled points and then computing expected value of informativeness to get rid of a hyper-parameter and have a better measure of informativeness./ Experiments and empirical analysis show promising results compared to other similar methods.

Minimax Optimal Sparse Signal Recovery with Poisson Statistics

We are motivated by problems that arise in a number of applications such as Online Marketing and Explosives detection, where the observations are usually modeled using Poisson statistics. We model each observation as a Poisson random variable whose mean is a sparse linear superposition of known patterns. Unlike many conventional problems observations here are not identically distributed since they are associated with different sensing modalities. We analyze the performance of a Maximum Likelihood (ML) decoder, which for our Poisson setting involves a non-linear optimization but yet is computationally tractable. We derive fundamental sample complexity bounds for sparse recovery when the measurements are contaminated with Poisson noise. In contrast to the least-squares linear regression setting with Gaussian noise, we observe that in addition to sparsity, the scale of the parameters also fundamentally impacts $\ell_2$ error in the Poisson setting. We show tightness of our upper bounds both theoretically and experimentally. In particular, we derive a minimax matching lower bound on the mean-squared error and show that our constrained ML decoder is minimax optimal for this regime.

Necessary and Sufficient Conditions for Novel Word Detection in Separable Topic Models

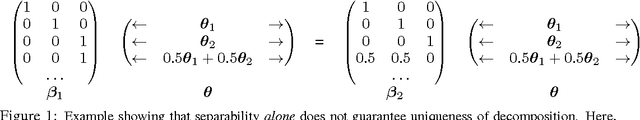
The simplicial condition and other stronger conditions that imply it have recently played a central role in developing polynomial time algorithms with provable asymptotic consistency and sample complexity guarantees for topic estimation in separable topic models. Of these algorithms, those that rely solely on the simplicial condition are impractical while the practical ones need stronger conditions. In this paper, we demonstrate, for the first time, that the simplicial condition is a fundamental, algorithm-independent, information-theoretic necessary condition for consistent separable topic estimation. Furthermore, under solely the simplicial condition, we present a practical quadratic-complexity algorithm based on random projections which consistently detects all novel words of all topics using only up to second-order empirical word moments. This algorithm is amenable to distributed implementation making it attractive for 'big-data' scenarios involving a network of large distributed databases.

Topic Discovery through Data Dependent and Random Projections

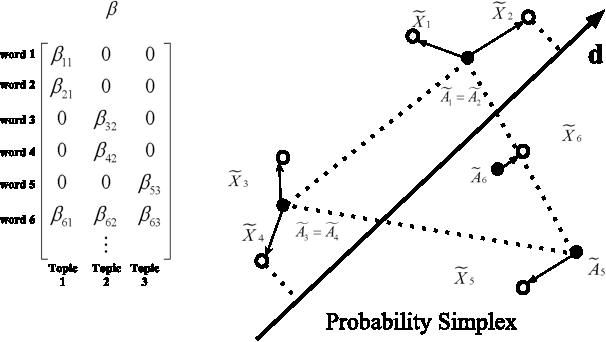
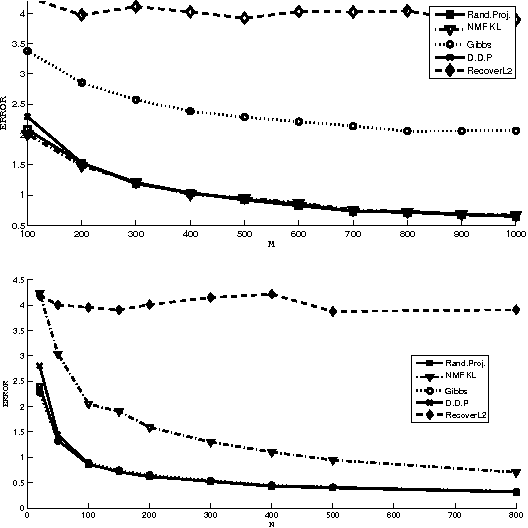
We present algorithms for topic modeling based on the geometry of cross-document word-frequency patterns. This perspective gains significance under the so called separability condition. This is a condition on existence of novel-words that are unique to each topic. We present a suite of highly efficient algorithms based on data-dependent and random projections of word-frequency patterns to identify novel words and associated topics. We will also discuss the statistical guarantees of the data-dependent projections method based on two mild assumptions on the prior density of topic document matrix. Our key insight here is that the maximum and minimum values of cross-document frequency patterns projected along any direction are associated with novel words. While our sample complexity bounds for topic recovery are similar to the state-of-art, the computational complexity of our random projection scheme scales linearly with the number of documents and the number of words per document. We present several experiments on synthetic and real-world datasets to demonstrate qualitative and quantitative merits of our scheme.

A New Geometric Approach to Latent Topic Modeling and Discovery

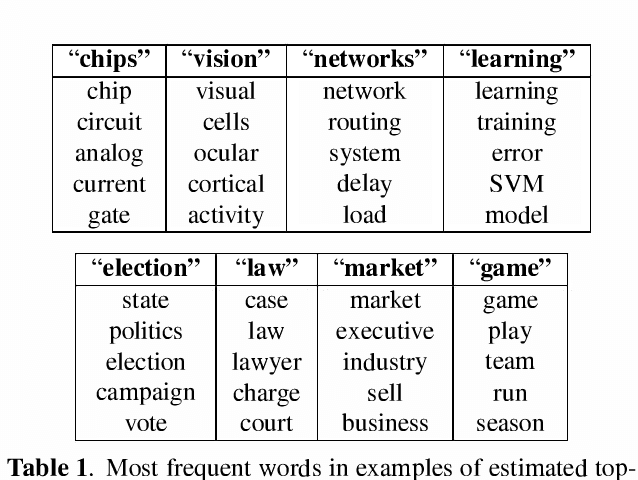
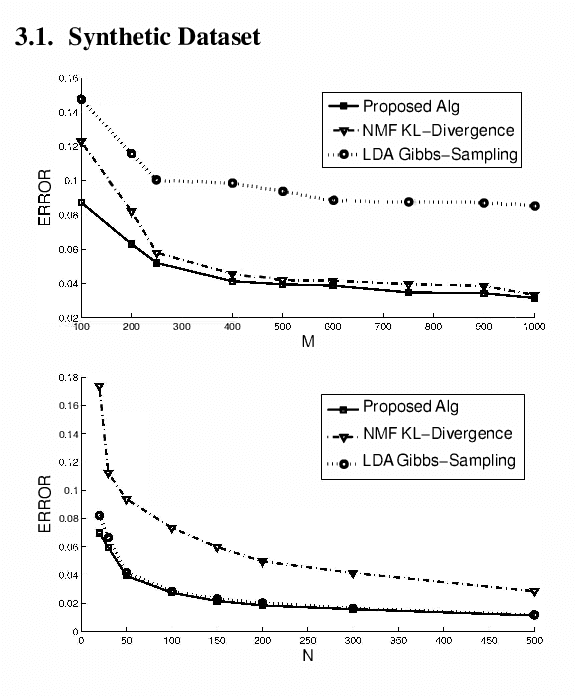
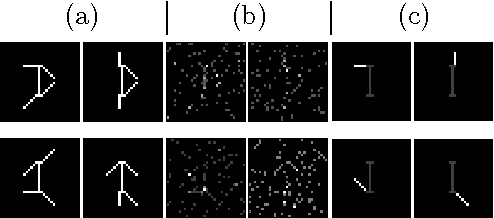
A new geometrically-motivated algorithm for nonnegative matrix factorization is developed and applied to the discovery of latent "topics" for text and image "document" corpora. The algorithm is based on robustly finding and clustering extreme points of empirical cross-document word-frequencies that correspond to novel "words" unique to each topic. In contrast to related approaches that are based on solving non-convex optimization problems using suboptimal approximations, locally-optimal methods, or heuristics, the new algorithm is convex, has polynomial complexity, and has competitive qualitative and quantitative performance compared to the current state-of-the-art approaches on synthetic and real-world datasets.