Mirco Pezzoli
Phase-Retrieval-Based Physics-Informed Neural Networks For Acoustic Magnitude Field Reconstruction
Jan 27, 2026Abstract:We propose a method for estimating the magnitude distribution of an acoustic field from spatially sparse magnitude measurements. Such a method is useful when phase measurements are unreliable or inaccessible. Physics-informed neural networks (PINNs) have shown promise for sound field estimation by incorporating constraints derived from governing partial differential equations (PDEs) into neural networks. However, they do not extend to settings where phase measurements are unavailable, as the loss function based on the governing PDE relies on phase information. To remedy this, we propose a phase-retrieval-based PINN for magnitude field estimation. By representing the magnitude and phase distributions with separate networks, the PDE loss can be computed based on the reconstructed complex amplitude. We demonstrate the effectiveness of our phase-retrieval-based PINN through experimental evaluation.
Physics-Informed Neural Network-Driven Sparse Field Discretization Method for Near-Field Acoustic Holography
May 01, 2025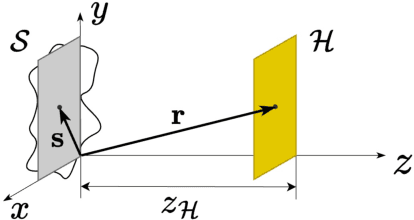
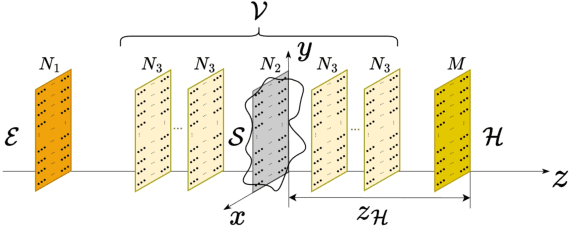
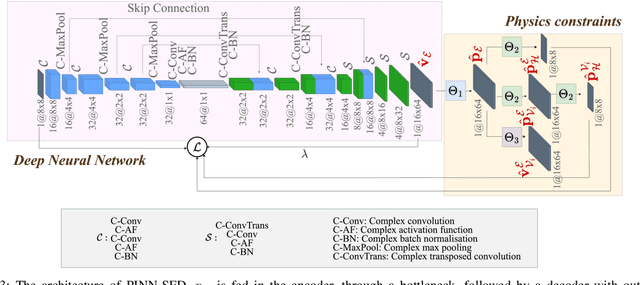
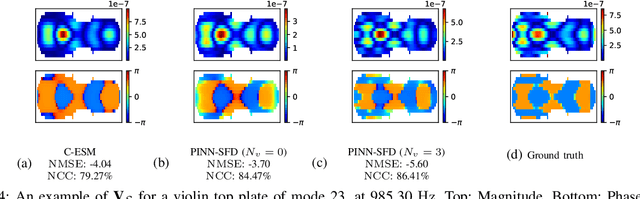
Abstract:We propose the Physics-Informed Neural Network-driven Sparse Field Discretization method (PINN-SFD), a novel self-supervised, physics-informed deep learning approach for addressing the Near-Field Acoustic Holography (NAH) problem. Unlike existing deep learning methods for NAH, which are predominantly supervised by large datasets, our approach does not require a training phase and it is physics-informed. The wave propagation field is discretized into sparse regions, a process referred to as field discretization, which includes a series of set of source planes, to address the inverse problem. Our method employs the discretized Kirchhoff-Helmholtz integral as the wave propagation model. By incorporating virtual planes, additional constraints are enforced near the actual sound source, improving the reconstruction process. Optimization is carried out using Physics-Informed Neural Networks (PINNs), where physics-based constraints are integrated into the loss functions to account for both direct (from equivalent source plane to hologram plane) and additional (from virtual planes to hologram plane) wave propagation paths. Additionally, sparsity is enforced on the velocity of the equivalent sources. Our comprehensive validation across various rectangular and violin top plates, covering a wide range of vibrational modes, demonstrates that PINN-SFD consistently outperforms the conventional Compressive-Equivalent Source Method (C-ESM), particularly in terms of reconstruction accuracy for complex vibrational patterns. Significantly, this method demonstrates reduced sensitivity to regularization parameters compared to C-ESM.
DiffusionRIR: Room Impulse Response Interpolation using Diffusion Models
Apr 29, 2025Abstract:Room Impulse Responses (RIRs) characterize acoustic environments and are crucial in multiple audio signal processing tasks. High-quality RIR estimates drive applications such as virtual microphones, sound source localization, augmented reality, and data augmentation. However, obtaining RIR measurements with high spatial resolution is resource-intensive, making it impractical for large spaces or when dense sampling is required. This research addresses the challenge of estimating RIRs at unmeasured locations within a room using Denoising Diffusion Probabilistic Models (DDPM). Our method leverages the analogy between RIR matrices and image inpainting, transforming RIR data into a format suitable for diffusion-based reconstruction. Using simulated RIR data based on the image method, we demonstrate our approach's effectiveness on microphone arrays of different curvatures, from linear to semi-circular. Our method successfully reconstructs missing RIRs, even in large gaps between microphones. Under these conditions, it achieves accurate reconstruction, significantly outperforming baseline Spline Cubic Interpolation in terms of Normalized Mean Square Error and Cosine Distance between actual and interpolated RIRs. This research highlights the potential of using generative models for effective RIR interpolation, paving the way for generating additional data from limited real-world measurements.
Towards HRTF Personalization using Denoising Diffusion Models
Jan 06, 2025
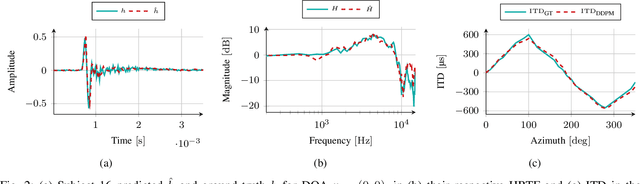
Abstract:Head-Related Transfer Functions (HRTFs) have fundamental applications for realistic rendering in immersive audio scenarios. However, they are strongly subject-dependent as they vary considerably depending on the shape of the ears, head and torso. Thus, personalization procedures are required for accurate binaural rendering. Recently, Denoising Diffusion Probabilistic Models (DDPMs), a class of generative learning techniques, have been applied to solve a variety of signal processing-related problems. In this paper, we propose a first approach for using DDPM conditioned on anthropometric measurements to generate personalized Head-Related Impulse Response (HRIR), the time-domain representation of HRTF. The results show the feasibility of DDPMs for HRTF personalization obtaining performance in line with state-of-the-art models.
A Zero-Shot Physics-Informed Dictionary Learning Approach for Sound Field Reconstruction
Dec 24, 2024


Abstract:Sound field reconstruction aims to estimate pressure fields in areas lacking direct measurements. Existing techniques often rely on strong assumptions or face challenges related to data availability or the explicit modeling of physical properties. To bridge these gaps, this study introduces a zero-shot, physics-informed dictionary learning approach to perform sound field reconstruction. Our method relies only on a few sparse measurements to learn a dictionary, without the need for additional training data. Moreover, by enforcing the Helmholtz equation during the optimization process, the proposed approach ensures that the reconstructed sound field is represented as a linear combination of a few physically meaningful atoms. Evaluations on real-world data show that our approach achieves comparable performance to state-of-the-art dictionary learning techniques, with the advantage of requiring only a few observations of the sound field and no training on a dataset.
Physics-Informed Machine Learning For Sound Field Estimation
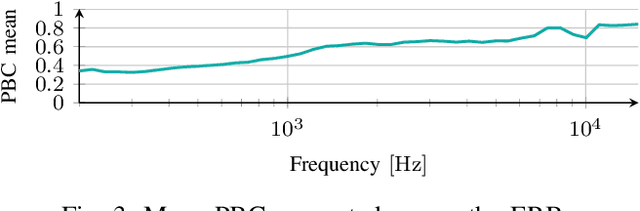
Aug 27, 2024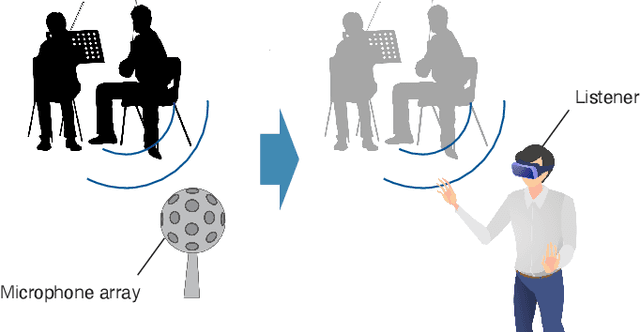
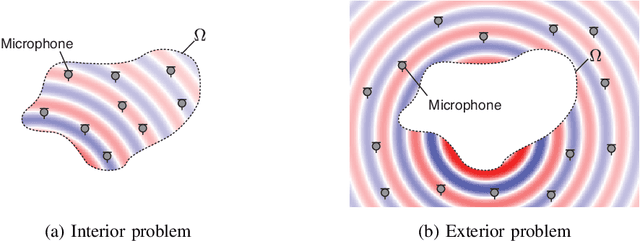
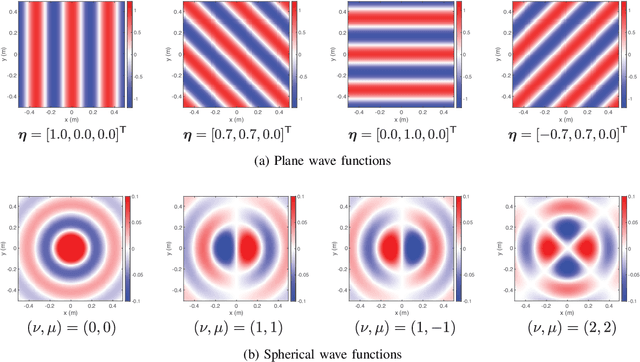
Abstract:The area of study concerning the estimation of spatial sound, i.e., the distribution of a physical quantity of sound such as acoustic pressure, is called sound field estimation, which is the basis for various applied technologies related to spatial audio processing. The sound field estimation problem is formulated as a function interpolation problem in machine learning in a simplified scenario. However, high estimation performance cannot be expected by simply applying general interpolation techniques that rely only on data. The physical properties of sound fields are useful a priori information, and it is considered extremely important to incorporate them into the estimation. In this article, we introduce the fundamentals of physics-informed machine learning (PIML) for sound field estimation and overview current PIML-based sound field estimation methods.
A Physics-Informed Neural Network-Based Approach for the Spatial Upsampling of Spherical Microphone Arrays
Jul 26, 2024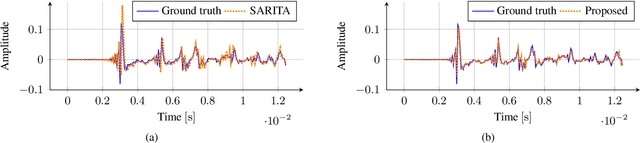
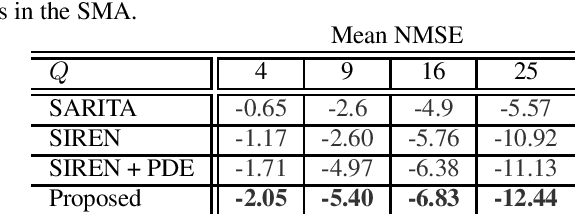
Abstract:Spherical microphone arrays are convenient tools for capturing the spatial characteristics of a sound field. However, achieving superior spatial resolution requires arrays with numerous capsules, consequently leading to expensive devices. To address this issue, we present a method for spatially upsampling spherical microphone arrays with a limited number of capsules. Our approach exploits a physics-informed neural network with Rowdy activation functions, leveraging physical constraints to provide high-order microphone array signals, starting from low-order devices. Results show that, within its domain of application, our approach outperforms a state of the art method based on signal processing for spherical microphone arrays upsampling.
Physics-Informed Neural Network for Volumetric Sound field Reconstruction of Speech Signals
Mar 14, 2024Abstract:Recent developments in acoustic signal processing have seen the integration of deep learning methodologies, alongside the continued prominence of classical wave expansion-based approaches, particularly in sound field reconstruction. Physics-Informed Neural Networks (PINNs) have emerged as a novel framework, bridging the gap between data-driven and model-based techniques for addressing physical phenomena governed by partial differential equations. This paper introduces a PINN-based approach for the recovery of arbitrary volumetric acoustic fields. The network incorporates the wave equation to impose a regularization on signal reconstruction in the time domain. This methodology enables the network to learn the underlying physics of sound propagation and allows for the complete characterization of the sound field based on a limited set of observations. The proposed method's efficacy is validated through experiments involving speech signals in a real-world environment, considering varying numbers of available measurements. Moreover, a comparative analysis is undertaken against state-of-the-art frequency-domain and time-domain reconstruction methods from existing literature, highlighting the increased accuracy across the various measurement configurations.
HOMULA-RIR: A Room Impulse Response Dataset for Teleconferencing and Spatial Audio Applications Acquired Through Higher-Order Microphones and Uniform Linear Microphone Arrays
Feb 21, 2024
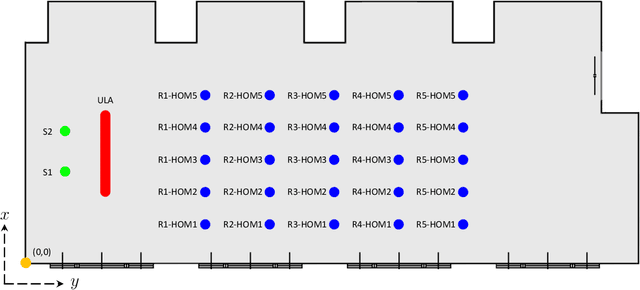
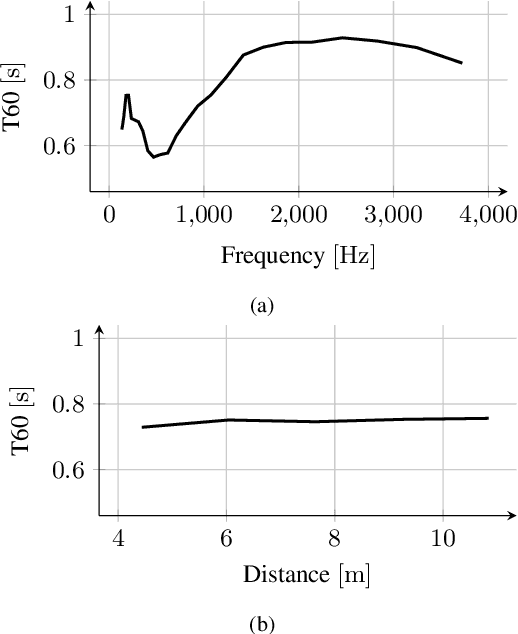
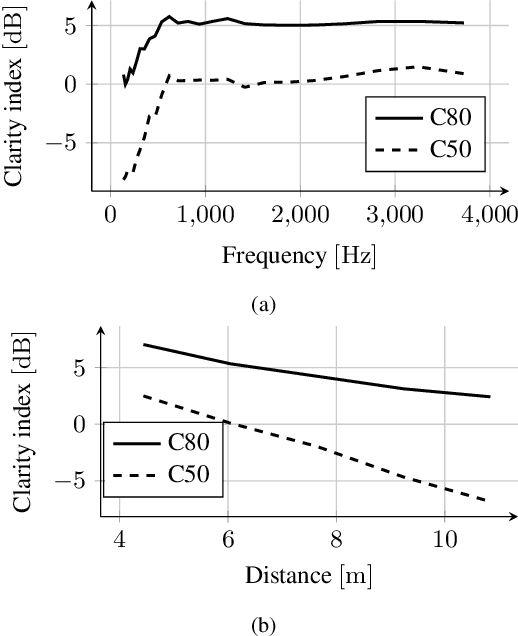
Abstract:In this paper, we present HOMULA-RIR, a dataset of room impulse responses (RIRs) acquired using both higher-order microphones (HOMs) and a uniform linear array (ULA), in order to model a remote attendance teleconferencing scenario. Specifically, measurements were performed in a seminar room, where a 64-microphone ULA was used as a multichannel audio acquisition system in the proximity of the speakers, while HOMs were used to model 25 attendees actually present in the seminar room. The HOMs cover a wide area of the room, making the dataset suitable also for applications of virtual acoustics. Through the measurement of the reverberation time and clarity index, and sample applications such as source localization and separation, we demonstrate the effectiveness of the HOMULA-RIR dataset.
Room transfer function reconstruction using complex-valued neural networks and irregularly distributed microphones
Feb 01, 2024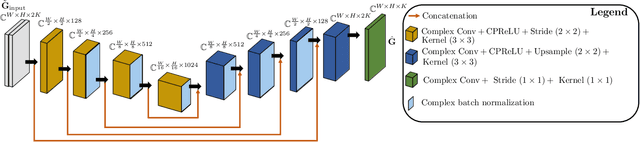
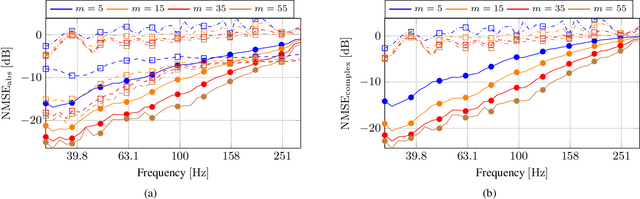
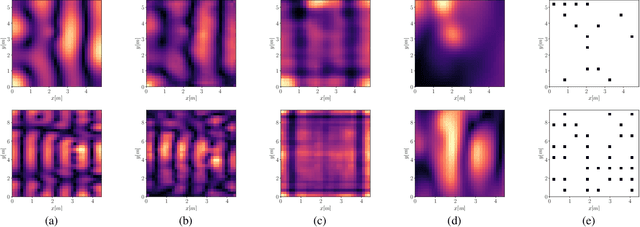
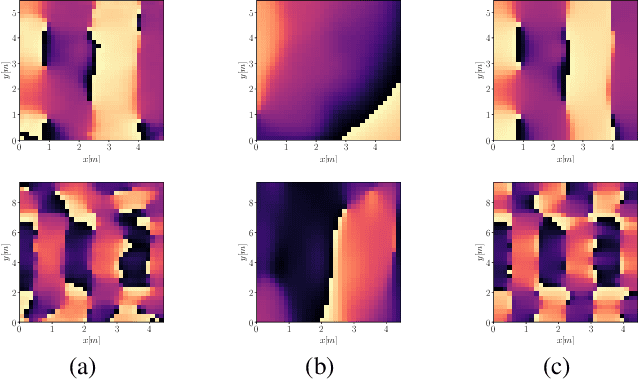
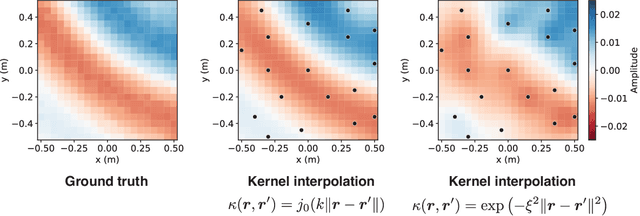
Abstract:Reconstructing the room transfer functions needed to calculate the complex sound field in a room has several important real-world applications. However, an unpractical number of microphones is often required. Recently, in addition to classical signal processing methods, deep learning techniques have been applied to reconstruct the room transfer function starting from a very limited set of room transfer functions measured at scattered points in the room. In this study, we employ complex-valued neural networks to estimate room transfer functions in the frequency range of the first room resonances, using a few irregularly distributed microphones. To the best of our knowledge, this is the first time complex-valued neural networks are used to estimate room transfer functions. To analyze the benefits of applying complex-valued optimization to the considered task, we compare the proposed technique with a state-of-the-art real-valued neural network method and a state-of-the-art kernel-based signal processing approach for sound field reconstruction, showing that the proposed technique exhibits relevant advantages in terms of phase accuracy and overall quality of the reconstructed sound field.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge