Physics-Informed Machine Learning For Sound Field Estimation

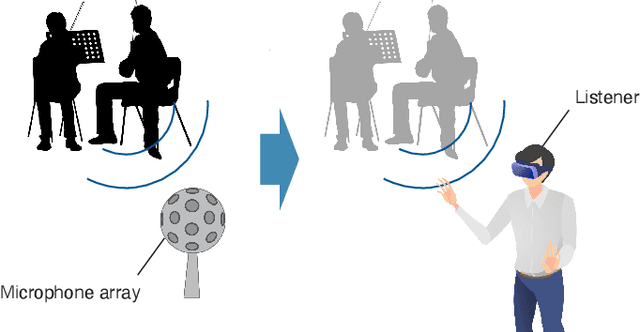
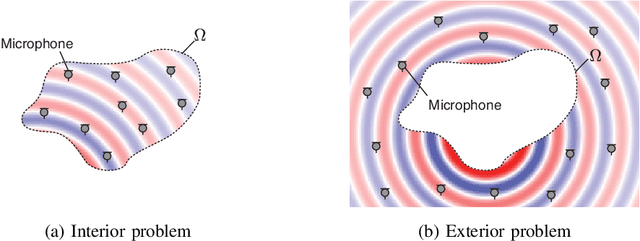
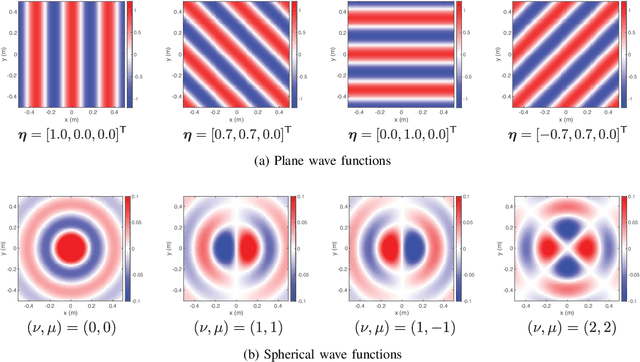
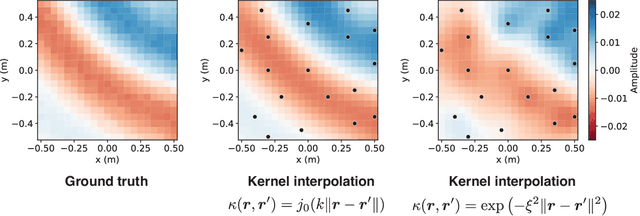
The area of study concerning the estimation of spatial sound, i.e., the distribution of a physical quantity of sound such as acoustic pressure, is called sound field estimation, which is the basis for various applied technologies related to spatial audio processing. The sound field estimation problem is formulated as a function interpolation problem in machine learning in a simplified scenario. However, high estimation performance cannot be expected by simply applying general interpolation techniques that rely only on data. The physical properties of sound fields are useful a priori information, and it is considered extremely important to incorporate them into the estimation. In this article, we introduce the fundamentals of physics-informed machine learning (PIML) for sound field estimation and overview current PIML-based sound field estimation methods.

Kernel Interpolation of Incident Sound Field in Region Including Scattering Objects

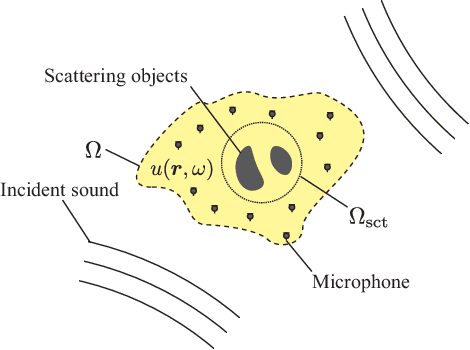
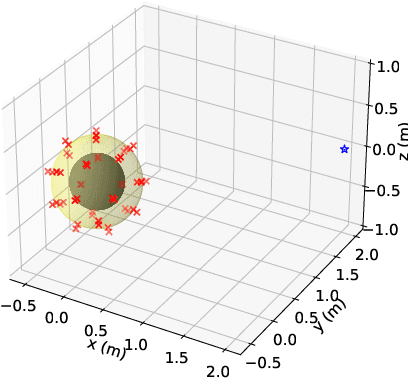
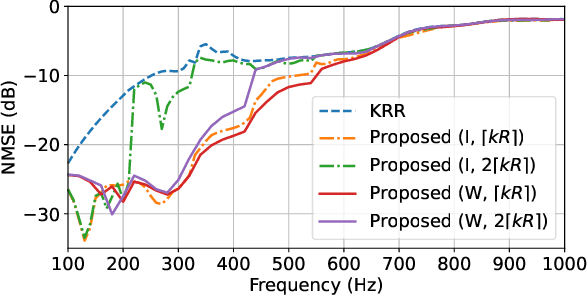
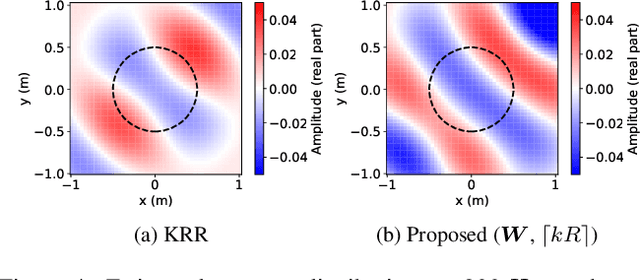
A method for estimating the incident sound field inside a region containing scattering objects is proposed. The sound field estimation method has various applications, such as spatial audio capturing and spatial active noise control; however, most existing methods do not take into account the presence of scatterers within the target estimation region. Although several techniques exist that employ knowledge or measurements of the properties of the scattering objects, it is usually difficult to obtain them precisely in advance, and their properties may change during the estimation process. Our proposed method is based on the kernel ridge regression of the incident field, with a separation from the scattering field represented by a spherical wave function expansion, thus eliminating the need for prior modeling or measurements of the scatterers. Moreover, we introduce a weighting matrix to induce smoothness of the scattering field in the angular direction, which alleviates the effect of the truncation order of the expansion coefficients on the estimation accuracy. Experimental results indicate that the proposed method achieves a higher level of estimation accuracy than the kernel ridge regression without separation.

Kernel interpolation of acoustic transfer functions with adaptive kernel for directed and residual reverberations

An interpolation method for region-to-region acoustic transfer functions (ATFs) based on kernel ridge regression with an adaptive kernel is proposed. Most current ATF interpolation methods do not incorporate the acoustic properties for which measurements are performed. Our proposed method is based on a separate adaptation of directional weighting functions to directed and residual reverberations, which are used for adapting kernel functions. Thus, the proposed method can not only impose constraints on fundamental acoustic properties, but can also adapt to the acoustic environment. Numerical experimental results indicated that our proposed method outperforms the current methods in terms of interpolation accuracy, especially at high frequencies.

Region-to-region kernel interpolation of acoustic transfer function with directional weighting

A method of interpolating the acoustic transfer function (ATF) between regions that takes into account both the physical properties of the ATF and the directionality of region configurations is proposed. Most spatial ATF interpolation methods are limited to estimation in the region of receivers. A kernel method for region-to-region ATF interpolation makes it possible to estimate the ATFs for both source and receiver regions from a discrete set of ATF measurements. We newly formulate the reproducing kernel Hilbert space and associated kernel function incorporating directional weight to enhance the interpolation accuracy. We also investigate hyperparameter optimization methods for this kernel function. Numerical experiments indicate that the proposed method outperforms the method without the use of directional weighting.

Kernel Learning For Sound Field Estimation With L1 and L2 Regularizations

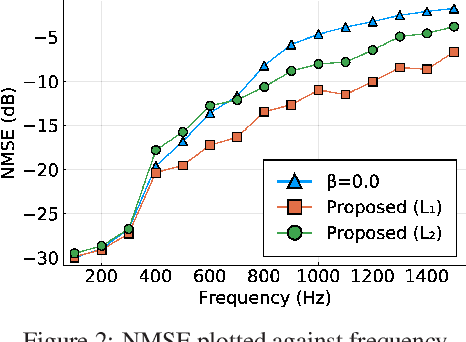
A method to estimate an acoustic field from discrete microphone measurements is proposed. A kernel-interpolation-based method using the kernel function formulated for sound field interpolation has been used in various applications. The kernel function with directional weighting makes it possible to incorporate prior information on source directions to improve estimation accuracy. However, in prior studies, parameters for directional weighting have been empirically determined. We propose a method to optimize these parameters using observation values, which is particularly useful when prior information on source directions is uncertain. The proposed algorithm is based on discretization of the parameters and representation of the kernel function as a weighted sum of sub-kernels. Two types of regularization for the weights, $L_1$ and $L_2$, are investigated. Experimental results indicate that the proposed method achieves higher estimation accuracy than the method without kernel learning.