Low Voltage Electrohydraulic Actuators for Untethered Robotics

Rigid robots can be precise in repetitive tasks but struggle in unstructured environments. Nature's versatility in such environments inspires researchers to develop biomimetic robots that incorporate compliant and contracting artificial muscles. Among the recently proposed artificial muscle technologies, electrohydraulic actuators are promising since they offer comparable performance to mammalian muscles in terms of speed and power density. However, they require high driving voltages and have safety concerns due to exposed electrodes. These high voltages lead to either bulky or inefficient driving electronics that make untethered, high-degree-of-freedom bio-inspired robots difficult to realize. Here, we present low voltage electrohydraulic actuators (LEAs) that match mammalian skeletal muscles in average power density (50.5 W/kg) and peak strain rate (971 percent/s) at a driving voltage of just 1100 V. This driving voltage is approx. 5 - 7 times lower compared to other electrohydraulic actuators using paraelectric dielectrics. Furthermore, LEAs are safe to touch, waterproof, and self-clearing, which makes them easy to implement in wearables and robotics. We characterize, model, and physically validate key performance metrics of the actuator and compare its performance to state-of-the-art electrohydraulic designs. Finally, we demonstrate the utility of our actuators on two muscle-based electrohydraulic robots: an untethered soft robotic swimmer and a robotic gripper. We foresee that LEAs can become a key building block for future highly-biomimetic untethered robots and wearables with many independent artificial muscles such as biomimetic hands, faces, or exoskeletons.

Aquarium: A Fully Differentiable Fluid-Structure Interaction Solver for Robotics Applications

We present Aquarium, a differentiable fluid-structure interaction solver for robotics that offers stable simulation, accurate coupled robot-fluid physics, and full differentiability with respect to fluid states, robot states, and shape parameters. Aquarium achieves stable simulation with accurate flow physics by integrating over the discrete, incompressible Navier-Stokes equations directly using a fully-implicit Crank-Nicolson scheme with a second-order finite-volume spatial discretization. The robot and fluid physics are coupled using the immersed boundary method by formulating the no-slip condition as an equality constraint applied directly to the Navier-Stokes system. This choice of coupling allows the fluid-structure interaction to be posed and solved as a nonlinear optimization problem. This optimization-based formulation is then exploited using the implicit-function theorem to compute derivatives. The derivatives can then be passed to a gradient-based optimization or learning framework. We demonstrate Aquarium's ability to accurately simulate coupled fluid-solid physics with numerous examples, including a cylinder in free stream and a soft robotic tail with hardware validation. We also demonstrate Aquarium's ability to provide full, analytical gradients by performing both shape and gait optimization of a robotic fish tail to maximize generated thrust.

Planar Modeling and Sim-to-Real of a Tethered Multimaterial Soft Swimmer Driven by Peano-HASELs

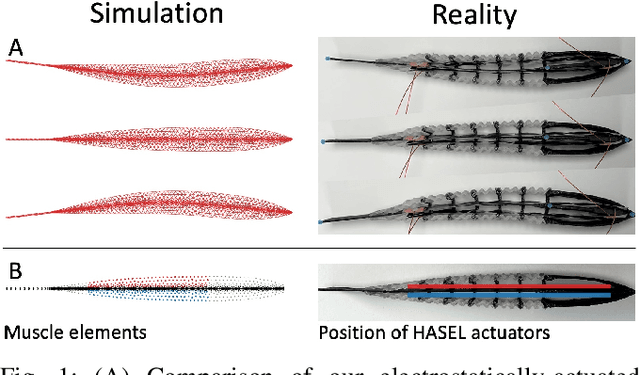
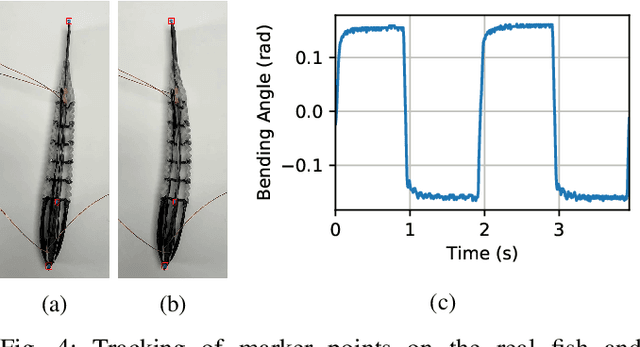
Soft robotics has the potential to revolutionize robotic locomotion, in particular, soft robotic swimmers offer a minimally invasive and adaptive solution to explore and preserve our oceans. Unfortunately, current soft robotic swimmers are vastly inferior to evolved biological swimmers, especially in terms of controllability, efficiency, maneuverability, and longevity. Additionally, the tedious iterative fabrication and empirical testing required to design soft robots has hindered their optimization. In this work, we tackle this challenge by providing an efficient and straightforward pipeline for designing and fabricating soft robotic swimmers equipped with electrostatic actuation. We streamline the process to allow for rapid additive manufacturing, and show how a differentiable simulation can be used to match a simplified model to the real deformation of a robotic swimmer. We perform several experiments with the fabricated swimmer by varying the voltage and actuation frequency of the swimmer's antagonistic muscles. We show how the voltage and frequency vary the locomotion speed of the swimmer while moving in liquid oil and observe a clear optimum in forward swimming speed. The differentiable simulation model we propose has various downstream applications, such as control and shape optimization of the swimmer; optimization results can be directly mapped back to the real robot through our sim-to-real matching.

Physics-constrained Unsupervised Learning of Partial Differential Equations using Meshes

Enhancing neural networks with knowledge of physical equations has become an efficient way of solving various physics problems, from fluid flow to electromagnetism. Graph neural networks show promise in accurately representing irregularly meshed objects and learning their dynamics, but have so far required supervision through large datasets. In this work, we represent meshes naturally as graphs, process these using Graph Networks, and formulate our physics-based loss to provide an unsupervised learning framework for partial differential equations (PDE). We quantitatively compare our results to a classical numerical PDE solver, and show that our computationally efficient approach can be used as an interactive PDE solver that is adjusting boundary conditions in real-time and remains sufficiently close to the baseline solution. Our inherently differentiable framework will enable the application of PDE solvers in interactive settings, such as model-based control of soft-body deformations, or in gradient-based optimization methods that require a fully differentiable pipeline.