Scalable Kernel Logistic Regression with Nyström Approximation: Theoretical Analysis and Application to Discrete Choice Modelling

The application of kernel-based Machine Learning (ML) techniques to discrete choice modelling using large datasets often faces challenges due to memory requirements and the considerable number of parameters involved in these models. This complexity hampers the efficient training of large-scale models. This paper addresses these problems of scalability by introducing the Nystr\"om approximation for Kernel Logistic Regression (KLR) on large datasets. The study begins by presenting a theoretical analysis in which: i) the set of KLR solutions is characterised, ii) an upper bound to the solution of KLR with Nystr\"om approximation is provided, and finally iii) a specialisation of the optimisation algorithms to Nystr\"om KLR is described. After this, the Nystr\"om KLR is computationally validated. Four landmark selection methods are tested, including basic uniform sampling, a k-means sampling strategy, and two non-uniform methods grounded in leverage scores. The performance of these strategies is evaluated using large-scale transport mode choice datasets and is compared with traditional methods such as Multinomial Logit (MNL) and contemporary ML techniques. The study also assesses the efficiency of various optimisation techniques for the proposed Nystr\"om KLR model. The performance of gradient descent, Momentum, Adam, and L-BFGS-B optimisation methods is examined on these datasets. Among these strategies, the k-means Nystr\"om KLR approach emerges as a successful solution for applying KLR to large datasets, particularly when combined with the L-BFGS-B and Adam optimisation methods. The results highlight the ability of this strategy to handle datasets exceeding 200,000 observations while maintaining robust performance.

ciDATGAN: Conditional Inputs for Tabular GANs

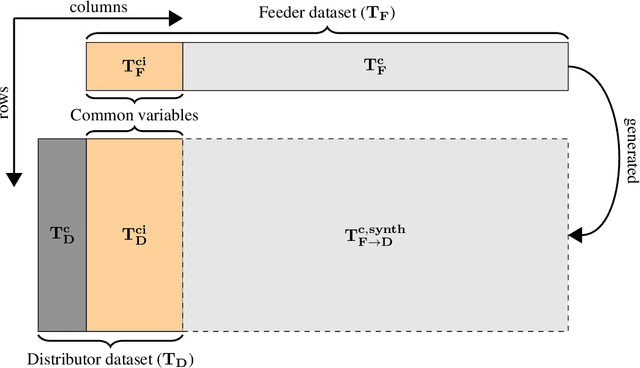
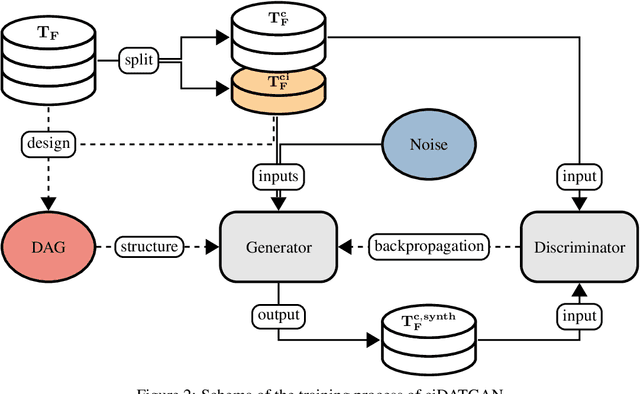
Conditionality has become a core component for Generative Adversarial Networks (GANs) for generating synthetic images. GANs are usually using latent conditionality to control the generation process. However, tabular data only contains manifest variables. Thus, latent conditionality either restricts the generated data or does not produce sufficiently good results. Therefore, we propose a new methodology to include conditionality in tabular GANs inspired by image completion methods. This article presents ciDATGAN, an evolution of the Directed Acyclic Tabular GAN (DATGAN) that has already been shown to outperform state-of-the-art tabular GAN models. First, we show that the addition of conditional inputs does hinder the model's performance compared to its predecessor. Then, we demonstrate that ciDATGAN can be used to unbias datasets with the help of well-chosen conditional inputs. Finally, it shows that ciDATGAN can learn the logic behind the data and, thus, be used to complete large synthetic datasets using data from a smaller feeder dataset.

DATGAN: Integrating expert knowledge into deep learning for synthetic tabular data

Synthetic data can be used in various applications, such as correcting bias datasets or replacing scarce original data for simulation purposes. Generative Adversarial Networks (GANs) are considered state-of-the-art for developing generative models. However, these deep learning models are data-driven, and it is, thus, difficult to control the generation process. It can, therefore, lead to the following issues: lack of representativity in the generated data, the introduction of bias, and the possibility of overfitting the sample's noise. This article presents the Directed Acyclic Tabular GAN (DATGAN) to address these limitations by integrating expert knowledge in deep learning models for synthetic tabular data generation. This approach allows the interactions between variables to be specified explicitly using a Directed Acyclic Graph (DAG). The DAG is then converted to a network of modified Long Short-Term Memory (LSTM) cells to accept multiple inputs. Multiple DATGAN versions are systematically tested on multiple assessment metrics. We show that the best versions of the DATGAN outperform state-of-the-art generative models on multiple case studies. Finally, we show how the DAG can create hypothetical synthetic datasets.

Bayesian Automatic Relevance Determination for Utility Function Specification in Discrete Choice Models

Specifying utility functions is a key step towards applying the discrete choice framework for understanding the behaviour processes that govern user choices. However, identifying the utility function specifications that best model and explain the observed choices can be a very challenging and time-consuming task. This paper seeks to help modellers by leveraging the Bayesian framework and the concept of automatic relevance determination (ARD), in order to automatically determine an optimal utility function specification from an exponentially large set of possible specifications in a purely data-driven manner. Based on recent advances in approximate Bayesian inference, a doubly stochastic variational inference is developed, which allows the proposed DCM-ARD model to scale to very large and high-dimensional datasets. Using semi-artificial choice data, the proposed approach is shown to very accurately recover the true utility function specifications that govern the observed choices. Moreover, when applied to real choice data, DCM-ARD is shown to be able discover high quality specifications that can outperform previous ones from the literature according to multiple criteria, thereby demonstrating its practical applicability.

Pólygamma Data Augmentation to address Non-conjugacy in the Bayesian Estimation of Mixed Multinomial Logit Models

The standard Gibbs sampler of Mixed Multinomial Logit (MMNL) models involves sampling from conditional densities of utility parameters using Metropolis-Hastings (MH) algorithm due to unavailability of conjugate prior for logit kernel. To address this non-conjugacy concern, we propose the application of P\'olygamma data augmentation (PG-DA) technique for the MMNL estimation. The posterior estimates of the augmented and the default Gibbs sampler are similar for two-alternative scenario (binary choice), but we encounter empirical identification issues in the case of more alternatives ($J \geq 3$).

Bayesian Estimation of Mixed Multinomial Logit Models: Advances and Simulation-Based Evaluations

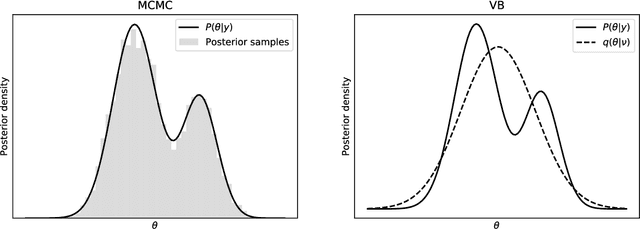
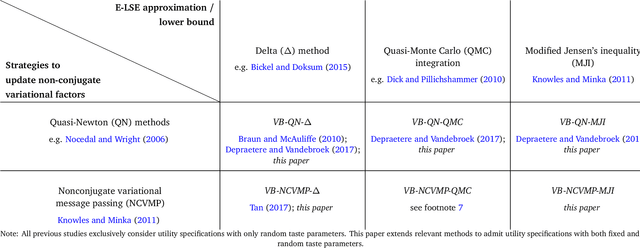
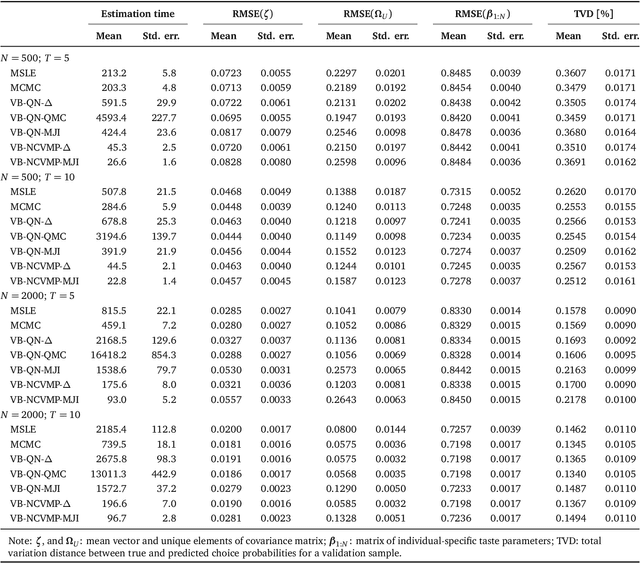
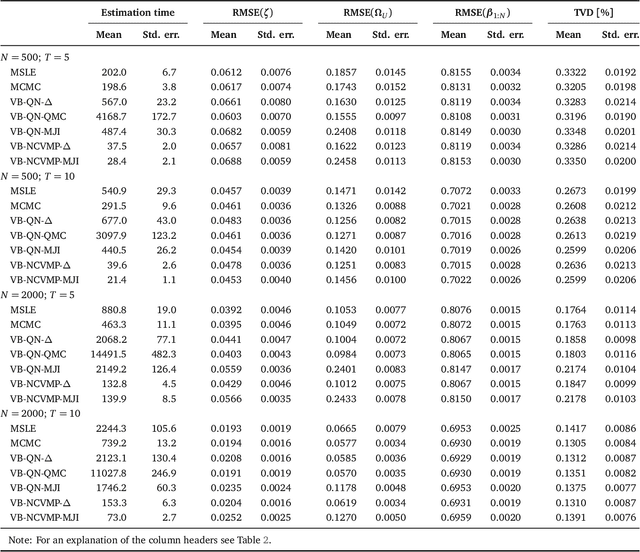
Variational Bayes (VB) methods have emerged as a fast and computationally-efficient alternative to Markov chain Monte Carlo (MCMC) methods for Bayesian estimation of mixed multinomial logit (MMNL) models. It has been established that VB is substantially faster than MCMC at practically no compromises in predictive accuracy. In this paper, we address two critical gaps concerning the usage and understanding of VB for MMNL. First, extant VB methods are limited to utility specifications involving only individual-specific taste parameters. Second, the finite-sample properties of VB estimators and the relative performance of VB, MCMC and maximum simulated likelihood estimation (MSLE) are not known. To address the former, this study extends several VB methods for MMNL to admit utility specifications including both fixed and random utility parameters. To address the latter, we conduct an extensive simulation-based evaluation to benchmark the extended VB methods against MCMC and MSLE in terms of estimation times, parameter recovery and predictive accuracy. The results suggest that all VB variants perform as well as MCMC and MSLE at prediction and recovery of all model parameters with the exception of the covariance matrix of the multivariate normal mixing distribution. In particular, VB with nonconjugate variational message passing and the delta-method (VB-NCVMP-Delta) is relatively accurate and up to 15 times faster than MCMC and MSLE. On the whole, VB-NCVMP-Delta is most suitable for applications in which fast predictions are paramount, while MCMC should be preferred in applications in which accurate inferences are most important.