Bayesian Deep Learning for Discrete Choice

Discrete choice models (DCMs) are used to analyze individual decision-making in contexts such as transportation choices, political elections, and consumer preferences. DCMs play a central role in applied econometrics by enabling inference on key economic variables, such as marginal rates of substitution, rather than focusing solely on predicting choices on new unlabeled data. However, while traditional DCMs offer high interpretability and support for point and interval estimation of economic quantities, these models often underperform in predictive tasks compared to deep learning (DL) models. Despite their predictive advantages, DL models remain largely underutilized in discrete choice due to concerns about their lack of interpretability, unstable parameter estimates, and the absence of established methods for uncertainty quantification. Here, we introduce a deep learning model architecture specifically designed to integrate with approximate Bayesian inference methods, such as Stochastic Gradient Langevin Dynamics (SGLD). Our proposed model collapses to behaviorally informed hypotheses when data is limited, mitigating overfitting and instability in underspecified settings while retaining the flexibility to capture complex nonlinear relationships when sufficient data is available. We demonstrate our approach using SGLD through a Monte Carlo simulation study, evaluating both predictive metrics--such as out-of-sample balanced accuracy--and inferential metrics--such as empirical coverage for marginal rates of substitution interval estimates. Additionally, we present results from two empirical case studies: one using revealed mode choice data in NYC, and the other based on the widely used Swiss train choice stated preference data.

Designing Graph Convolutional Neural Networks for Discrete Choice with Network Effects

We introduce a novel model architecture that incorporates network effects into discrete choice problems, achieving higher predictive performance than standard discrete choice models while offering greater interpretability than general-purpose flexible model classes. Econometric discrete choice models aid in studying individual decision-making, where agents select the option with the highest reward from a discrete set of alternatives. Intuitively, the utility an individual derives from a particular choice depends on their personal preferences and characteristics, the attributes of the alternative, and the value their peers assign to that alternative or their previous choices. However, most applications ignore peer influence, and models that do consider peer or network effects often lack the flexibility and predictive performance of recently developed approaches to discrete choice, such as deep learning. We propose a novel graph convolutional neural network architecture to model network effects in discrete choices, achieving higher predictive performance than standard discrete choice models while retaining the interpretability necessary for inference--a quality often lacking in general-purpose deep learning architectures. We evaluate our architecture using revealed commuting choice data, extended with travel times and trip costs for each travel mode for work-related trips in New York City, as well as 2016 U.S. election data aggregated by county, to test its performance on datasets with highly imbalanced classes. Given the interpretability of our models, we can estimate relevant economic metrics, such as the value of travel time savings in New York City. Finally, we compare the predictive performance and behavioral insights from our architecture to those derived from traditional discrete choice and general-purpose deep learning models.

Pólygamma Data Augmentation to address Non-conjugacy in the Bayesian Estimation of Mixed Multinomial Logit Models

The standard Gibbs sampler of Mixed Multinomial Logit (MMNL) models involves sampling from conditional densities of utility parameters using Metropolis-Hastings (MH) algorithm due to unavailability of conjugate prior for logit kernel. To address this non-conjugacy concern, we propose the application of P\'olygamma data augmentation (PG-DA) technique for the MMNL estimation. The posterior estimates of the augmented and the default Gibbs sampler are similar for two-alternative scenario (binary choice), but we encounter empirical identification issues in the case of more alternatives ($J \geq 3$).

Bayesian Estimation of Mixed Multinomial Logit Models: Advances and Simulation-Based Evaluations

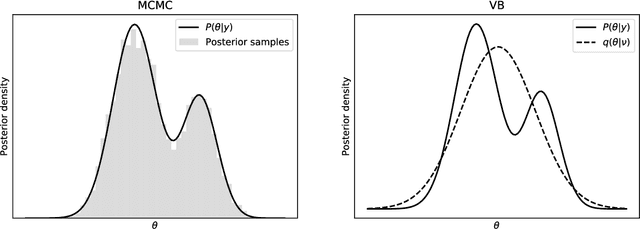
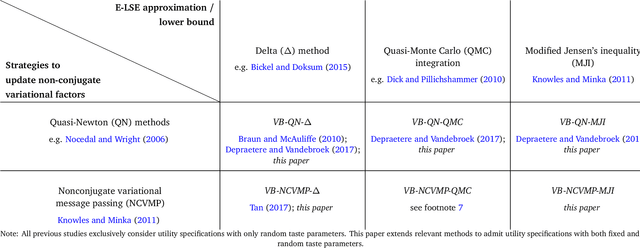
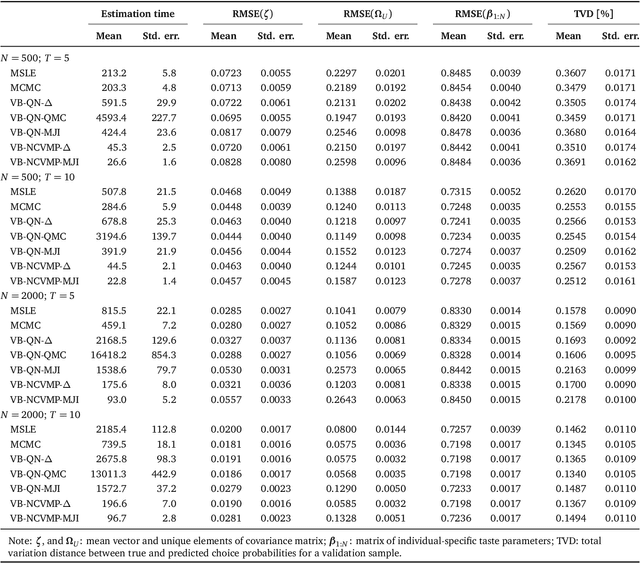
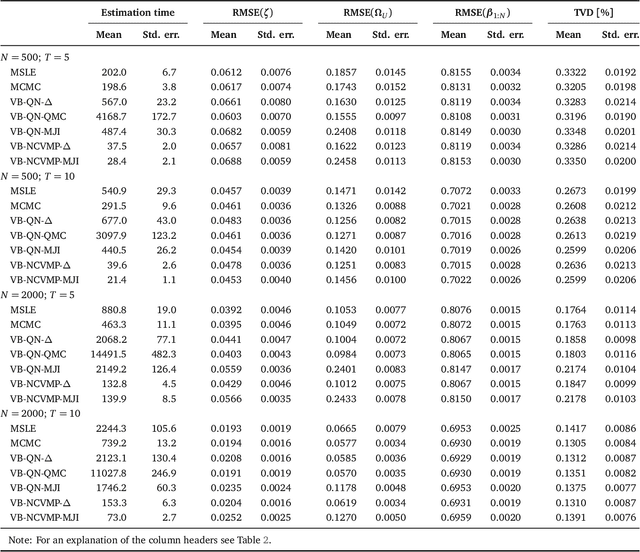
Variational Bayes (VB) methods have emerged as a fast and computationally-efficient alternative to Markov chain Monte Carlo (MCMC) methods for Bayesian estimation of mixed multinomial logit (MMNL) models. It has been established that VB is substantially faster than MCMC at practically no compromises in predictive accuracy. In this paper, we address two critical gaps concerning the usage and understanding of VB for MMNL. First, extant VB methods are limited to utility specifications involving only individual-specific taste parameters. Second, the finite-sample properties of VB estimators and the relative performance of VB, MCMC and maximum simulated likelihood estimation (MSLE) are not known. To address the former, this study extends several VB methods for MMNL to admit utility specifications including both fixed and random utility parameters. To address the latter, we conduct an extensive simulation-based evaluation to benchmark the extended VB methods against MCMC and MSLE in terms of estimation times, parameter recovery and predictive accuracy. The results suggest that all VB variants perform as well as MCMC and MSLE at prediction and recovery of all model parameters with the exception of the covariance matrix of the multivariate normal mixing distribution. In particular, VB with nonconjugate variational message passing and the delta-method (VB-NCVMP-Delta) is relatively accurate and up to 15 times faster than MCMC and MSLE. On the whole, VB-NCVMP-Delta is most suitable for applications in which fast predictions are paramount, while MCMC should be preferred in applications in which accurate inferences are most important.