Fast Bayesian Estimation of Spatial Count Data Models

Spatial count data models are used to explain and predict the frequency of phenomena such as traffic accidents in geographically distinct entities such as census tracts or road segments. These models are typically estimated using Bayesian Markov chain Monte Carlo (MCMC) simulation methods, which, however, are computationally expensive and do not scale well to large datasets. Variational Bayes (VB), a method from machine learning, addresses the shortcomings of MCMC by casting Bayesian estimation as an optimisation problem instead of a simulation problem. In this paper, we derive a VB method for posterior inference in negative binomial models with unobserved parameter heterogeneity and spatial dependence. The proposed method uses Polya-Gamma augmentation to deal with the non-conjugacy of the negative binomial likelihood and an integrated non-factorised specification of the variational distribution to capture posterior dependencies. We demonstrate the benefits of the approach using simulated data and real data on youth pedestrian injury counts in the census tracts of New York City boroughs Bronx and Manhattan. The empirical analysis suggests that the VB approach is between 7 and 13 times faster than MCMC on a regular eight-core processor, while offering similar estimation and predictive accuracy. Conditional on the availability of computational resources, the embarrassingly parallel architecture of the proposed VB method can be exploited to further accelerate the estimation by up to 100 times.

Pólygamma Data Augmentation to address Non-conjugacy in the Bayesian Estimation of Mixed Multinomial Logit Models

The standard Gibbs sampler of Mixed Multinomial Logit (MMNL) models involves sampling from conditional densities of utility parameters using Metropolis-Hastings (MH) algorithm due to unavailability of conjugate prior for logit kernel. To address this non-conjugacy concern, we propose the application of P\'olygamma data augmentation (PG-DA) technique for the MMNL estimation. The posterior estimates of the augmented and the default Gibbs sampler are similar for two-alternative scenario (binary choice), but we encounter empirical identification issues in the case of more alternatives ($J \geq 3$).

Bayesian Estimation of Mixed Multinomial Logit Models: Advances and Simulation-Based Evaluations

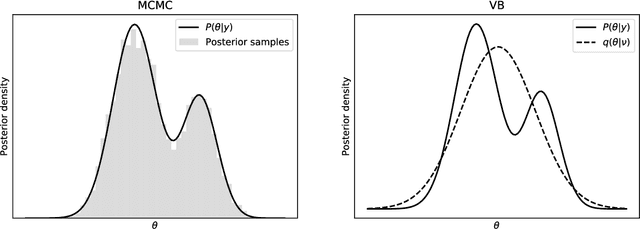
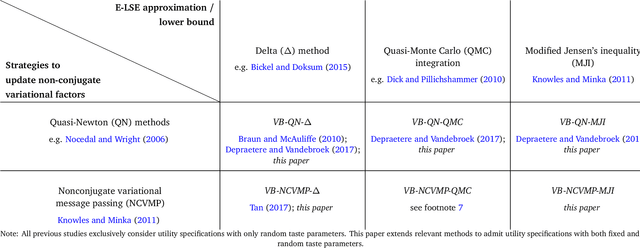
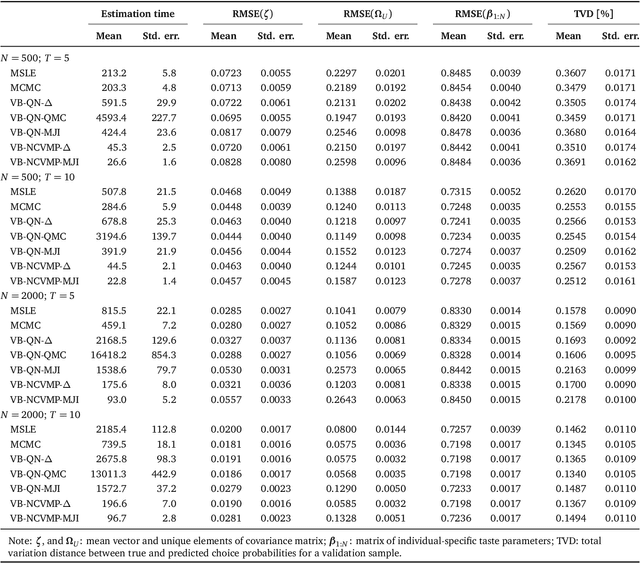
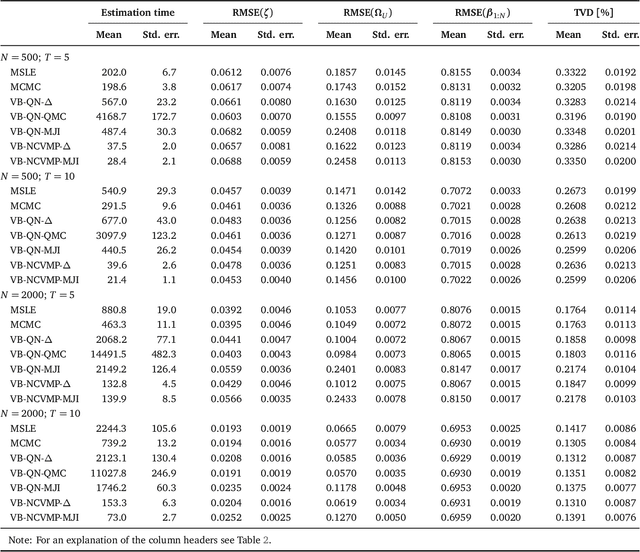
Variational Bayes (VB) methods have emerged as a fast and computationally-efficient alternative to Markov chain Monte Carlo (MCMC) methods for Bayesian estimation of mixed multinomial logit (MMNL) models. It has been established that VB is substantially faster than MCMC at practically no compromises in predictive accuracy. In this paper, we address two critical gaps concerning the usage and understanding of VB for MMNL. First, extant VB methods are limited to utility specifications involving only individual-specific taste parameters. Second, the finite-sample properties of VB estimators and the relative performance of VB, MCMC and maximum simulated likelihood estimation (MSLE) are not known. To address the former, this study extends several VB methods for MMNL to admit utility specifications including both fixed and random utility parameters. To address the latter, we conduct an extensive simulation-based evaluation to benchmark the extended VB methods against MCMC and MSLE in terms of estimation times, parameter recovery and predictive accuracy. The results suggest that all VB variants perform as well as MCMC and MSLE at prediction and recovery of all model parameters with the exception of the covariance matrix of the multivariate normal mixing distribution. In particular, VB with nonconjugate variational message passing and the delta-method (VB-NCVMP-Delta) is relatively accurate and up to 15 times faster than MCMC and MSLE. On the whole, VB-NCVMP-Delta is most suitable for applications in which fast predictions are paramount, while MCMC should be preferred in applications in which accurate inferences are most important.

A Dirichlet Process Mixture Model of Discrete Choice

We present a mixed multinomial logit (MNL) model, which leverages the truncated stick-breaking process representation of the Dirichlet process as a flexible nonparametric mixing distribution. The proposed model is a Dirichlet process mixture model and accommodates discrete representations of heterogeneity, like a latent class MNL model. Yet, unlike a latent class MNL model, the proposed discrete choice model does not require the analyst to fix the number of mixture components prior to estimation, as the complexity of the discrete mixing distribution is inferred from the evidence. For posterior inference in the proposed Dirichlet process mixture model of discrete choice, we derive an expectation maximisation algorithm. In a simulation study, we demonstrate that the proposed model framework can flexibly capture differently-shaped taste parameter distributions. Furthermore, we empirically validate the model framework in a case study on motorists' route choice preferences and find that the proposed Dirichlet process mixture model of discrete choice outperforms a latent class MNL model and mixed MNL models with common parametric mixing distributions in terms of both in-sample fit and out-of-sample predictive ability. Compared to extant modelling approaches, the proposed discrete choice model substantially abbreviates specification searches, as it relies on less restrictive parametric assumptions and does not require the analyst to specify the complexity of the discrete mixing distribution prior to estimation.