Compact: Approximating Complex Activation Functions for Secure Computation

Secure multi-party computation (MPC) techniques can be used to provide data privacy when users query deep neural network (DNN) models hosted on a public cloud. State-of-the-art MPC techniques can be directly leveraged for DNN models that use simple activation functions (AFs) such as ReLU. However, DNN model architectures designed for cutting-edge applications often use complex and highly non-linear AFs. Designing efficient MPC techniques for such complex AFs is an open problem. Towards this, we propose Compact, which produces piece-wise polynomial approximations of complex AFs to enable their efficient use with state-of-the-art MPC techniques. Compact neither requires nor imposes any restriction on model training and results in near-identical model accuracy. We extensively evaluate Compact on four different machine-learning tasks with DNN architectures that use popular complex AFs SiLU, GeLU, and Mish. Our experimental results show that Compact incurs negligible accuracy loss compared to DNN-specific approaches for handling complex non-linear AFs. We also incorporate Compact in two state-of-the-art MPC libraries for privacy-preserving inference and demonstrate that Compact provides 2x-5x speedup in computation compared to the state-of-the-art approximation approach for non-linear functions -- while providing similar or better accuracy for DNN models with large number of hidden layers

Deconvolutional Density Network: Free-Form Conditional Density Estimation

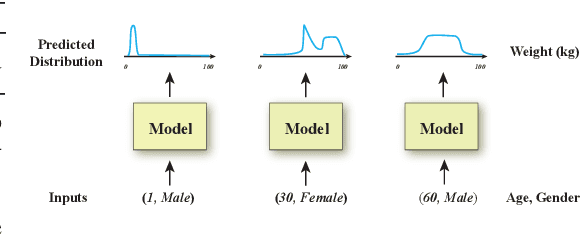
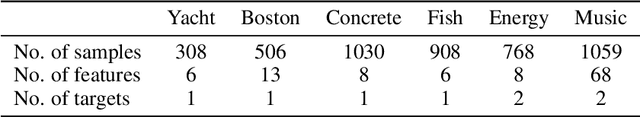
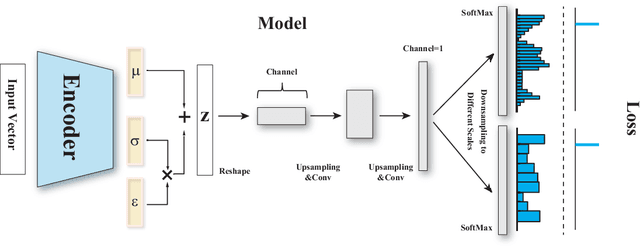
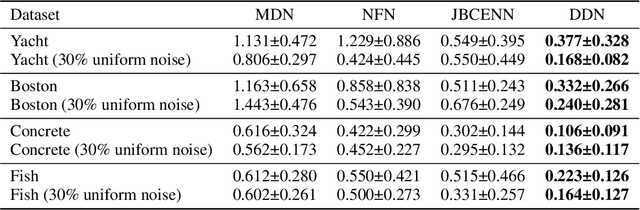
Conditional density estimation is the task of estimating the probability of an event, conditioned on some inputs. A neural network can be used to compute the output distribution explicitly. For such a task, there are many ways to represent a continuous-domain distribution using the output of a neural network, but each comes with its own limitations for what distributions it can accurately render. If the family of functions is too restrictive, it will not be appropriate for many datasets. In this paper, we demonstrate the benefits of modeling free-form distributions using deconvolution. It has the advantage of being flexible, but also takes advantage of the topological smoothness offered by the deconvolution layers. We compare our method to a number of other density-estimation approaches, and show that our Deconvolutional Density Network (DDN) outperforms the competing methods on many artificial and real tasks, without committing to a restrictive parametric model.

Dimensionality Reduction for Sentiment Classification: Evolving for the Most Prominent and Separable Features

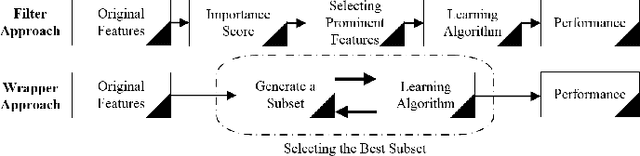
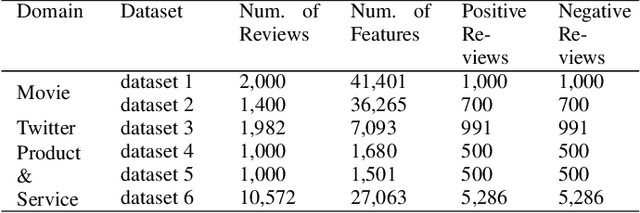
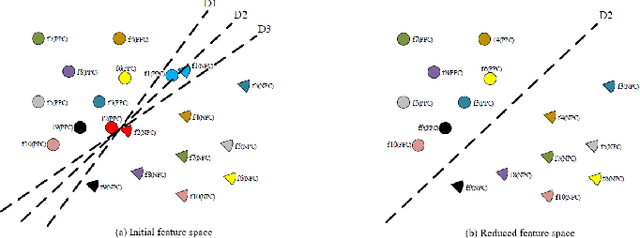
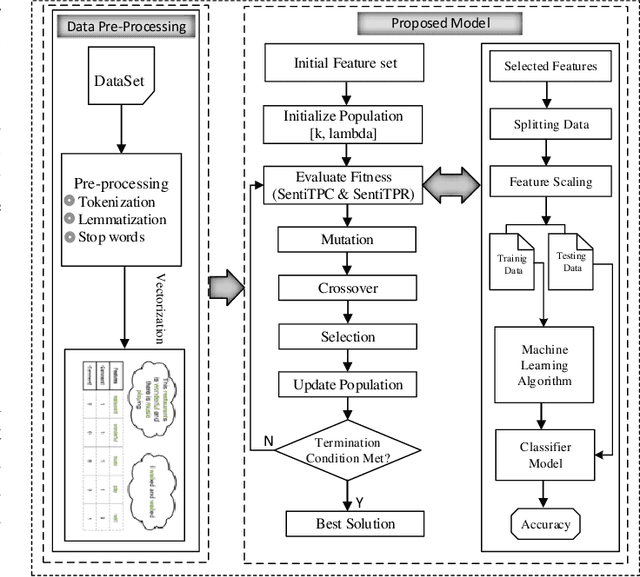
In sentiment classification, the enormous amount of textual data, its immense dimensionality, and inherent noise make it extremely difficult for machine learning classifiers to extract high-level and complex abstractions. In order to make the data less sparse and more statistically significant, the dimensionality reduction techniques are needed. But in the existing dimensionality reduction techniques, the number of components needs to be set manually which results in loss of the most prominent features, thus reducing the performance of the classifiers. Our prior work, i.e., Term Presence Count (TPC) and Term Presence Ratio (TPR) have proven to be effective techniques as they reject the less separable features. However, the most prominent and separable features might still get removed from the initial feature set despite having higher distributions among positive and negative tagged documents. To overcome this problem, we have proposed a new framework that consists of two-dimensionality reduction techniques i.e., Sentiment Term Presence Count (SentiTPC) and Sentiment Term Presence Ratio (SentiTPR). These techniques reject the features by considering term presence difference for SentiTPC and ratio of the distribution distinction for SentiTPR. Additionally, these methods also analyze the total distribution information. Extensive experimental results exhibit that the proposed framework reduces the feature dimension by a large scale, and thus significantly improve the classification performance.

Improving Neural Network Classifier using Gradient-based Floating Centroid Method

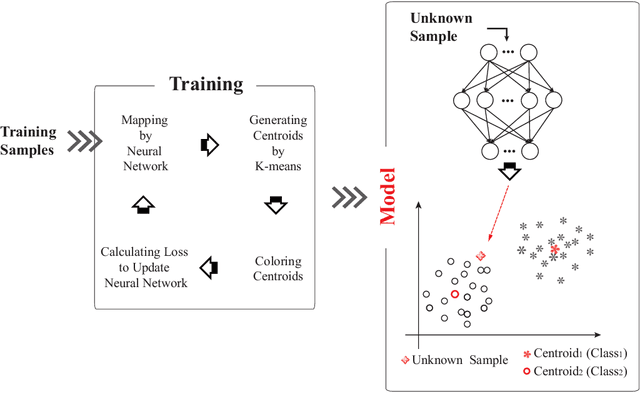
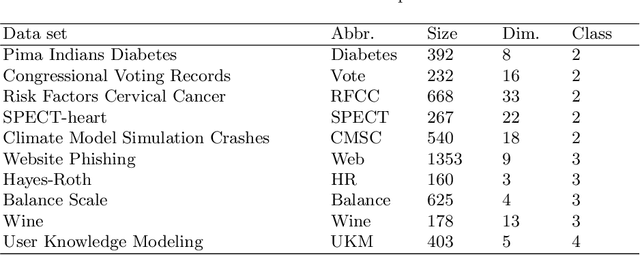
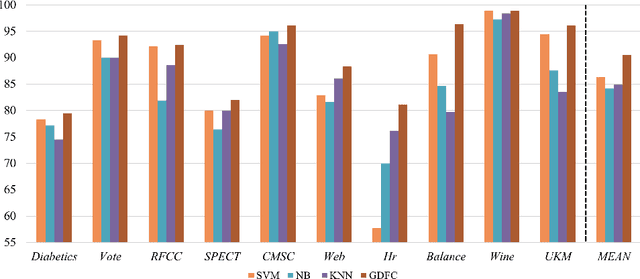
Floating centroid method (FCM) offers an efficient way to solve a fixed-centroid problem for the neural network classifiers. However, evolutionary computation as its optimization method restrains the FCM to achieve satisfactory performance for different neural network structures, because of the high computational complexity and inefficiency. Traditional gradient-based methods have been extensively adopted to optimize the neural network classifiers. In this study, a gradient-based floating centroid (GDFC) method is introduced to address the fixed centroid problem for the neural network classifiers optimized by gradient-based methods. Furthermore, a new loss function for optimizing GDFC is introduced. The experimental results display that GDFC obtains promising classification performance than the comparison methods on the benchmark datasets.