Disentanglement in Difference: Directly Learning Semantically Disentangled Representations by Maximizing Inter-Factor Differences

In this study, Disentanglement in Difference(DiD) is proposed to address the inherent inconsistency between the statistical independence of latent variables and the goal of semantic disentanglement in disentanglement representation learning. Conventional disentanglement methods achieve disentanglement representation by improving statistical independence among latent variables. However, the statistical independence of latent variables does not necessarily imply that they are semantically unrelated, thus, improving statistical independence does not always enhance disentanglement performance. To address the above issue, DiD is proposed to directly learn semantic differences rather than the statistical independence of latent variables. In the DiD, a Difference Encoder is designed to measure the semantic differences; a contrastive loss function is established to facilitate inter-dimensional comparison. Both of them allow the model to directly differentiate and disentangle distinct semantic factors, thereby resolving the inconsistency between statistical independence and semantic disentanglement. Experimental results on the dSprites and 3DShapes datasets demonstrate that the proposed DiD outperforms existing mainstream methods across various disentanglement metrics.

Black-Box Optimization via Generative Adversarial Nets

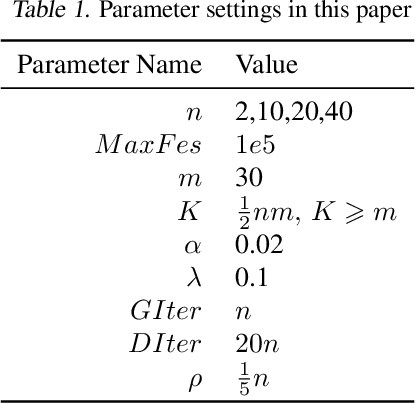
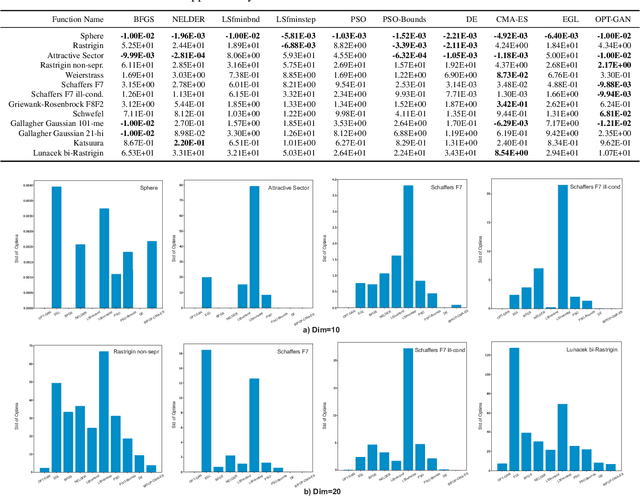
Black-box optimization (BBO) algorithms are concerned with finding the best solutions for the problems with missing analytical details. Most classical methods for such problems are based on strong and fixed \emph{a priori} assumptions such as Gaussian distribution. However, lots of complex real-world problems are far from the \emph{a priori} distribution, bringing some unexpected obstacles to these methods. In this paper, we present an optimizer using generative adversarial nets (OPT-GAN) to guide search on black-box problems via estimating the distribution of optima. The method learns the extensive distribution of the optimal region dominated by selective candidates. Experiments demonstrate that OPT-GAN outperforms other classical BBO algorithms, in particular the ones with Gaussian assumptions.

Improving Neural Network Classifier using Gradient-based Floating Centroid Method

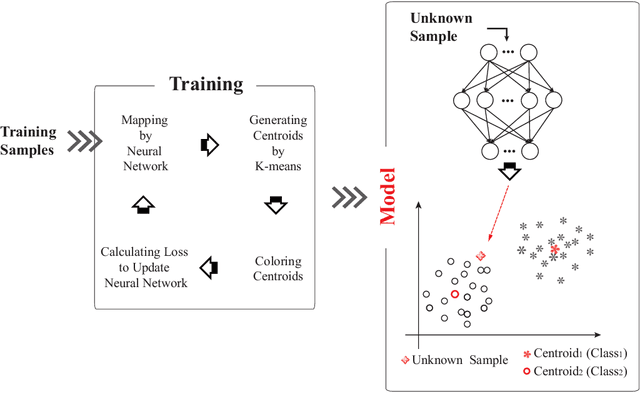
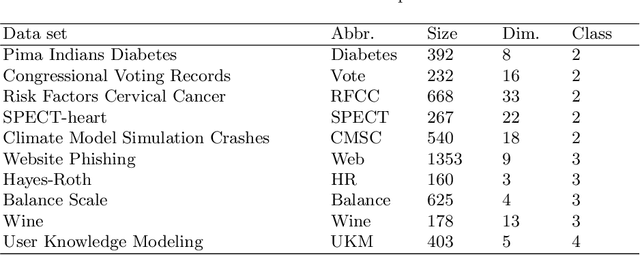
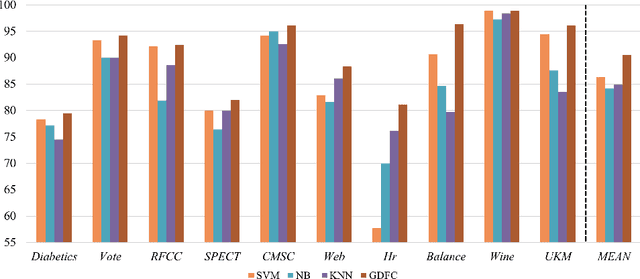
Floating centroid method (FCM) offers an efficient way to solve a fixed-centroid problem for the neural network classifiers. However, evolutionary computation as its optimization method restrains the FCM to achieve satisfactory performance for different neural network structures, because of the high computational complexity and inefficiency. Traditional gradient-based methods have been extensively adopted to optimize the neural network classifiers. In this study, a gradient-based floating centroid (GDFC) method is introduced to address the fixed centroid problem for the neural network classifiers optimized by gradient-based methods. Furthermore, a new loss function for optimizing GDFC is introduced. The experimental results display that GDFC obtains promising classification performance than the comparison methods on the benchmark datasets.