Deconvolutional Density Network: Free-Form Conditional Density Estimation

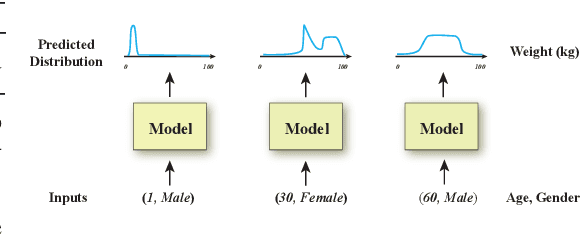
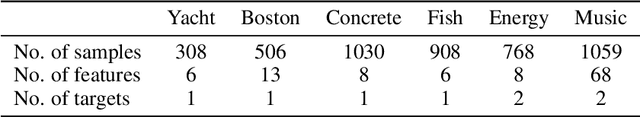
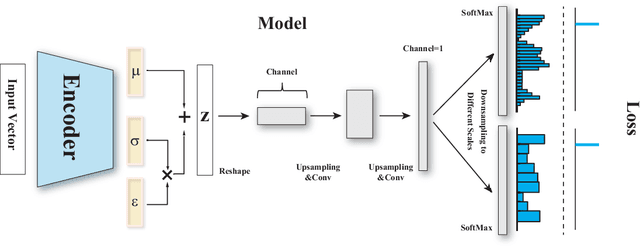
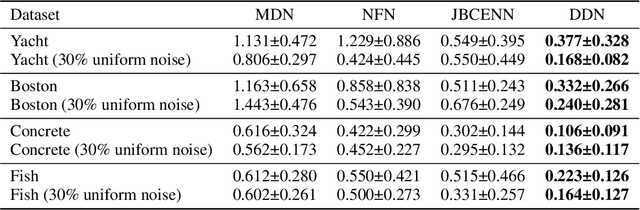
Conditional density estimation is the task of estimating the probability of an event, conditioned on some inputs. A neural network can be used to compute the output distribution explicitly. For such a task, there are many ways to represent a continuous-domain distribution using the output of a neural network, but each comes with its own limitations for what distributions it can accurately render. If the family of functions is too restrictive, it will not be appropriate for many datasets. In this paper, we demonstrate the benefits of modeling free-form distributions using deconvolution. It has the advantage of being flexible, but also takes advantage of the topological smoothness offered by the deconvolution layers. We compare our method to a number of other density-estimation approaches, and show that our Deconvolutional Density Network (DDN) outperforms the competing methods on many artificial and real tasks, without committing to a restrictive parametric model.