Probabilistic inverse optimal control with local linearization for non-linear partially observable systems

Inverse optimal control methods can be used to characterize behavior in sequential decision-making tasks. Most existing work, however, requires the control signals to be known, or is limited to fully-observable or linear systems. This paper introduces a probabilistic approach to inverse optimal control for stochastic non-linear systems with missing control signals and partial observability that unifies existing approaches. By using an explicit model of the noise characteristics of the sensory and control systems of the agent in conjunction with local linearization techniques, we derive an approximate likelihood for the model parameters, which can be computed within a single forward pass. We evaluate our proposed method on stochastic and partially observable version of classic control tasks, a navigation task, and a manual reaching task. The proposed method has broad applicability, ranging from imitation learning to sensorimotor neuroscience.

Reinforcement Learning with Non-Exponential Discounting

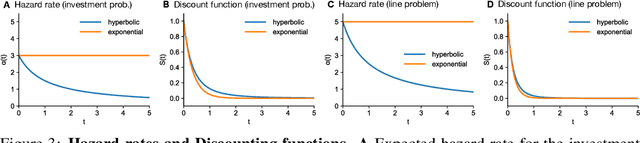
Commonly in reinforcement learning (RL), rewards are discounted over time using an exponential function to model time preference, thereby bounding the expected long-term reward. In contrast, in economics and psychology, it has been shown that humans often adopt a hyperbolic discounting scheme, which is optimal when a specific task termination time distribution is assumed. In this work, we propose a theory for continuous-time model-based reinforcement learning generalized to arbitrary discount functions. This formulation covers the case in which there is a non-exponential random termination time. We derive a Hamilton-Jacobi-Bellman (HJB) equation characterizing the optimal policy and describe how it can be solved using a collocation method, which uses deep learning for function approximation. Further, we show how the inverse RL problem can be approached, in which one tries to recover properties of the discount function given decision data. We validate the applicability of our proposed approach on two simulated problems. Our approach opens the way for the analysis of human discounting in sequential decision-making tasks.

Inverse Optimal Control Adapted to the Noise Characteristics of the Human Sensorimotor System

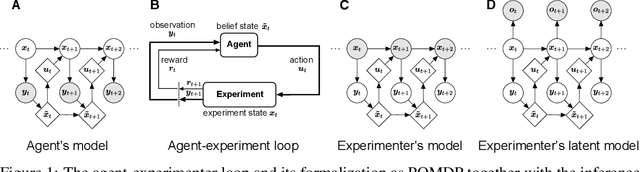
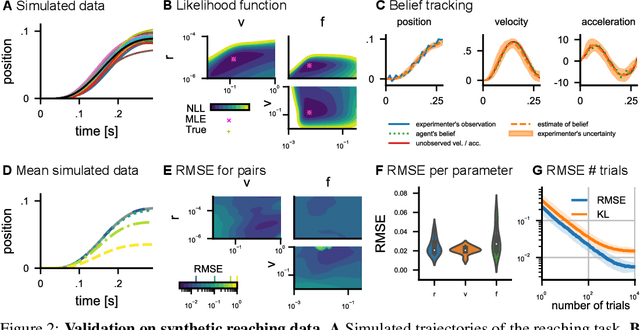
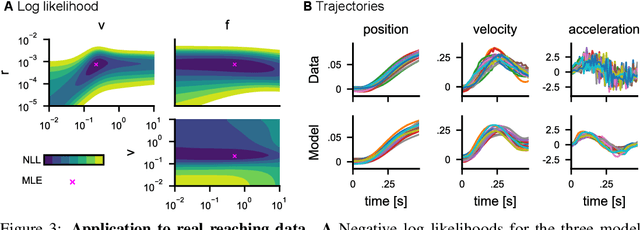
Computational level explanations based on optimal feedback control with signal-dependent noise have been able to account for a vast array of phenomena in human sensorimotor behavior. However, commonly a cost function needs to be assumed for a task and the optimality of human behavior is evaluated by comparing observed and predicted trajectories. Here, we introduce inverse optimal control with signal-dependent noise, which allows inferring the cost function from observed behavior. To do so, we formalize the problem as a partially observable Markov decision process and distinguish between the agent's and the experimenter's inference problems. Specifically, we derive a probabilistic formulation of the evolution of states and belief states and an approximation to the propagation equation in the linear-quadratic Gaussian problem with signal-dependent noise. We extend the model to the case of partial observability of state variables from the point of view of the experimenter. We show the feasibility of the approach through validation on synthetic data and application to experimental data. Our approach enables recovering the costs and benefits implicit in human sequential sensorimotor behavior, thereby reconciling normative and descriptive approaches in a computational framework.

POMDPs in Continuous Time and Discrete Spaces

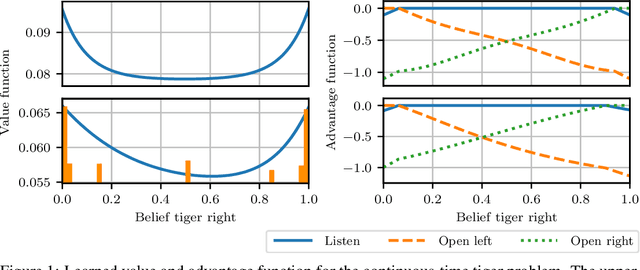
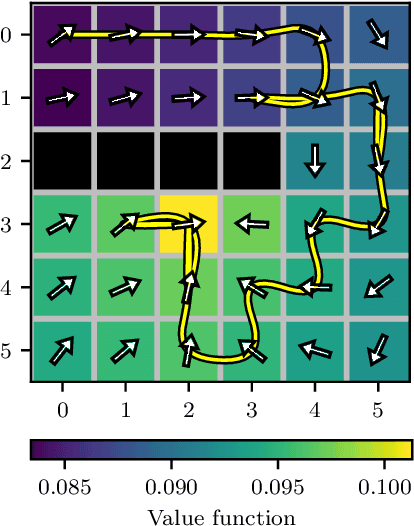
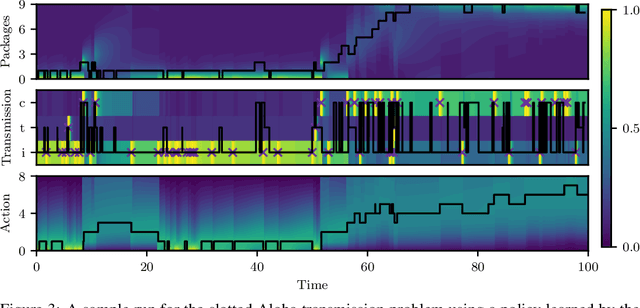
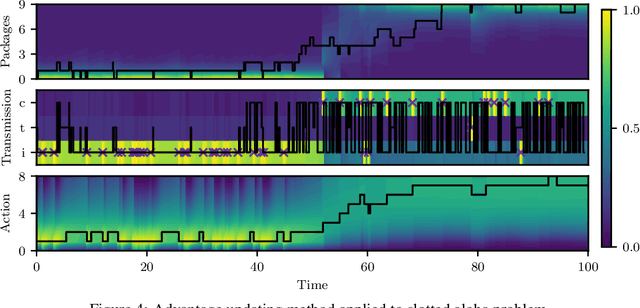
Many processes, such as discrete event systems in engineering or population dynamics in biology, evolve in discrete space and continuous time. We consider the problem of optimal decision making in such discrete state and action space systems under partial observability. This places our work at the intersection of optimal filtering and optimal control. At the current state of research, a mathematical description for simultaneous decision making and filtering in continuous time with finite state and action spaces is still missing. In this paper, we give a mathematical description of a continuous-time partial observable Markov decision process (POMDP). By leveraging optimal filtering theory we derive a Hamilton-Jacobi-Bellman (HJB) type equation that characterizes the optimal solution. Using techniques from deep learning we approximately solve the resulting partial integro-differential equation. We present (i) an approach solving the decision problem offline by learning an approximation of the value function and (ii) an online algorithm which provides a solution in belief space using deep reinforcement learning. We show the applicability on a set of toy examples which pave the way for future methods providing solutions for high dimensional problems.

Receding Horizon Curiosity

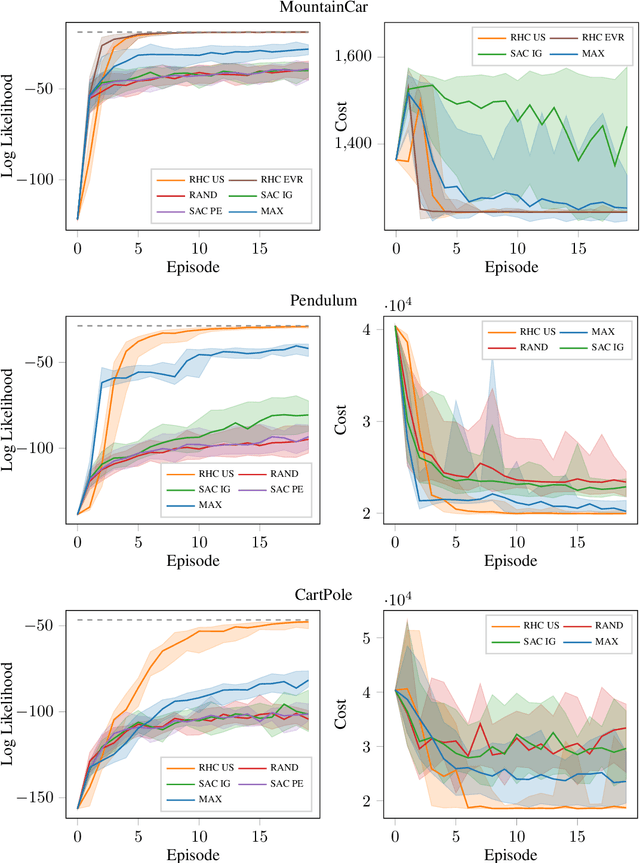
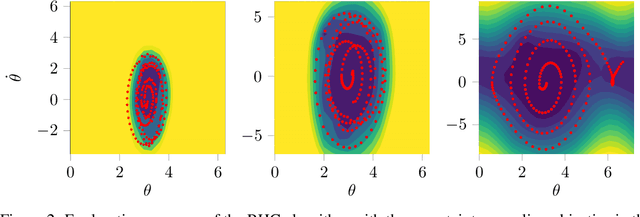
Sample-efficient exploration is crucial not only for discovering rewarding experiences but also for adapting to environment changes in a task-agnostic fashion. A principled treatment of the problem of optimal input synthesis for system identification is provided within the framework of sequential Bayesian experimental design. In this paper, we present an effective trajectory-optimization-based approximate solution of this otherwise intractable problem that models optimal exploration in an unknown Markov decision process (MDP). By interleaving episodic exploration with Bayesian nonlinear system identification, our algorithm takes advantage of the inductive bias to explore in a directed manner, without assuming prior knowledge of the MDP. Empirical evaluations indicate a clear advantage of the proposed algorithm in terms of the rate of convergence and the final model fidelity when compared to intrinsic-motivation-based algorithms employing exploration bonuses such as prediction error and information gain. Moreover, our method maintains a computational advantage over a recent model-based active exploration (MAX) algorithm, by focusing on the information gain along trajectories instead of seeking a global exploration policy. A reference implementation of our algorithm and the conducted experiments is publicly available.

Probabilistic Trajectory Segmentation by Means of Hierarchical Dirichlet Process Switching Linear Dynamical Systems

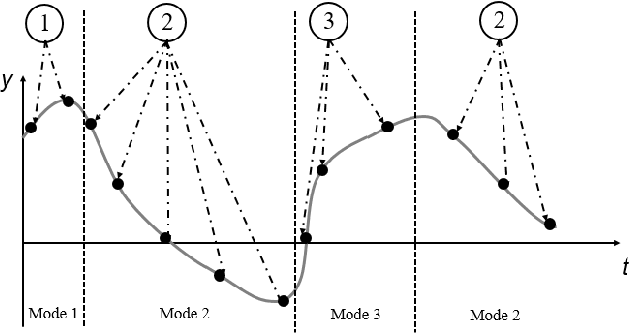
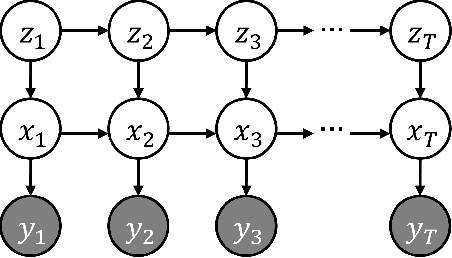
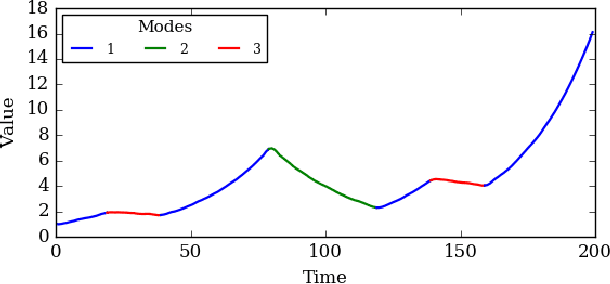
Using movement primitive libraries is an effective means to enable robots to solve more complex tasks. In order to build these movement libraries, current algorithms require a prior segmentation of the demonstration trajectories. A promising approach is to model the trajectory as being generated by a set of Switching Linear Dynamical Systems and inferring a meaningful segmentation by inspecting the transition points characterized by the switching dynamics. With respect to the learning, a nonparametric Bayesian approach is employed utilizing a Gibbs sampler.