Inverse Optimal Control Adapted to the Noise Characteristics of the Human Sensorimotor System
Paper and Code
Oct 21, 2021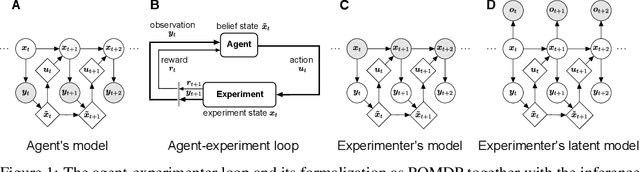

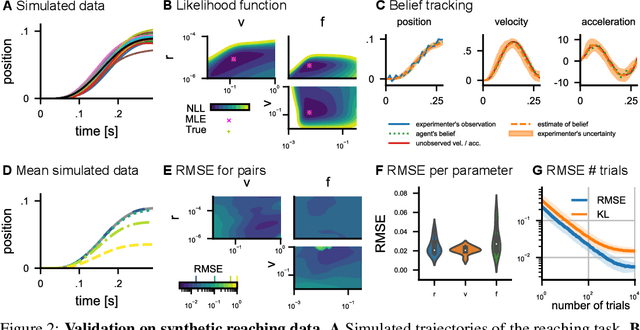
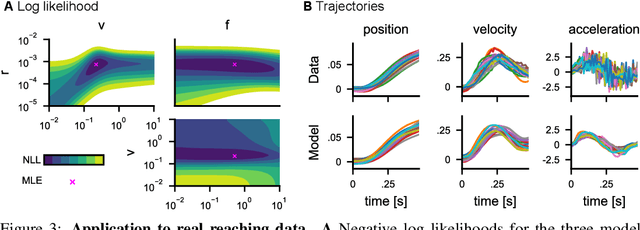
Computational level explanations based on optimal feedback control with signal-dependent noise have been able to account for a vast array of phenomena in human sensorimotor behavior. However, commonly a cost function needs to be assumed for a task and the optimality of human behavior is evaluated by comparing observed and predicted trajectories. Here, we introduce inverse optimal control with signal-dependent noise, which allows inferring the cost function from observed behavior. To do so, we formalize the problem as a partially observable Markov decision process and distinguish between the agent's and the experimenter's inference problems. Specifically, we derive a probabilistic formulation of the evolution of states and belief states and an approximation to the propagation equation in the linear-quadratic Gaussian problem with signal-dependent noise. We extend the model to the case of partial observability of state variables from the point of view of the experimenter. We show the feasibility of the approach through validation on synthetic data and application to experimental data. Our approach enables recovering the costs and benefits implicit in human sequential sensorimotor behavior, thereby reconciling normative and descriptive approaches in a computational framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge