Inverse decision-making using neural amortized Bayesian actors

Bayesian observer and actor models have provided normative explanations for many behavioral phenomena in perception, sensorimotor control, and other areas of cognitive science and neuroscience. They attribute behavioral variability and biases to different interpretable entities such as perceptual and motor uncertainty, prior beliefs, and behavioral costs. However, when extending these models to more complex tasks with continuous actions, solving the Bayesian decision-making problem is often analytically intractable. Moreover, inverting such models to perform inference over their parameters given behavioral data is computationally even more difficult. Therefore, researchers typically constrain their models to easily tractable components, such as Gaussian distributions or quadratic cost functions, or resort to numerical methods. To overcome these limitations, we amortize the Bayesian actor using a neural network trained on a wide range of different parameter settings in an unsupervised fashion. Using the pre-trained neural network enables performing gradient-based Bayesian inference of the Bayesian actor model's parameters. We show on synthetic data that the inferred posterior distributions are in close alignment with those obtained using analytical solutions where they exist. Where no analytical solution is available, we recover posterior distributions close to the ground truth. We then show that identifiability problems between priors and costs can arise in more complex cost functions. Finally, we apply our method to empirical data and show that it explains systematic individual differences of behavioral patterns.

Probabilistic inverse optimal control with local linearization for non-linear partially observable systems

Inverse optimal control methods can be used to characterize behavior in sequential decision-making tasks. Most existing work, however, requires the control signals to be known, or is limited to fully-observable or linear systems. This paper introduces a probabilistic approach to inverse optimal control for stochastic non-linear systems with missing control signals and partial observability that unifies existing approaches. By using an explicit model of the noise characteristics of the sensory and control systems of the agent in conjunction with local linearization techniques, we derive an approximate likelihood for the model parameters, which can be computed within a single forward pass. We evaluate our proposed method on stochastic and partially observable version of classic control tasks, a navigation task, and a manual reaching task. The proposed method has broad applicability, ranging from imitation learning to sensorimotor neuroscience.

Inverse Optimal Control Adapted to the Noise Characteristics of the Human Sensorimotor System

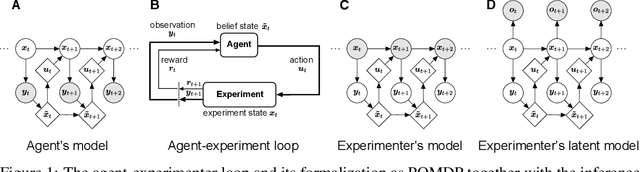
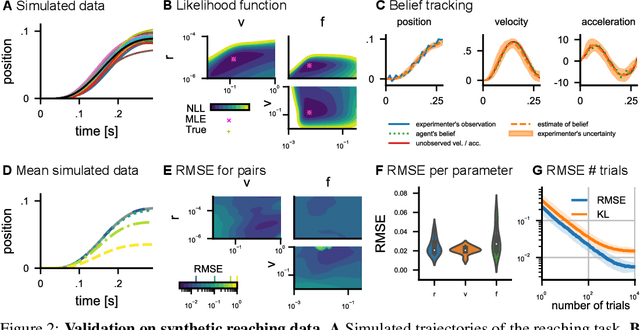
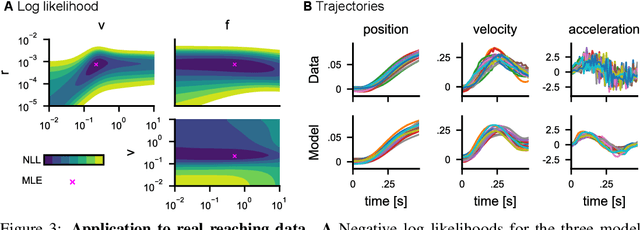
Computational level explanations based on optimal feedback control with signal-dependent noise have been able to account for a vast array of phenomena in human sensorimotor behavior. However, commonly a cost function needs to be assumed for a task and the optimality of human behavior is evaluated by comparing observed and predicted trajectories. Here, we introduce inverse optimal control with signal-dependent noise, which allows inferring the cost function from observed behavior. To do so, we formalize the problem as a partially observable Markov decision process and distinguish between the agent's and the experimenter's inference problems. Specifically, we derive a probabilistic formulation of the evolution of states and belief states and an approximation to the propagation equation in the linear-quadratic Gaussian problem with signal-dependent noise. We extend the model to the case of partial observability of state variables from the point of view of the experimenter. We show the feasibility of the approach through validation on synthetic data and application to experimental data. Our approach enables recovering the costs and benefits implicit in human sequential sensorimotor behavior, thereby reconciling normative and descriptive approaches in a computational framework.