Approximate Control for Continuous-Time POMDPs

This work proposes a decision-making framework for partially observable systems in continuous time with discrete state and action spaces. As optimal decision-making becomes intractable for large state spaces we employ approximation methods for the filtering and the control problem that scale well with an increasing number of states. Specifically, we approximate the high-dimensional filtering distribution by projecting it onto a parametric family of distributions, and integrate it into a control heuristic based on the fully observable system to obtain a scalable policy. We demonstrate the effectiveness of our approach on several partially observed systems, including queueing systems and chemical reaction networks.

Collaborative Optimization of the Age of Information under Partial Observability

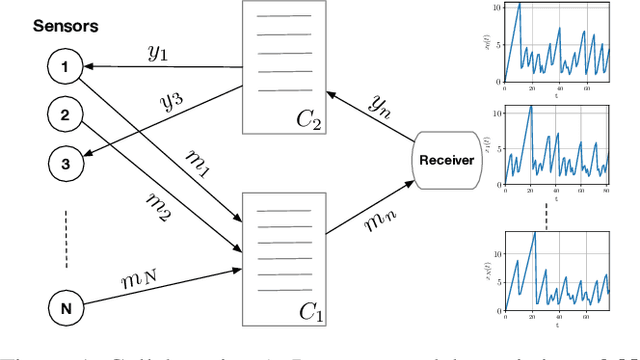
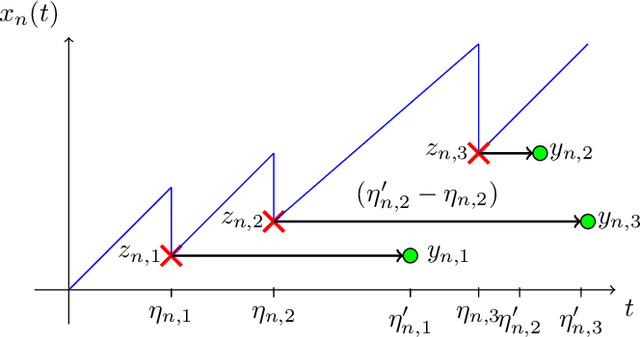
The significance of the freshness of sensor and control data at the receiver side, often referred to as Age of Information (AoI), is fundamentally constrained by contention for limited network resources. Evidently, network congestion is detrimental for AoI, where this congestion is partly self-induced by the sensor transmission process in addition to the contention from other transmitting sensors. In this work, we devise a decentralized AoI-minimizing transmission policy for a number of sensor agents sharing capacity-limited, non-FIFO duplex channels that introduce random delays in communication with a common receiver. By implementing the same policy, however with no explicit inter-agent communication, the agents minimize the expected AoI in this partially observable system. We cater to the partial observability due to random channel delays by designing a bootstrap particle filter that independently maintains a belief over the AoI of each agent. We also leverage mean-field control approximations and reinforcement learning to derive scalable and optimal solutions for minimizing the expected AoI collaboratively.

Entropic Matching for Expectation Propagation of Markov Jump Processes

This paper addresses the problem of statistical inference for latent continuous-time stochastic processes, which is often intractable, particularly for discrete state space processes described by Markov jump processes. To overcome this issue, we propose a new tractable inference scheme based on an entropic matching framework that can be embedded into the well-known expectation propagation algorithm. We demonstrate the effectiveness of our method by providing closed-form results for a simple family of approximate distributions and apply it to the general class of chemical reaction networks, which are a crucial tool for modeling in systems biology. Moreover, we derive closed form expressions for point estimation of the underlying parameters using an approximate expectation maximization procedure. We evaluate the performance of our method on various chemical reaction network instantiations, including a stochastic Lotka-Voltera example, and discuss its limitations and potential for future improvements. Our proposed approach provides a promising direction for addressing complex continuous-time Bayesian inference problems.

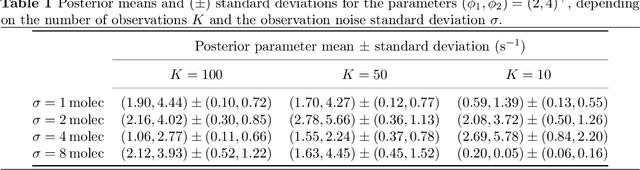
Bayesian Inference for Jump-Diffusion Approximations of Biochemical Reaction Networks

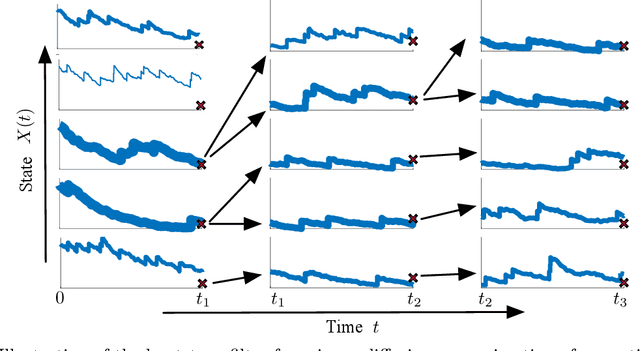
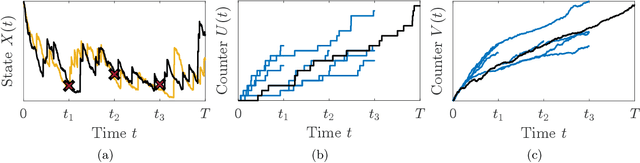
Biochemical reaction networks are an amalgamation of reactions where each reaction represents the interaction of different species. Generally, these networks exhibit a multi-scale behavior caused by the high variability in reaction rates and abundances of species. The so-called jump-diffusion approximation is a valuable tool in the modeling of such systems. The approximation is constructed by partitioning the reaction network into a fast and slow subgroup of fast and slow reactions, respectively. This enables the modeling of the dynamics using a Langevin equation for the fast group, while a Markov jump process model is kept for the dynamics of the slow group. Most often biochemical processes are poorly characterized in terms of parameters and population states. As a result of this, methods for estimating hidden quantities are of significant interest. In this paper, we develop a tractable Bayesian inference algorithm based on Markov chain Monte Carlo. The presented blocked Gibbs particle smoothing algorithm utilizes a sequential Monte Carlo method to estimate the latent states and performs distinct Gibbs steps for the parameters of a biochemical reaction network, by exploiting a jump-diffusion approximation model. The presented blocked Gibbs sampler is based on the two distinct steps of state inference and parameter inference. We estimate states via a continuous-time forward-filtering backward-smoothing procedure in the state inference step. By utilizing bootstrap particle filtering within a backward-smoothing procedure, we sample a smoothing trajectory. For estimating the hidden parameters, we utilize a separate Markov chain Monte Carlo sampler within the Gibbs sampler that uses the path-wise continuous-time representation of the reaction counters. Finally, the algorithm is numerically evaluated for a partially observed multi-scale birth-death process example.

Markov Chain Monte Carlo for Continuous-Time Switching Dynamical Systems

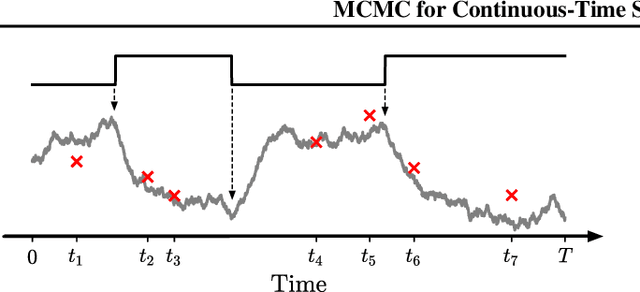
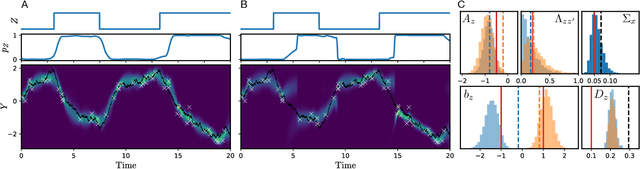
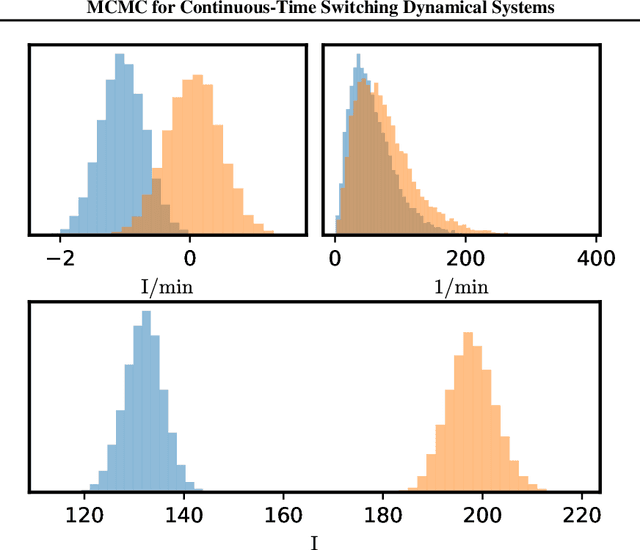
Switching dynamical systems are an expressive model class for the analysis of time-series data. As in many fields within the natural and engineering sciences, the systems under study typically evolve continuously in time, it is natural to consider continuous-time model formulations consisting of switching stochastic differential equations governed by an underlying Markov jump process. Inference in these types of models is however notoriously difficult, and tractable computational schemes are rare. In this work, we propose a novel inference algorithm utilizing a Markov Chain Monte Carlo approach. The presented Gibbs sampler allows to efficiently obtain samples from the exact continuous-time posterior processes. Our framework naturally enables Bayesian parameter estimation, and we also include an estimate for the diffusion covariance, which is oftentimes assumed fixed in stochastic differential equation models. We evaluate our framework under the modeling assumption and compare it against an existing variational inference approach.

Variational Inference for Continuous-Time Switching Dynamical Systems

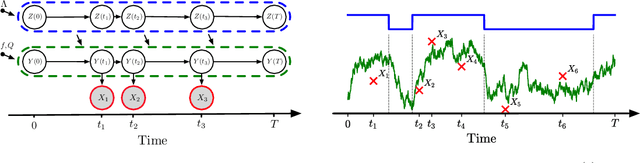
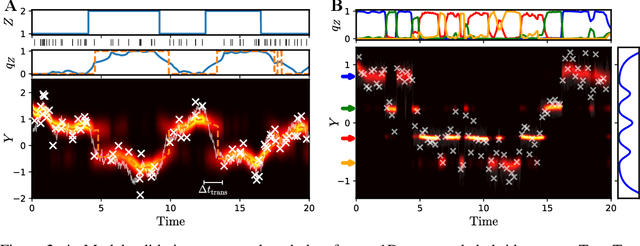
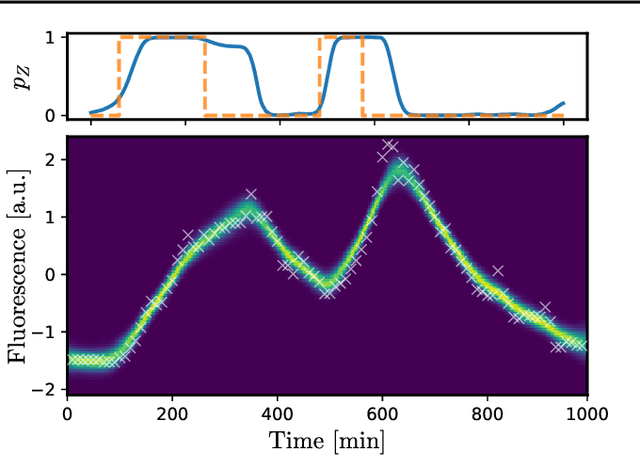
Switching dynamical systems provide a powerful, interpretable modeling framework for inference in time-series data in, e.g., the natural sciences or engineering applications. Since many areas, such as biology or discrete-event systems, are naturally described in continuous time, we present a model based on an Markov jump process modulating a subordinated diffusion process. We provide the exact evolution equations for the prior and posterior marginal densities, the direct solutions of which are however computationally intractable. Therefore, we develop a new continuous-time variational inference algorithm, combining a Gaussian process approximation on the diffusion level with posterior inference for Markov jump processes. By minimizing the path-wise Kullback-Leibler divergence we obtain (i) Bayesian latent state estimates for arbitrary points on the real axis and (ii) point estimates of unknown system parameters, utilizing variational expectation maximization. We extensively evaluate our algorithm under the model assumption and for real-world examples.

Scheduling in Parallel Finite Buffer Systems: Optimal Decisions under Delayed Feedback

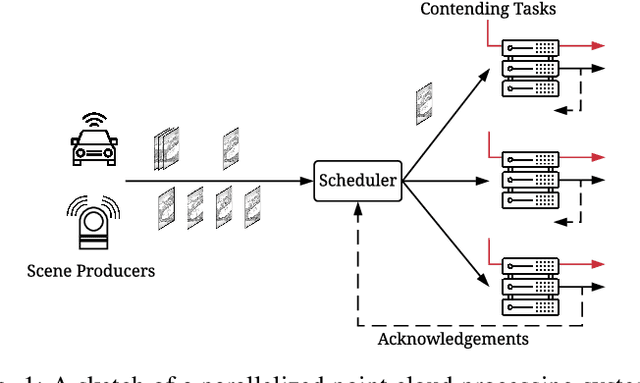
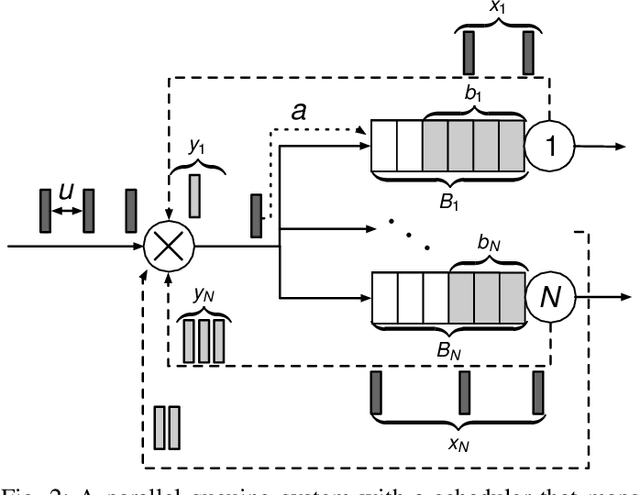
Scheduling decisions in parallel queuing systems arise as a fundamental problem, underlying the dimensioning and operation of many computing and communication systems, such as job routing in data center clusters, multipath communication, and Big Data systems. In essence, the scheduler maps each arriving job to one of the possibly heterogeneous servers while aiming at an optimization goal such as load balancing, low average delay or low loss rate. One main difficulty in finding optimal scheduling decisions here is that the scheduler only partially observes the impact of its decisions, e.g., through the delayed acknowledgements of the served jobs. In this paper, we provide a partially observable (PO) model that captures the scheduling decisions in parallel queuing systems under limited information of delayed acknowledgements. We present a simulation model for this PO system to find a near-optimal scheduling policy in real-time using a scalable Monte Carlo tree search algorithm. We numerically show that the resulting policy outperforms other limited information scheduling strategies such as variants of Join-the-Most-Observations and has comparable performance to full information strategies like: Join-the-Shortest-Queue, Join-the- Shortest-Queue(d) and Shortest-Expected-Delay. Finally, we show how our approach can optimise the real-time parallel processing by using network data provided by Kaggle.

POMDPs in Continuous Time and Discrete Spaces

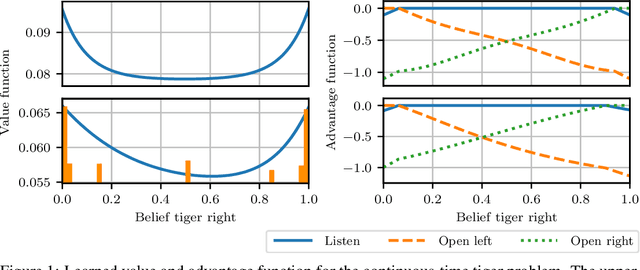
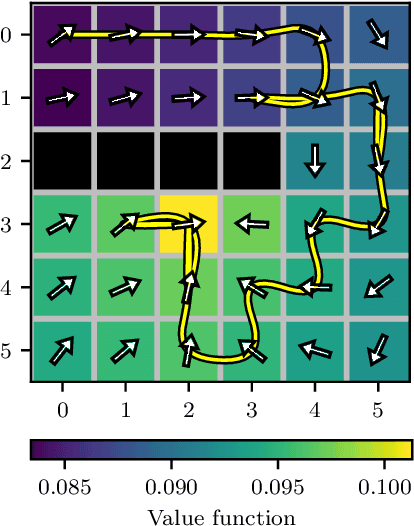
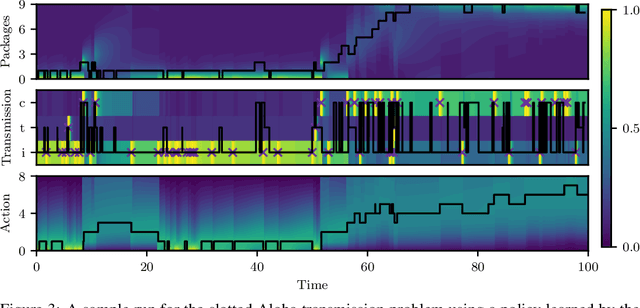
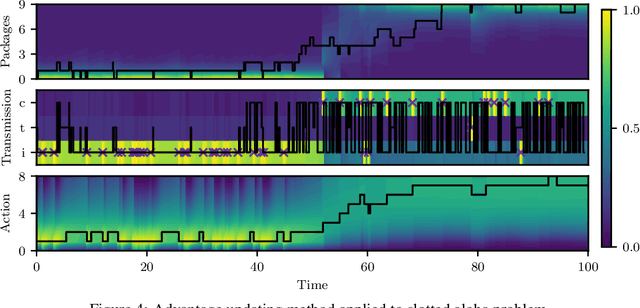
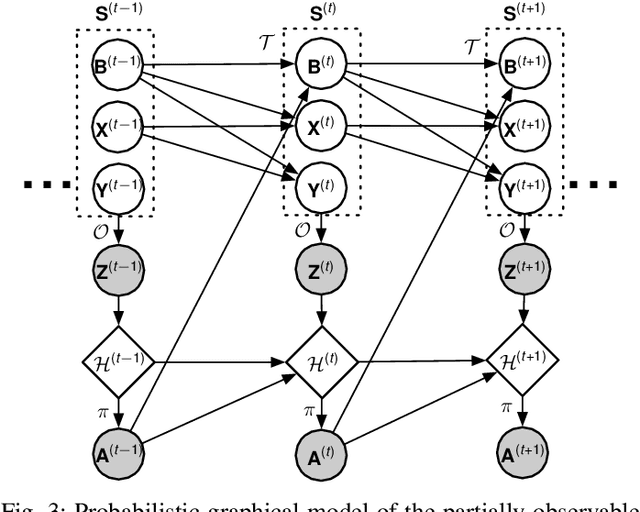
Many processes, such as discrete event systems in engineering or population dynamics in biology, evolve in discrete space and continuous time. We consider the problem of optimal decision making in such discrete state and action space systems under partial observability. This places our work at the intersection of optimal filtering and optimal control. At the current state of research, a mathematical description for simultaneous decision making and filtering in continuous time with finite state and action spaces is still missing. In this paper, we give a mathematical description of a continuous-time partial observable Markov decision process (POMDP). By leveraging optimal filtering theory we derive a Hamilton-Jacobi-Bellman (HJB) type equation that characterizes the optimal solution. Using techniques from deep learning we approximately solve the resulting partial integro-differential equation. We present (i) an approach solving the decision problem offline by learning an approximation of the value function and (ii) an online algorithm which provides a solution in belief space using deep reinforcement learning. We show the applicability on a set of toy examples which pave the way for future methods providing solutions for high dimensional problems.

Correlation Priors for Reinforcement Learning

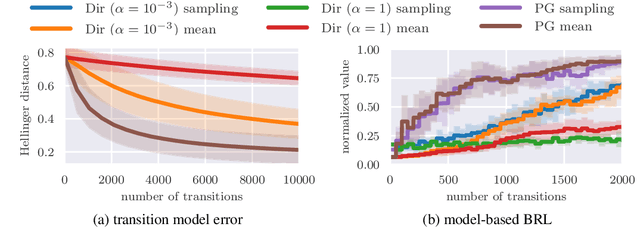
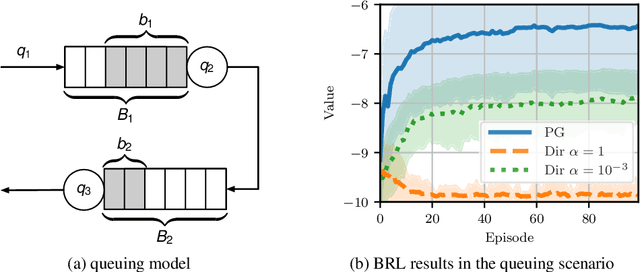
Many decision-making problems naturally exhibit pronounced structures inherited from the underlying characteristics of the environment. In a Markov decision process model, for example, two distinct states can have inherently related semantics or encode resembling physical state configurations, often implying locally correlated transition dynamics among the states. In order to complete a certain task, an agent acting in such environments needs to execute a series of temporally and spatially correlated actions. Though there exists a variety of approaches to account for correlations in continuous state-action domains, a principled solution for discrete environments is missing. In this work, we present a Bayesian learning framework based on P\'olya-Gamma augmentation that enables an analogous reasoning in such cases. We demonstrate the framework on a number of common decision-making related tasks, such as reinforcement learning, imitation learning and system identification. By explicitly modeling the underlying correlation structures, the proposed approach yields superior predictive performance compared to correlation-agnostic models, even when trained on data sets that are up to an order of magnitude smaller in size.