Bounded Rationality Equilibrium Learning in Mean Field Games

Mean field games (MFGs) tractably model behavior in large agent populations. The literature on learning MFG equilibria typically focuses on finding Nash equilibria (NE), which assume perfectly rational agents and are hence implausible in many realistic situations. To overcome these limitations, we incorporate bounded rationality into MFGs by leveraging the well-known concept of quantal response equilibria (QRE). Two novel types of MFG QRE enable the modeling of large agent populations where individuals only noisily estimate the true objective. We also introduce a second source of bounded rationality to MFGs by restricting agents' planning horizon. The resulting novel receding horizon (RH) MFGs are combined with QRE and existing approaches to model different aspects of bounded rationality in MFGs. We formally define MFG QRE and RH MFGs and compare them to existing equilibrium concepts such as entropy-regularized NE. Subsequently, we design generalized fixed point iteration and fictitious play algorithms to learn QRE and RH equilibria. After a theoretical analysis, we give different examples to evaluate the capabilities of our learning algorithms and outline practical differences between the equilibrium concepts.

Approximate Control for Continuous-Time POMDPs

This work proposes a decision-making framework for partially observable systems in continuous time with discrete state and action spaces. As optimal decision-making becomes intractable for large state spaces we employ approximation methods for the filtering and the control problem that scale well with an increasing number of states. Specifically, we approximate the high-dimensional filtering distribution by projecting it onto a parametric family of distributions, and integrate it into a control heuristic based on the fully observable system to obtain a scalable policy. We demonstrate the effectiveness of our approach on several partially observed systems, including queueing systems and chemical reaction networks.

A Survey on Large-Population Systems and Scalable Multi-Agent Reinforcement Learning

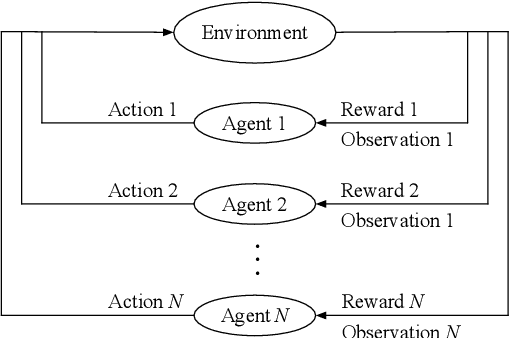
The analysis and control of large-population systems is of great interest to diverse areas of research and engineering, ranging from epidemiology over robotic swarms to economics and finance. An increasingly popular and effective approach to realizing sequential decision-making in multi-agent systems is through multi-agent reinforcement learning, as it allows for an automatic and model-free analysis of highly complex systems. However, the key issue of scalability complicates the design of control and reinforcement learning algorithms particularly in systems with large populations of agents. While reinforcement learning has found resounding empirical success in many scenarios with few agents, problems with many agents quickly become intractable and necessitate special consideration. In this survey, we will shed light on current approaches to tractably understanding and analyzing large-population systems, both through multi-agent reinforcement learning and through adjacent areas of research such as mean-field games, collective intelligence, or complex network theory. These classically independent subject areas offer a variety of approaches to understanding or modeling large-population systems, which may be of great use for the formulation of tractable MARL algorithms in the future. Finally, we survey potential areas of application for large-scale control and identify fruitful future applications of learning algorithms in practical systems. We hope that our survey could provide insight and future directions to junior and senior researchers in theoretical and applied sciences alike.