Bounded Rationality Equilibrium Learning in Mean Field Games

Mean field games (MFGs) tractably model behavior in large agent populations. The literature on learning MFG equilibria typically focuses on finding Nash equilibria (NE), which assume perfectly rational agents and are hence implausible in many realistic situations. To overcome these limitations, we incorporate bounded rationality into MFGs by leveraging the well-known concept of quantal response equilibria (QRE). Two novel types of MFG QRE enable the modeling of large agent populations where individuals only noisily estimate the true objective. We also introduce a second source of bounded rationality to MFGs by restricting agents' planning horizon. The resulting novel receding horizon (RH) MFGs are combined with QRE and existing approaches to model different aspects of bounded rationality in MFGs. We formally define MFG QRE and RH MFGs and compare them to existing equilibrium concepts such as entropy-regularized NE. Subsequently, we design generalized fixed point iteration and fictitious play algorithms to learn QRE and RH equilibria. After a theoretical analysis, we give different examples to evaluate the capabilities of our learning algorithms and outline practical differences between the equilibrium concepts.

Learning Mean Field Games on Sparse Graphs: A Hybrid Graphex Approach

Learning the behavior of large agent populations is an important task for numerous research areas. Although the field of multi-agent reinforcement learning (MARL) has made significant progress towards solving these systems, solutions for many agents often remain computationally infeasible and lack theoretical guarantees. Mean Field Games (MFGs) address both of these issues and can be extended to Graphon MFGs (GMFGs) to include network structures between agents. Despite their merits, the real world applicability of GMFGs is limited by the fact that graphons only capture dense graphs. Since most empirically observed networks show some degree of sparsity, such as power law graphs, the GMFG framework is insufficient for capturing these network topologies. Thus, we introduce the novel concept of Graphex MFGs (GXMFGs) which builds on the graph theoretical concept of graphexes. Graphexes are the limiting objects to sparse graph sequences that also have other desirable features such as the small world property. Learning equilibria in these games is challenging due to the rich and sparse structure of the underlying graphs. To tackle these challenges, we design a new learning algorithm tailored to the GXMFG setup. This hybrid graphex learning approach leverages that the system mainly consists of a highly connected core and a sparse periphery. After defining the system and providing a theoretical analysis, we state our learning approach and demonstrate its learning capabilities on both synthetic graphs and real-world networks. This comparison shows that our GXMFG learning algorithm successfully extends MFGs to a highly relevant class of hard, realistic learning problems that are not accurately addressed by current MARL and MFG methods.

Learning Decentralized Partially Observable Mean Field Control for Artificial Collective Behavior

Recent reinforcement learning (RL) methods have achieved success in various domains. However, multi-agent RL (MARL) remains a challenge in terms of decentralization, partial observability and scalability to many agents. Meanwhile, collective behavior requires resolution of the aforementioned challenges, and remains of importance to many state-of-the-art applications such as active matter physics, self-organizing systems, opinion dynamics, and biological or robotic swarms. Here, MARL via mean field control (MFC) offers a potential solution to scalability, but fails to consider decentralized and partially observable systems. In this paper, we enable decentralized behavior of agents under partial information by proposing novel models for decentralized partially observable MFC (Dec-POMFC), a broad class of problems with permutation-invariant agents allowing for reduction to tractable single-agent Markov decision processes (MDP) with single-agent RL solution. We provide rigorous theoretical results, including a dynamic programming principle, together with optimality guarantees for Dec-POMFC solutions applied to finite swarms of interest. Algorithmically, we propose Dec-POMFC-based policy gradient methods for MARL via centralized training and decentralized execution, together with policy gradient approximation guarantees. In addition, we improve upon state-of-the-art histogram-based MFC by kernel methods, which is of separate interest also for fully observable MFC. We evaluate numerically on representative collective behavior tasks such as adapted Kuramoto and Vicsek swarming models, being on par with state-of-the-art MARL. Overall, our framework takes a step towards RL-based engineering of artificial collective behavior via MFC.

UAV Swarms for Joint Data Ferrying and Dynamic Cell Coverage via Optimal Transport Descent and Quadratic Assignment

Both data ferrying with disruption-tolerant networking (DTN) and mobile cellular base stations constitute important techniques for UAV-aided communication in situations of crises where standard communication infrastructure is unavailable. For optimal use of a limited number of UAVs, we propose providing both DTN and a cellular base station on each UAV. Here, DTN is used for large amounts of low-priority data, while capacity-constrained cell coverage remains reserved for emergency calls or command and control. We optimize cell coverage via a novel optimal transport-based formulation using alternating minimization, while for data ferrying we periodically deliver data between dynamic clusters by solving quadratic assignment problems. In our evaluation, we consider different scenarios with varying mobility models and a wide range of flight patterns. Overall, we tractably achieve optimal cell coverage under quality-of-service costs with DTN-based data ferrying, enabling large-scale deployment of UAV swarms for crisis communication.

Multi-Agent Reinforcement Learning via Mean Field Control: Common Noise, Major Agents and Approximation Properties

Recently, mean field control (MFC) has provided a tractable and theoretically founded approach to otherwise difficult cooperative multi-agent control. However, the strict assumption of many independent, homogeneous agents may be too stringent in practice. In this work, we propose a novel discrete-time generalization of Markov decision processes and MFC to both many minor agents and potentially complex major agents -- major-minor mean field control (M3FC). In contrast to deterministic MFC, M3FC allows for stochastic minor agent distributions with strong correlation between minor agents through the major agent state, which can model arbitrary problem details not bound to any agent. Theoretically, we give rigorous approximation properties with novel proofs for both M3FC and existing MFC models in the finite multi-agent problem, together with a dynamic programming principle for solving such problems. In the infinite-horizon discounted case, existence of an optimal stationary policy follows. Algorithmically, we propose the major-minor mean field proximal policy optimization algorithm (M3FPPO) as a novel multi-agent reinforcement learning algorithm and demonstrate its success in illustrative M3FC-type problems.

Scalable Task-Driven Robotic Swarm Control via Collision Avoidance and Learning Mean-Field Control

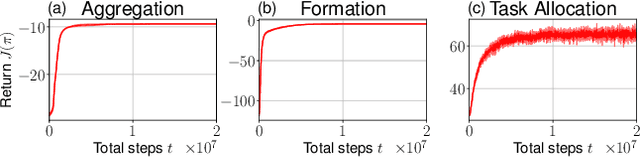
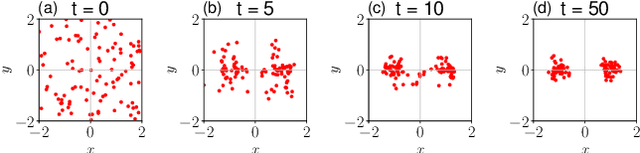
In recent years, reinforcement learning and its multi-agent analogue have achieved great success in solving various complex control problems. However, multi-agent reinforcement learning remains challenging both in its theoretical analysis and empirical design of algorithms, especially for large swarms of embodied robotic agents where a definitive toolchain remains part of active research. We use emerging state-of-the-art mean-field control techniques in order to convert many-agent swarm control into more classical single-agent control of distributions. This allows profiting from advances in single-agent reinforcement learning at the cost of assuming weak interaction between agents. As a result, the mean-field model is violated by the nature of real systems with embodied, physically colliding agents. Here, we combine collision avoidance and learning of mean-field control into a unified framework for tractably designing intelligent robotic swarm behavior. On the theoretical side, we provide novel approximation guarantees for both general mean-field control in continuous spaces and with collision avoidance. On the practical side, we show that our approach outperforms multi-agent reinforcement learning and allows for decentralized open-loop application while avoiding collisions, both in simulation and real UAV swarms. Overall, we propose a framework for the design of swarm behavior that is both mathematically well-founded and practically useful, enabling the solution of otherwise intractable swarm problems.

Mean Field Games on Weighted and Directed Graphs via Colored Digraphons

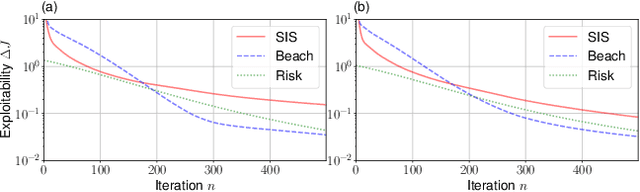
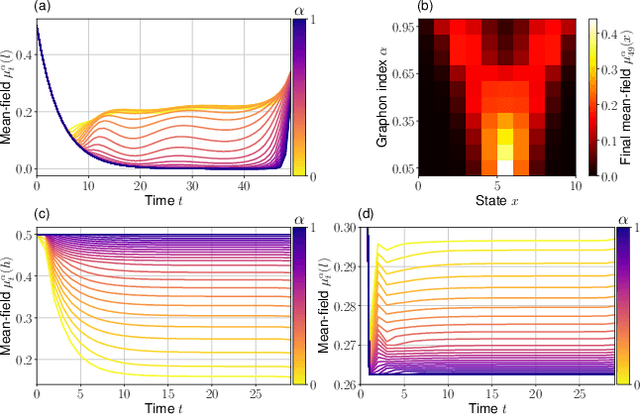
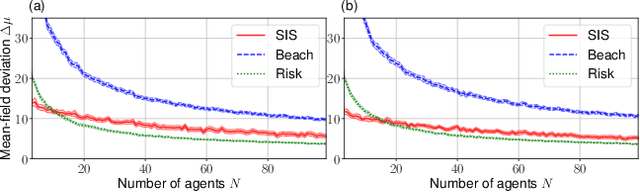
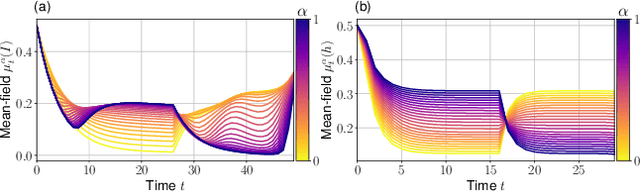
The field of multi-agent reinforcement learning (MARL) has made considerable progress towards controlling challenging multi-agent systems by employing various learning methods. Numerous of these approaches focus on empirical and algorithmic aspects of the MARL problems and lack a rigorous theoretical foundation. Graphon mean field games (GMFGs) on the other hand provide a scalable and mathematically well-founded approach to learning problems that involve a large number of connected agents. In standard GMFGs, the connections between agents are undirected, unweighted and invariant over time. Our paper introduces colored digraphon mean field games (CDMFGs) which allow for weighted and directed links between agents that are also adaptive over time. Thus, CDMFGs are able to model more complex connections than standard GMFGs. Besides a rigorous theoretical analysis including both existence and convergence guarantees, we provide a learning scheme and illustrate our findings with an epidemics model and a model of the systemic risk in financial markets.

Learning Sparse Graphon Mean Field Games

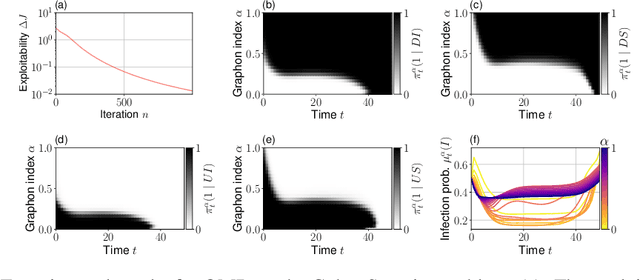
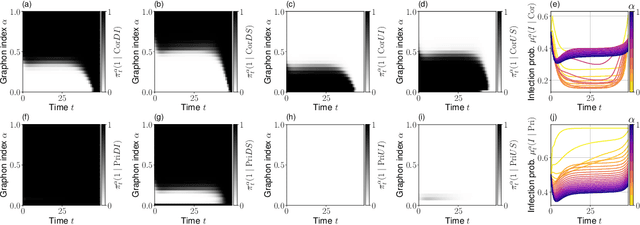
Although the field of multi-agent reinforcement learning (MARL) has made considerable progress in the last years, solving systems with a large number of agents remains a hard challenge. Graphon mean field games (GMFGs) enable the scalable analysis of MARL problems that are otherwise intractable. By the mathematical structure of graphons, this approach is limited to dense graphs which are insufficient to describe many real-world networks such as power law graphs. Our paper introduces a novel formulation of GMFGs, called LPGMFGs, which leverages the graph theoretical concept of $L^p$ graphons and provides a machine learning tool to efficiently and accurately approximate solutions for sparse network problems. This especially includes power law networks which are empirically observed in various application areas and cannot be captured by standard graphons. We derive theoretical existence and convergence guarantees and give empirical examples that demonstrate the accuracy of our learning approach for systems with many agents. Furthermore, we rigorously extend the Online Mirror Descent (OMD) learning algorithm to our setup to accelerate learning speed, allow for agent interaction through the mean field in the transition kernel, and empirically show its capabilities. In general, we provide a scalable, mathematically well-founded machine learning approach to a large class of otherwise intractable problems of great relevance in numerous research fields.