Mean Field Games on Weighted and Directed Graphs via Colored Digraphons
Paper and Code
Sep 08, 2022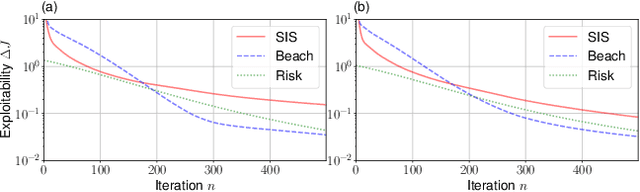
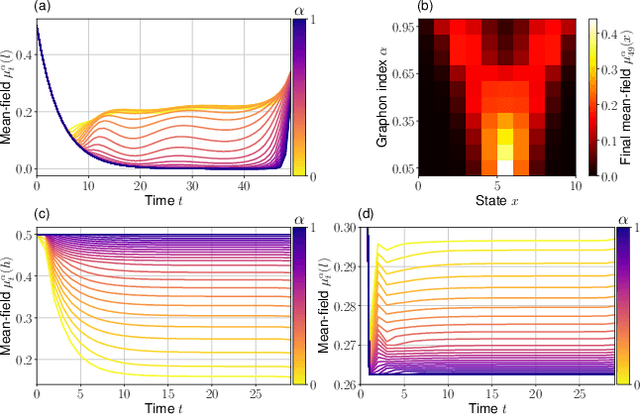
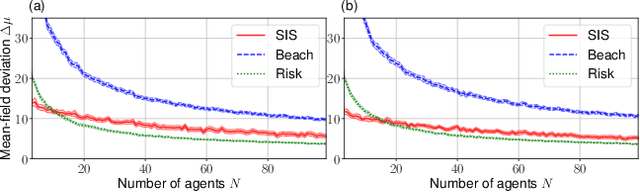
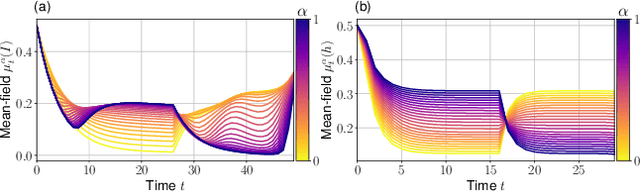
The field of multi-agent reinforcement learning (MARL) has made considerable progress towards controlling challenging multi-agent systems by employing various learning methods. Numerous of these approaches focus on empirical and algorithmic aspects of the MARL problems and lack a rigorous theoretical foundation. Graphon mean field games (GMFGs) on the other hand provide a scalable and mathematically well-founded approach to learning problems that involve a large number of connected agents. In standard GMFGs, the connections between agents are undirected, unweighted and invariant over time. Our paper introduces colored digraphon mean field games (CDMFGs) which allow for weighted and directed links between agents that are also adaptive over time. Thus, CDMFGs are able to model more complex connections than standard GMFGs. Besides a rigorous theoretical analysis including both existence and convergence guarantees, we provide a learning scheme and illustrate our findings with an epidemics model and a model of the systemic risk in financial markets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge