Correlation Priors for Reinforcement Learning

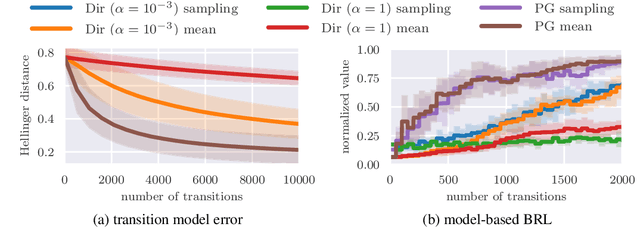
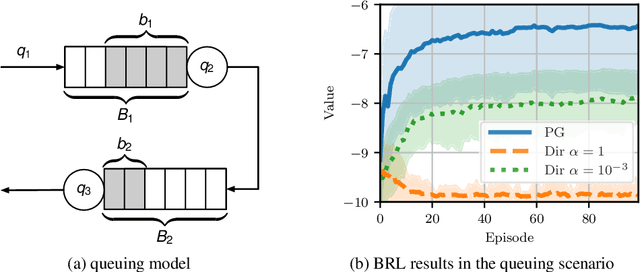
Many decision-making problems naturally exhibit pronounced structures inherited from the underlying characteristics of the environment. In a Markov decision process model, for example, two distinct states can have inherently related semantics or encode resembling physical state configurations, often implying locally correlated transition dynamics among the states. In order to complete a certain task, an agent acting in such environments needs to execute a series of temporally and spatially correlated actions. Though there exists a variety of approaches to account for correlations in continuous state-action domains, a principled solution for discrete environments is missing. In this work, we present a Bayesian learning framework based on P\'olya-Gamma augmentation that enables an analogous reasoning in such cases. We demonstrate the framework on a number of common decision-making related tasks, such as reinforcement learning, imitation learning and system identification. By explicitly modeling the underlying correlation structures, the proposed approach yields superior predictive performance compared to correlation-agnostic models, even when trained on data sets that are up to an order of magnitude smaller in size.