Matthew West
Leveraging Pre-trained and Transformer-derived Embeddings from EHRs to Characterize Heterogeneity Across Alzheimer's Disease and Related Dementias
Mar 30, 2024



Abstract:Alzheimer's disease is a progressive, debilitating neurodegenerative disease that affects 50 million people globally. Despite this substantial health burden, available treatments for the disease are limited and its fundamental causes remain poorly understood. Previous work has suggested the existence of clinically-meaningful sub-types, which it is suggested may correspond to distinct etiologies, disease courses, and ultimately appropriate treatments. Here, we use unsupervised learning techniques on electronic health records (EHRs) from a cohort of memory disorder patients to characterise heterogeneity in this disease population. Pre-trained embeddings for medical codes as well as transformer-derived Clinical BERT embeddings of free text are used to encode patient EHRs. We identify the existence of sub-populations on the basis of comorbidities and shared textual features, and discuss their clinical significance.
Learning from Integral Losses in Physics Informed Neural Networks
May 27, 2023Abstract:This work proposes a solution for the problem of training physics informed networks under partial integro-differential equations. These equations require infinite or a large number of neural evaluations to construct a single residual for training. As a result, accurate evaluation may be impractical, and we show that naive approximations at replacing these integrals with unbiased estimates lead to biased loss functions and solutions. To overcome this bias, we investigate three types of solutions: the deterministic sampling approach, the double-sampling trick, and the delayed target method. We consider three classes of PDEs for benchmarking; one defining a Poisson problem with singular charges and weak solutions, another involving weak solutions on electro-magnetic fields and a Maxwell equation, and a third one defining a Smoluchowski coagulation problem. Our numerical results confirm the existence of the aforementioned bias in practice, and also show that our proposed delayed target approach can lead to accurate solutions with comparable quality to ones estimated with a large number of samples. Our implementation is open-source and available at https://github.com/ehsansaleh/btspinn.
Hierarchical Graph Neural Network with Cross-Attention for Cross-Device User Matching
Apr 06, 2023Abstract:Cross-device user matching is a critical problem in numerous domains, including advertising, recommender systems, and cybersecurity. It involves identifying and linking different devices belonging to the same person, utilizing sequence logs. Previous data mining techniques have struggled to address the long-range dependencies and higher-order connections between the logs. Recently, researchers have modeled this problem as a graph problem and proposed a two-tier graph contextual embedding (TGCE) neural network architecture, which outperforms previous methods. In this paper, we propose a novel hierarchical graph neural network architecture (HGNN), which has a more computationally efficient second level design than TGCE. Furthermore, we introduce a cross-attention (Cross-Att) mechanism in our model, which improves performance by 5% compared to the state-of-the-art TGCE method.
MG-GNN: Multigrid Graph Neural Networks for Learning Multilevel Domain Decomposition Methods
Jan 26, 2023Abstract:Domain decomposition methods (DDMs) are popular solvers for discretized systems of partial differential equations (PDEs), with one-level and multilevel variants. These solvers rely on several algorithmic and mathematical parameters, prescribing overlap, subdomain boundary conditions, and other properties of the DDM. While some work has been done on optimizing these parameters, it has mostly focused on the one-level setting or special cases such as structured-grid discretizations with regular subdomain construction. In this paper, we propose multigrid graph neural networks (MG-GNN), a novel GNN architecture for learning optimized parameters in two-level DDMs\@. We train MG-GNN using a new unsupervised loss function, enabling effective training on small problems that yields robust performance on unstructured grids that are orders of magnitude larger than those in the training set. We show that MG-GNN outperforms popular hierarchical graph network architectures for this optimization and that our proposed loss function is critical to achieving this improved performance.
Truly Deterministic Policy Optimization
May 30, 2022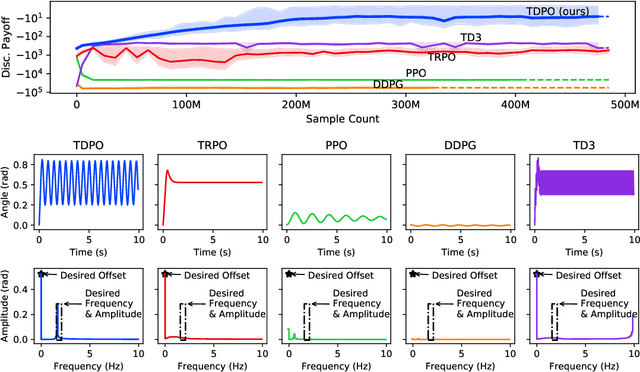

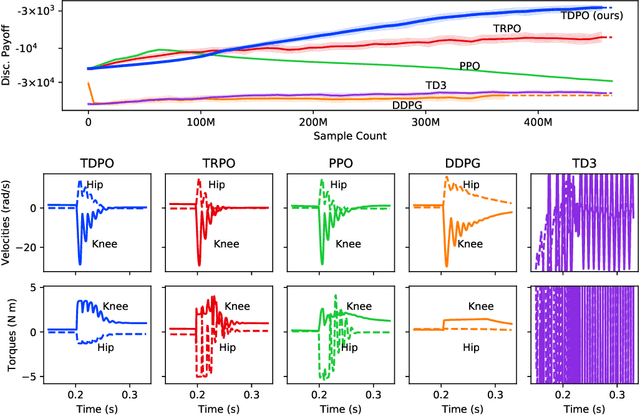

Abstract:In this paper, we present a policy gradient method that avoids exploratory noise injection and performs policy search over the deterministic landscape. By avoiding noise injection all sources of estimation variance can be eliminated in systems with deterministic dynamics (up to the initial state distribution). Since deterministic policy regularization is impossible using traditional non-metric measures such as the KL divergence, we derive a Wasserstein-based quadratic model for our purposes. We state conditions on the system model under which it is possible to establish a monotonic policy improvement guarantee, propose a surrogate function for policy gradient estimation, and show that it is possible to compute exact advantage estimates if both the state transition model and the policy are deterministic. Finally, we describe two novel robotic control environments -- one with non-local rewards in the frequency domain and the other with a long horizon (8000 time-steps) -- for which our policy gradient method (TDPO) significantly outperforms existing methods (PPO, TRPO, DDPG, and TD3). Our implementation with all the experimental settings is available at https://github.com/ehsansaleh/code_tdpo
Learning Interface Conditions in Domain Decomposition Solvers
May 19, 2022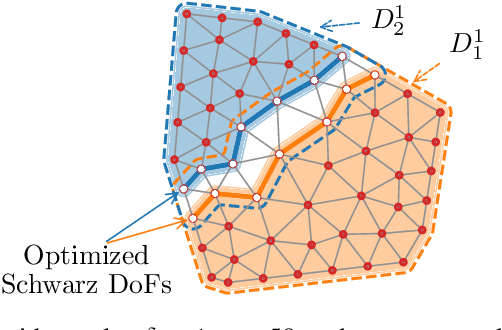
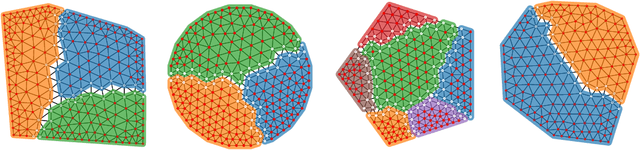
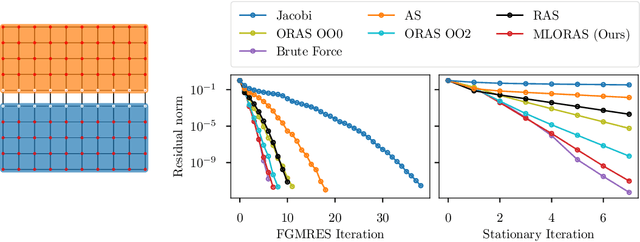
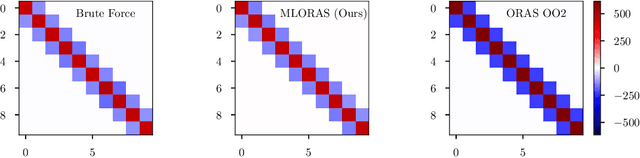
Abstract:Domain decomposition methods are widely used and effective in the approximation of solutions to partial differential equations. Yet the optimal construction of these methods requires tedious analysis and is often available only in simplified, structured-grid settings, limiting their use for more complex problems. In this work, we generalize optimized Schwarz domain decomposition methods to unstructured-grid problems, using Graph Convolutional Neural Networks (GCNNs) and unsupervised learning to learn optimal modifications at subdomain interfaces. A key ingredient in our approach is an improved loss function, enabling effective training on relatively small problems, but robust performance on arbitrarily large problems, with computational cost linear in problem size. The performance of the learned linear solvers is compared with both classical and optimized domain decomposition algorithms, for both structured- and unstructured-grid problems.
Efficient Partial Credit Grading of Proof Blocks Problems
Apr 08, 2022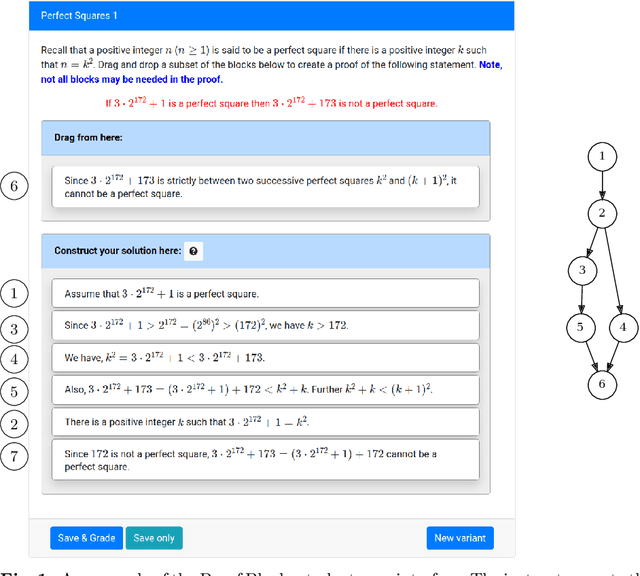
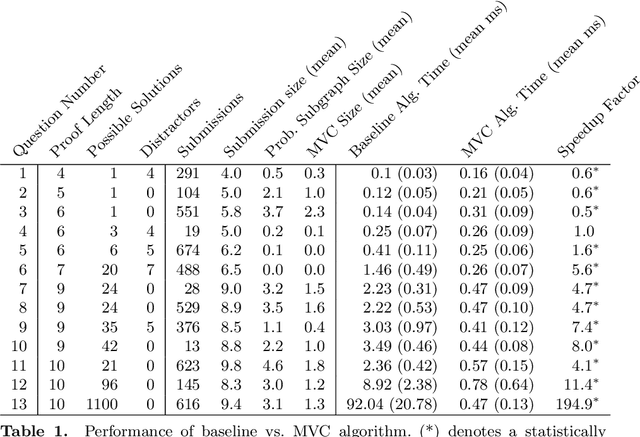
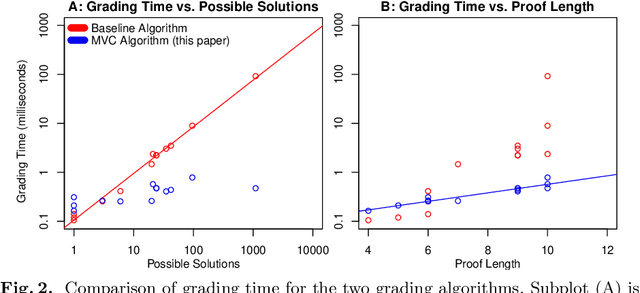
Abstract:Proof Blocks is a software tool which allows students to practice writing mathematical proofs by dragging and dropping lines instead of writing proofs from scratch. In this paper, we address the problem of assigning partial credit to students completing Proof Blocks problems. Because of the large solution space, it is computationally expensive to calculate the difference between an incorrect student solution and some correct solution, restricting the ability to automatically assign students partial credit. We propose a novel algorithm for finding the edit distance from an arbitrary student submission to some correct solution of a Proof Blocks problem. We benchmark our algorithm on thousands of student submissions from Fall 2020, showing that our novel algorithm can perform over 100 times better than the naive algorithm on real data. Our new algorithm has further applications in grading Parson's Problems, as well as any other kind of homework or exam problem where the solution space may be modeled as a directed acyclic graph.
Optimization-Based Algebraic Multigrid Coarsening Using Reinforcement Learning
Jun 03, 2021

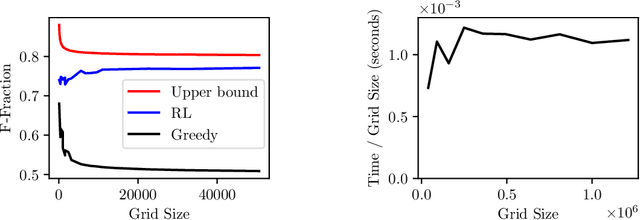
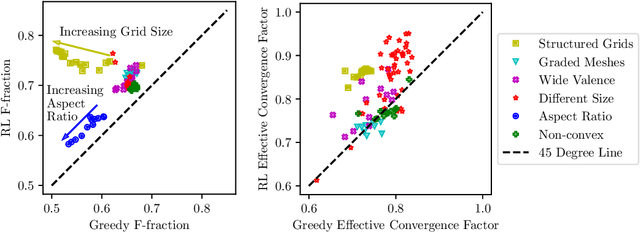
Abstract:Large sparse linear systems of equations are ubiquitous in science and engineering, such as those arising from discretizations of partial differential equations. Algebraic multigrid (AMG) methods are one of the most common methods of solving such linear systems, with an extensive body of underlying mathematical theory. A system of linear equations defines a graph on the set of unknowns and each level of a multigrid solver requires the selection of an appropriate coarse graph along with restriction and interpolation operators that map to and from the coarse representation. The efficiency of the multigrid solver depends critically on this selection and many selection methods have been developed over the years. Recently, it has been demonstrated that it is possible to directly learn the AMG interpolation and restriction operators, given a coarse graph selection. In this paper, we consider the complementary problem of learning to coarsen graphs for a multigrid solver. We propose a method using a reinforcement learning (RL) agent based on graph neural networks (GNNs), which can learn to perform graph coarsening on small training graphs and then be applied to unstructured large graphs. We demonstrate that this method can produce better coarse graphs than existing algorithms, even as the graph size increases and other properties of the graph are varied. We also propose an efficient inference procedure for performing graph coarsening that results in linear time complexity in graph size.
Local Navigation and Docking of an Autonomous Robot Mower using Reinforcement Learning and Computer Vision
Jan 15, 2021

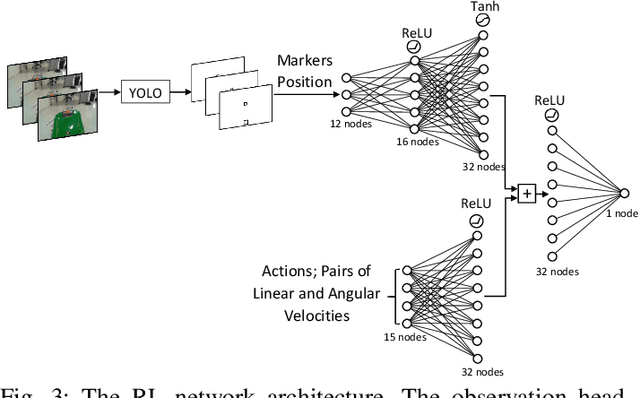
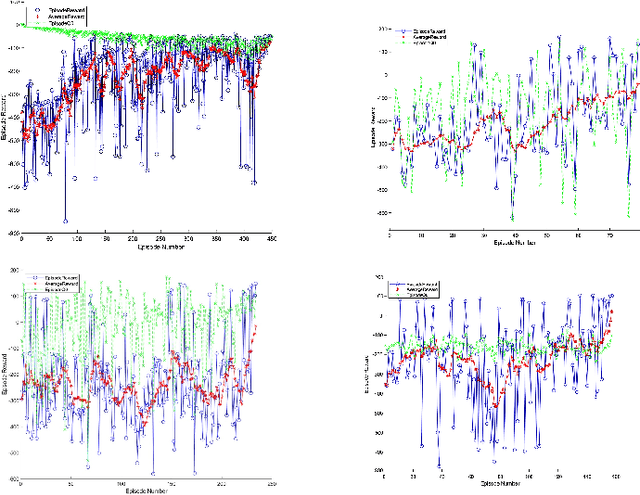
Abstract:We demonstrate a successful navigation and docking control system for the John Deere Tango autonomous mower, using only a single camera as the input. This vision-only system is of interest because it is inexpensive, simple for production, and requires no external sensing. This is in contrast to existing systems that rely on integrated position sensors and global positioning system (GPS) technologies. To produce our system we combined a state-of-the-art object detection architecture, YOLO, with a reinforcement learning (RL) architecture, Double Deep QNetworks (Double DQN). The object detection network identifies features on the mower and passes its output to the RL network, providing it with a low-dimensional representation that enables rapid and robust training. Finally, the RL network learns how to navigate the machine to the desired spot in a custom simulation environment. When tested on mower hardware the system is able to dock with centimeter-level accuracy from arbitrary initial locations and orientations.
Unsupervised Regionalization of Particle-resolved Aerosol Mixing State Indices on the Global Scale
Dec 06, 2020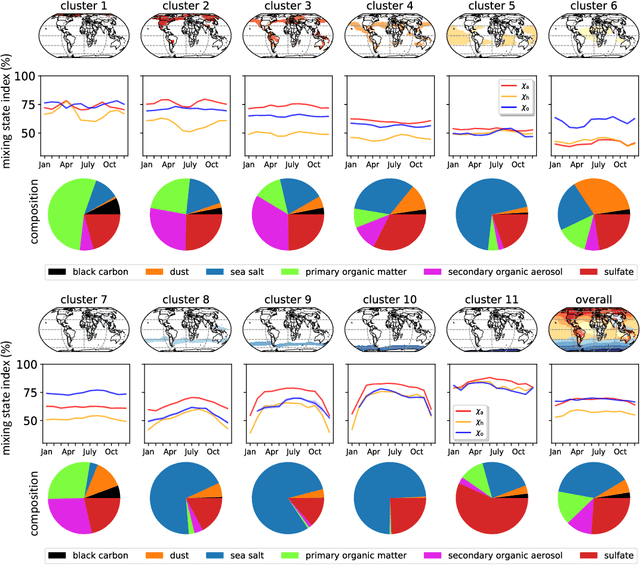
Abstract:The aerosol mixing state significantly affects the climate and health impacts of atmospheric aerosol particles. Simplified aerosol mixing state assumptions, common in Earth System models, can introduce errors in the prediction of these aerosol impacts. The aerosol mixing state index, a metric to quantify aerosol mixing state, is a convenient measure for quantifying these errors. Global estimates of aerosol mixing state indices have recently become available via supervised learning models, but require regionalization to ease spatiotemporal analysis. Here we developed a simple but effective unsupervised learning approach to regionalize predictions of global aerosol mixing state indices. We used the monthly average of aerosol mixing state indices global distribution as the input data. Grid cells were then clustered into regions by the k-means algorithm without explicit spatial information as input. This approach resulted in eleven regions over the globe with specific spatial aggregation patterns. Each region exhibited a unique distribution of mixing state indices and aerosol compositions, showing the effectiveness of the unsupervised regionalization approach. This study defines "aerosol mixing state zones" that could be useful for atmospheric science research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge