Scott MacLachlan
MG-GNN: Multigrid Graph Neural Networks for Learning Multilevel Domain Decomposition Methods
Jan 26, 2023Abstract:Domain decomposition methods (DDMs) are popular solvers for discretized systems of partial differential equations (PDEs), with one-level and multilevel variants. These solvers rely on several algorithmic and mathematical parameters, prescribing overlap, subdomain boundary conditions, and other properties of the DDM. While some work has been done on optimizing these parameters, it has mostly focused on the one-level setting or special cases such as structured-grid discretizations with regular subdomain construction. In this paper, we propose multigrid graph neural networks (MG-GNN), a novel GNN architecture for learning optimized parameters in two-level DDMs\@. We train MG-GNN using a new unsupervised loss function, enabling effective training on small problems that yields robust performance on unstructured grids that are orders of magnitude larger than those in the training set. We show that MG-GNN outperforms popular hierarchical graph network architectures for this optimization and that our proposed loss function is critical to achieving this improved performance.
Optimized Sparse Matrix Operations for Reverse Mode Automatic Differentiation
Dec 10, 2022



Abstract:Sparse matrix representations are ubiquitous in computational science and machine learning, leading to significant reductions in compute time, in comparison to dense representation, for problems that have local connectivity. The adoption of sparse representation in leading ML frameworks such as PyTorch is incomplete, however, with support for both automatic differentiation and GPU acceleration missing. In this work, we present an implementation of a CSR-based sparse matrix wrapper for PyTorch with CUDA acceleration for basic matrix operations, as well as automatic differentiability. We also present several applications of the resulting sparse kernels to optimization problems, demonstrating ease of implementation and performance measurements versus their dense counterparts.
Learning Interface Conditions in Domain Decomposition Solvers
May 19, 2022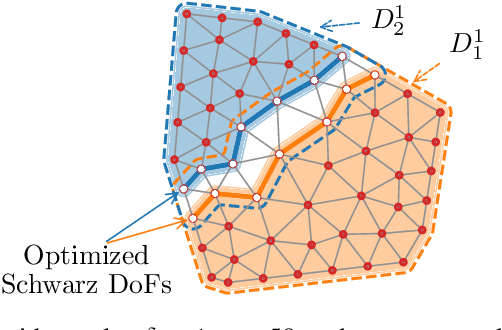
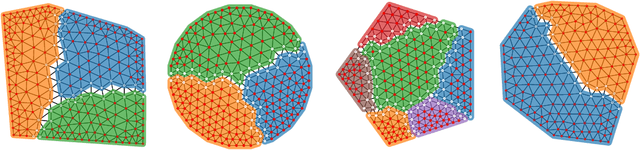
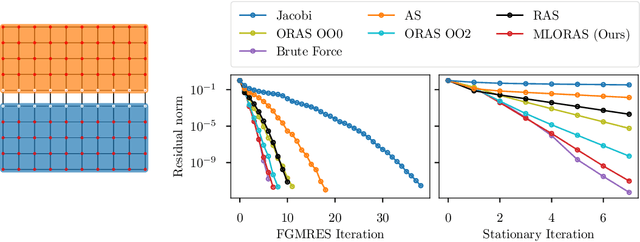
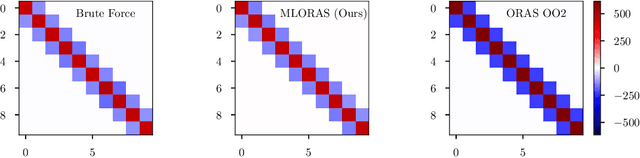
Abstract:Domain decomposition methods are widely used and effective in the approximation of solutions to partial differential equations. Yet the optimal construction of these methods requires tedious analysis and is often available only in simplified, structured-grid settings, limiting their use for more complex problems. In this work, we generalize optimized Schwarz domain decomposition methods to unstructured-grid problems, using Graph Convolutional Neural Networks (GCNNs) and unsupervised learning to learn optimal modifications at subdomain interfaces. A key ingredient in our approach is an improved loss function, enabling effective training on relatively small problems, but robust performance on arbitrarily large problems, with computational cost linear in problem size. The performance of the learned linear solvers is compared with both classical and optimized domain decomposition algorithms, for both structured- and unstructured-grid problems.
Optimization-Based Algebraic Multigrid Coarsening Using Reinforcement Learning
Jun 03, 2021

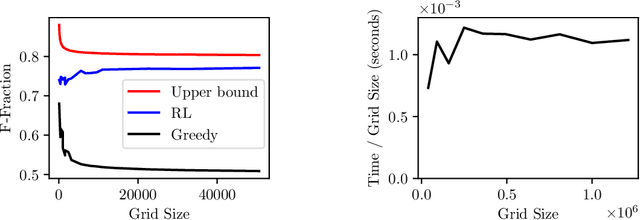
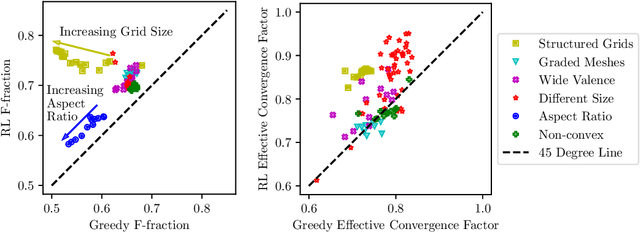
Abstract:Large sparse linear systems of equations are ubiquitous in science and engineering, such as those arising from discretizations of partial differential equations. Algebraic multigrid (AMG) methods are one of the most common methods of solving such linear systems, with an extensive body of underlying mathematical theory. A system of linear equations defines a graph on the set of unknowns and each level of a multigrid solver requires the selection of an appropriate coarse graph along with restriction and interpolation operators that map to and from the coarse representation. The efficiency of the multigrid solver depends critically on this selection and many selection methods have been developed over the years. Recently, it has been demonstrated that it is possible to directly learn the AMG interpolation and restriction operators, given a coarse graph selection. In this paper, we consider the complementary problem of learning to coarsen graphs for a multigrid solver. We propose a method using a reinforcement learning (RL) agent based on graph neural networks (GNNs), which can learn to perform graph coarsening on small training graphs and then be applied to unstructured large graphs. We demonstrate that this method can produce better coarse graphs than existing algorithms, even as the graph size increases and other properties of the graph are varied. We also propose an efficient inference procedure for performing graph coarsening that results in linear time complexity in graph size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge