Saba Ghaffari
Learning from Integral Losses in Physics Informed Neural Networks
May 27, 2023Abstract:This work proposes a solution for the problem of training physics informed networks under partial integro-differential equations. These equations require infinite or a large number of neural evaluations to construct a single residual for training. As a result, accurate evaluation may be impractical, and we show that naive approximations at replacing these integrals with unbiased estimates lead to biased loss functions and solutions. To overcome this bias, we investigate three types of solutions: the deterministic sampling approach, the double-sampling trick, and the delayed target method. We consider three classes of PDEs for benchmarking; one defining a Poisson problem with singular charges and weak solutions, another involving weak solutions on electro-magnetic fields and a Maxwell equation, and a third one defining a Smoluchowski coagulation problem. Our numerical results confirm the existence of the aforementioned bias in practice, and also show that our proposed delayed target approach can lead to accurate solutions with comparable quality to ones estimated with a large number of samples. Our implementation is open-source and available at https://github.com/ehsansaleh/btspinn.
Property-Guided Generative Modelling for Robust Model-Based Design with Imbalanced Data
May 23, 2023



Abstract:The problem of designing protein sequences with desired properties is challenging, as it requires to explore a high-dimensional protein sequence space with extremely sparse meaningful regions. This has led to the development of model-based optimization (MBO) techniques that aid in the design, by using effective search models guided by the properties over the sequence space. However, the intrinsic imbalanced nature of experimentally derived datasets causes existing MBO approaches to struggle or outright fail. We propose a property-guided variational auto-encoder (PGVAE) whose latent space is explicitly structured by the property values such that samples are prioritized according to these properties. Through extensive benchmarking on real and semi-synthetic protein datasets, we demonstrate that MBO with PGVAE robustly finds sequences with improved properties despite significant dataset imbalances. We further showcase the generality of our approach to continuous design spaces, and its robustness to dataset imbalance in an application to physics-informed neural networks.
Truly Deterministic Policy Optimization
May 30, 2022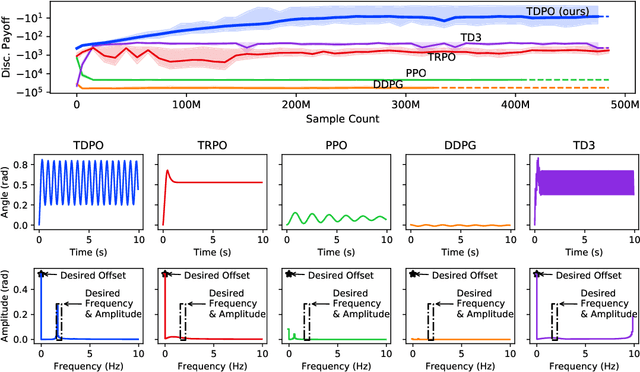

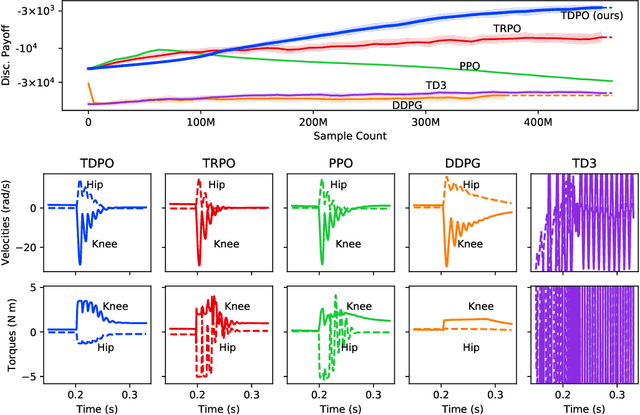

Abstract:In this paper, we present a policy gradient method that avoids exploratory noise injection and performs policy search over the deterministic landscape. By avoiding noise injection all sources of estimation variance can be eliminated in systems with deterministic dynamics (up to the initial state distribution). Since deterministic policy regularization is impossible using traditional non-metric measures such as the KL divergence, we derive a Wasserstein-based quadratic model for our purposes. We state conditions on the system model under which it is possible to establish a monotonic policy improvement guarantee, propose a surrogate function for policy gradient estimation, and show that it is possible to compute exact advantage estimates if both the state transition model and the policy are deterministic. Finally, we describe two novel robotic control environments -- one with non-local rewards in the frequency domain and the other with a long horizon (8000 time-steps) -- for which our policy gradient method (TDPO) significantly outperforms existing methods (PPO, TRPO, DDPG, and TD3). Our implementation with all the experimental settings is available at https://github.com/ehsansaleh/code_tdpo
On the Importance of Firth Bias Reduction in Few-Shot Classification
Oct 06, 2021
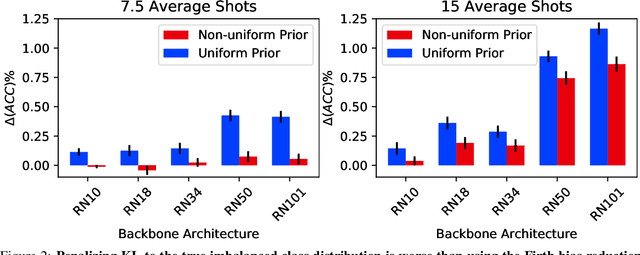

Abstract:Learning accurate classifiers for novel categories from very few examples, known as few-shot image classification, is a challenging task in statistical machine learning and computer vision. The performance in few-shot classification suffers from the bias in the estimation of classifier parameters; however, an effective underlying bias reduction technique that could alleviate this issue in training few-shot classifiers has been overlooked. In this work, we demonstrate the effectiveness of Firth bias reduction in few-shot classification. Theoretically, Firth bias reduction removes the first order term $O(N^{-1})$ from the small-sample bias of the Maximum Likelihood Estimator. Here we show that the general Firth bias reduction technique simplifies to encouraging uniform class assignment probabilities for multinomial logistic classification, and almost has the same effect in cosine classifiers. We derive the optimization objective for Firth penalized multinomial logistic and cosine classifiers, and empirically evaluate that it is consistently effective across the board for few-shot image classification, regardless of (1) the feature representations from different backbones, (2) the number of samples per class, and (3) the number of classes. Finally, we show the robustness of Firth bias reduction, in the case of imbalanced data distribution. Our implementation is available at https://github.com/ehsansaleh/firth_bias_reduction
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge