Yu-xiong Wang
Offline Imitation from Observation via Primal Wasserstein State Occupancy Matching
Nov 21, 2023Abstract:In real-world scenarios, arbitrary interactions with the environment can often be costly, and actions of expert demonstrations are not always available. To reduce the need for both, Offline Learning from Observations (LfO) is extensively studied, where the agent learns to solve a task with only expert states and \textit{task-agnostic} non-expert state-action pairs. The state-of-the-art DIstribution Correction Estimation (DICE) methods minimize the state occupancy divergence between the learner and expert policies. However, they are limited to either $f$-divergences (KL and $\chi^2$) or Wasserstein distance with Rubinstein duality, the latter of which constrains the underlying distance metric crucial to the performance of Wasserstein-based solutions. To address this problem, we propose Primal Wasserstein DICE (PW-DICE), which minimizes the primal Wasserstein distance between the expert and learner state occupancies with a pessimistic regularizer and leverages a contrastively learned distance as the underlying metric for the Wasserstein distance. Theoretically, we prove that our framework is a generalization of the state-of-the-art, SMODICE, and unifies $f$-divergence and Wasserstein minimization. Empirically, we find that PW-DICE improves upon several state-of-the-art methods on multiple testbeds.
On the Importance of Firth Bias Reduction in Few-Shot Classification
Oct 06, 2021
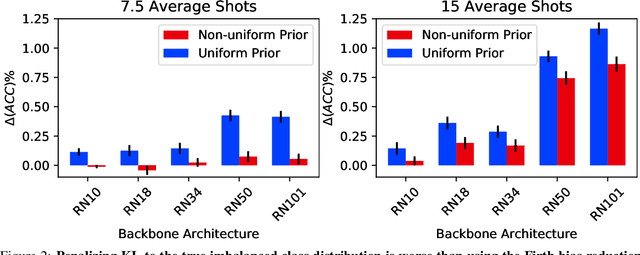

Abstract:Learning accurate classifiers for novel categories from very few examples, known as few-shot image classification, is a challenging task in statistical machine learning and computer vision. The performance in few-shot classification suffers from the bias in the estimation of classifier parameters; however, an effective underlying bias reduction technique that could alleviate this issue in training few-shot classifiers has been overlooked. In this work, we demonstrate the effectiveness of Firth bias reduction in few-shot classification. Theoretically, Firth bias reduction removes the first order term $O(N^{-1})$ from the small-sample bias of the Maximum Likelihood Estimator. Here we show that the general Firth bias reduction technique simplifies to encouraging uniform class assignment probabilities for multinomial logistic classification, and almost has the same effect in cosine classifiers. We derive the optimization objective for Firth penalized multinomial logistic and cosine classifiers, and empirically evaluate that it is consistently effective across the board for few-shot image classification, regardless of (1) the feature representations from different backbones, (2) the number of samples per class, and (3) the number of classes. Finally, we show the robustness of Firth bias reduction, in the case of imbalanced data distribution. Our implementation is available at https://github.com/ehsansaleh/firth_bias_reduction
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge