Autograding Mathematical Induction Proofs with Natural Language Processing

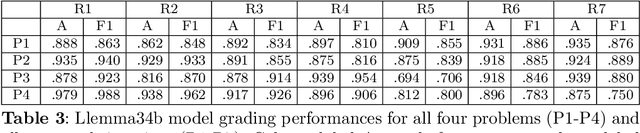
In mathematical proof education, there remains a need for interventions that help students learn to write mathematical proofs. Research has shown that timely feedback can be very helpful to students learning new skills. While for many years natural language processing models have struggled to perform well on tasks related to mathematical texts, recent developments in natural language processing have created the opportunity to complete the task of giving students instant feedback on their mathematical proofs. In this paper, we present a set of training methods and models capable of autograding freeform mathematical proofs by leveraging existing large language models and other machine learning techniques. The models are trained using proof data collected from four different proof by induction problems. We use four different robust large language models to compare their performances, and all achieve satisfactory performances to various degrees. Additionally, we recruit human graders to grade the same proofs as the training data, and find that the best grading model is also more accurate than most human graders. With the development of these grading models, we create and deploy an autograder for proof by induction problems and perform a user study with students. Results from the study shows that students are able to make significant improvements to their proofs using the feedback from the autograder, but students still do not trust the AI autograders as much as they trust human graders. Future work can improve on the autograder feedback and figure out ways to help students trust AI autograders.

Efficient Partial Credit Grading of Proof Blocks Problems

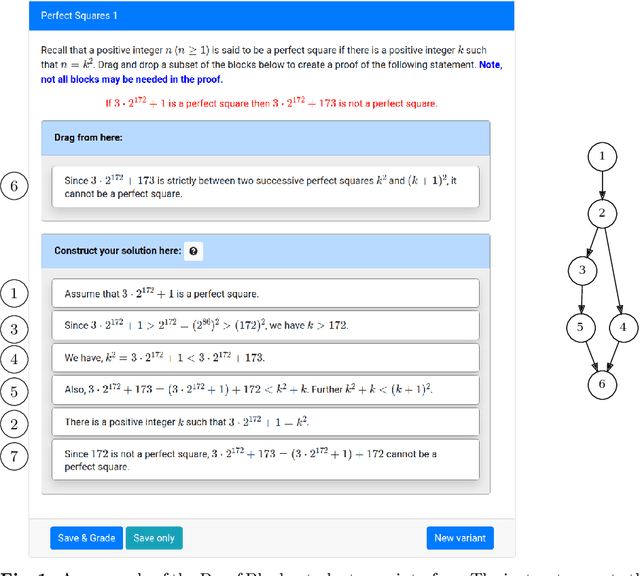
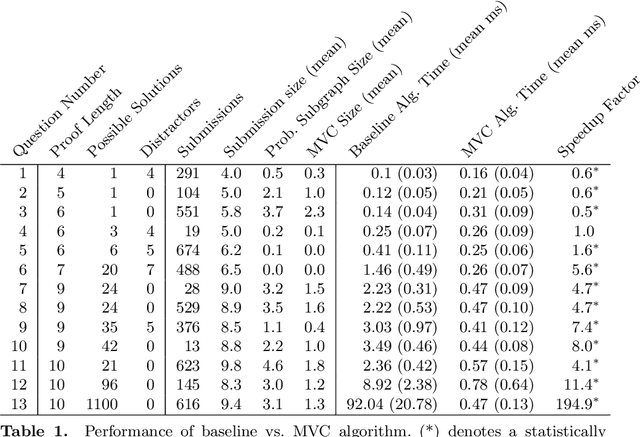
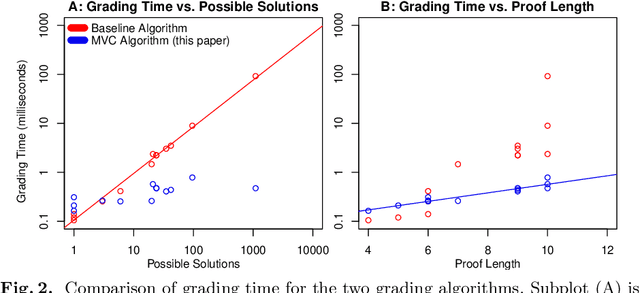
Proof Blocks is a software tool which allows students to practice writing mathematical proofs by dragging and dropping lines instead of writing proofs from scratch. In this paper, we address the problem of assigning partial credit to students completing Proof Blocks problems. Because of the large solution space, it is computationally expensive to calculate the difference between an incorrect student solution and some correct solution, restricting the ability to automatically assign students partial credit. We propose a novel algorithm for finding the edit distance from an arbitrary student submission to some correct solution of a Proof Blocks problem. We benchmark our algorithm on thousands of student submissions from Fall 2020, showing that our novel algorithm can perform over 100 times better than the naive algorithm on real data. Our new algorithm has further applications in grading Parson's Problems, as well as any other kind of homework or exam problem where the solution space may be modeled as a directed acyclic graph.