Applying Physics-Informed Enhanced Super-Resolution Generative Adversarial Networks to Finite-Rate-Chemistry Flows and Predicting Lean Premixed Gas Turbine Combustors

The accurate prediction of small scales in underresolved flows is still one of the main challenges in predictive simulations of complex configurations. Over the last few years, data-driven modeling has become popular in many fields as large, often extensively labeled datasets are now available and training of large neural networks has become possible on graphics processing units (GPUs) that speed up the learning process tremendously. In fact, the successful application of deep neural networks in fluid dynamics, such as for underresolved reactive flows, is still challenging. This work advances the recently introduced PIESRGAN to reactive finite-rate-chemistry flows. However, since combustion chemistry typically acts on the smallest scales, the original approach needs to be extended. Therefore, the modeling approach of PIESRGAN is modified to accurately account for the challenges in the context of laminar finite-rate-chemistry flows. The modified PIESRGAN-based model gives good agreement in a priori and a posteriori tests in a laminar lean premixed combustion setup. Furthermore, a reduced PIESRGAN-based model is presented that solves only the major species on a reconstructed field and employs PIERSGAN lookup for the remaining species, utilizing staggering in time. The advantages of the discriminator-supported training are shown, and the usability of the new model demonstrated in the context of a model gas turbine combustor.

Applying Physics-Informed Enhanced Super-Resolution Generative Adversarial Networks to Turbulent Premixed Combustion and Engine-like Flame Kernel Direct Numerical Simulation Data

Models for finite-rate-chemistry in underresolved flows still pose one of the main challenges for predictive simulations of complex configurations. The problem gets even more challenging if turbulence is involved. This work advances the recently developed PIESRGAN modeling approach to turbulent premixed combustion. For that, the physical information processed by the network and considered in the loss function are adjusted, the training process is smoothed, and especially effects from density changes are considered. The resulting model provides good results for a priori and a posteriori tests on direct numerical simulation data of a fully turbulent premixed flame kernel. The limits of the modeling approach are discussed. Finally, the model is employed to compute further realizations of the premixed flame kernel, which are analyzed with a scale-sensitive framework regarding their cycle-to-cycle variations. The work shows that the data-driven PIESRGAN subfilter model can very accurately reproduce direct numerical simulation data on much coarser meshes, which is hardly possible with classical subfilter models, and enables studying statistical processes more efficiently due to the smaller computing cost.

Applying Physics-Informed Enhanced Super-Resolution Generative Adversarial Networks to Turbulent Non-Premixed Combustion on Non-Uniform Meshes and Demonstration of an Accelerated Simulation Workflow

This paper extends the methodology to use physics-informed enhanced super-resolution generative adversarial networks (PIESRGANs) for LES subfilter modeling in turbulent flows with finite-rate chemistry and shows a successful application to a non-premixed temporal jet case. This is an important topic considering the need for more efficient and carbon-neutral energy devices to fight the climate change. Multiple a priori and a posteriori results are presented and discussed. As part of this, the impact of the underlying mesh on the prediction quality is emphasized, and a multi-mesh approach is developed. It is demonstrated how LES based on PIESRGAN can be employed to predict cases at Reynolds numbers which were not used for training. Finally, the amount of data needed for a successful prediction is elaborated.

Towards prediction of turbulent flows at high Reynolds numbers using high performance computing data and deep learning

In this paper, deep learning (DL) methods are evaluated in the context of turbulent flows. Various generative adversarial networks (GANs) are discussed with respect to their suitability for understanding and modeling turbulence. Wasserstein GANs (WGANs) are then chosen to generate small-scale turbulence. Highly resolved direct numerical simulation (DNS) turbulent data is used for training the WGANs and the effect of network parameters, such as learning rate and loss function, is studied. Qualitatively good agreement between DNS input data and generated turbulent structures is shown. A quantitative statistical assessment of the predicted turbulent fields is performed.

Pandemic Drugs at Pandemic Speed: Accelerating COVID-19 Drug Discovery with Hybrid Machine Learning- and Physics-based Simulations on High Performance Computers

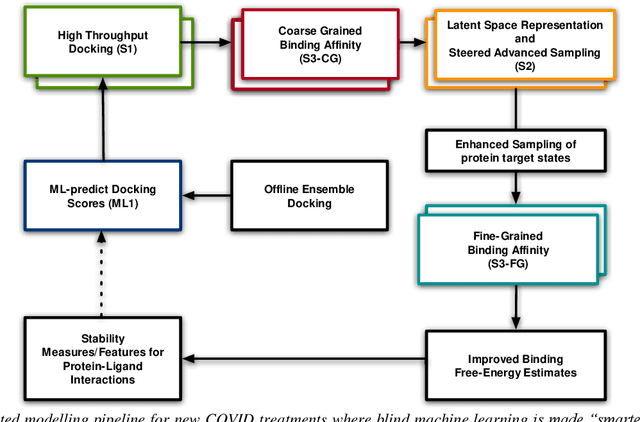
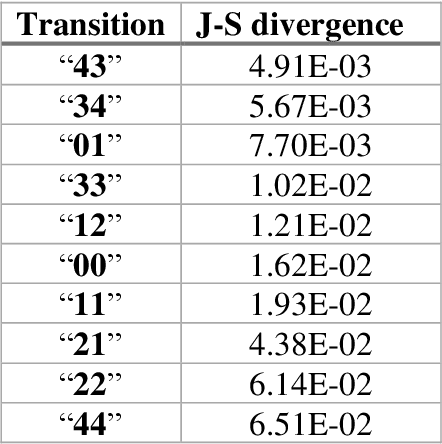
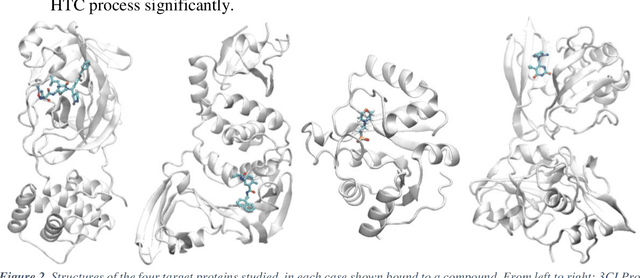
The race to meet the challenges of the global pandemic has served as a reminder that the existing drug discovery process is expensive, inefficient and slow. There is a major bottleneck screening the vast number of potential small molecules to shortlist lead compounds for antiviral drug development. New opportunities to accelerate drug discovery lie at the interface between machine learning methods, in this case developed for linear accelerators, and physics-based methods. The two in silico methods, each have their own advantages and limitations which, interestingly, complement each other. Here, we present an innovative method that combines both approaches to accelerate drug discovery. The scale of the resulting workflow is such that it is dependent on high performance computing. We have demonstrated the applicability of this workflow on four COVID-19 target proteins and our ability to perform the required large-scale calculations to identify lead compounds on a variety of supercomputers.

Using Physics-Informed Super-Resolution Generative Adversarial Networks for Subgrid Modeling in Turbulent Reactive Flows

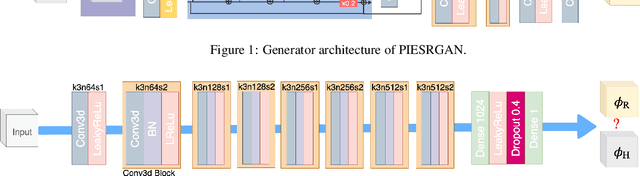
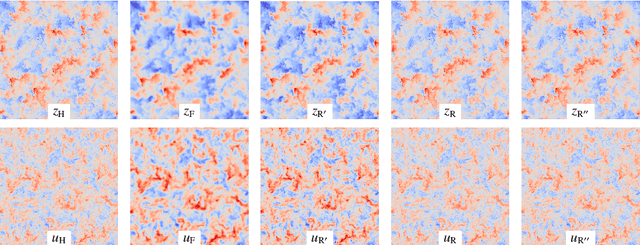
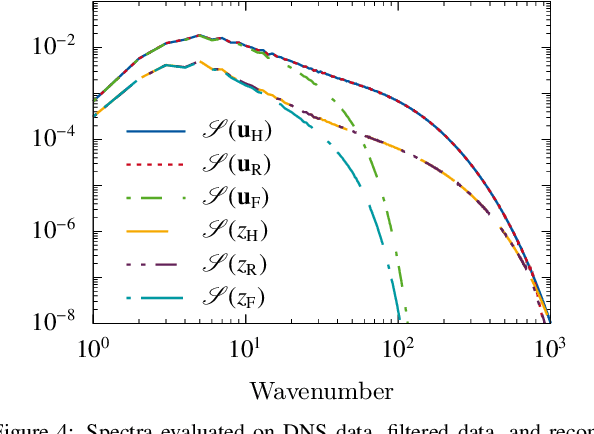
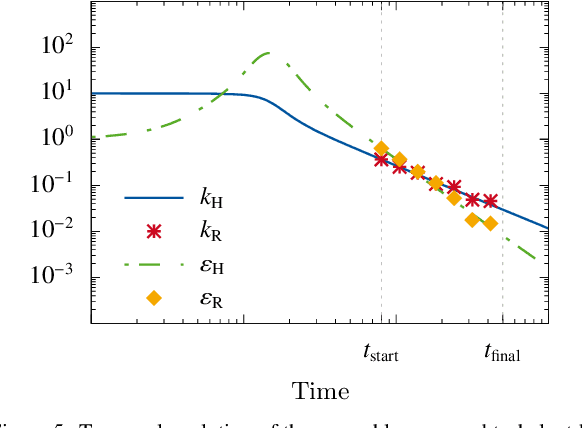
Turbulence is still one of the main challenges for accurately predicting reactive flows. Therefore, the development of new turbulence closures which can be applied to combustion problems is essential. Data-driven modeling has become very popular in many fields over the last years as large, often extensively labeled, datasets became available and training of large neural networks became possible on GPUs speeding up the learning process tremendously. However, the successful application of deep neural networks in fluid dynamics, for example for subgrid modeling in the context of large-eddy simulations (LESs), is still challenging. Reasons for this are the large amount of degrees of freedom in realistic flows, the high requirements with respect to accuracy and error robustness, as well as open questions, such as the generalization capability of trained neural networks in such high-dimensional, physics-constrained scenarios. This work presents a novel subgrid modeling approach based on a generative adversarial network (GAN), which is trained with unsupervised deep learning (DL) using adversarial and physics-informed losses. A two-step training method is used to improve the generalization capability, especially extrapolation, of the network. The novel approach gives good results in a priori as well as a posteriori tests with decaying turbulence including turbulent mixing. The applicability of the network in complex combustion scenarios is furthermore discussed by employing it to a reactive LES of the Spray A case defined by the Engine Combustion Network (ECN).

Deep learning at scale for subgrid modeling in turbulent flows

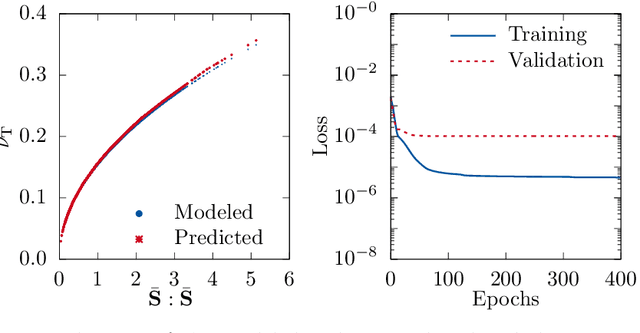
Modeling of turbulent flows is still challenging. One way to deal with the large scale separation due to turbulence is to simulate only the large scales and model the unresolved contributions as done in large-eddy simulation (LES). This paper focuses on two deep learning (DL) strategies, regression and reconstruction, which are data-driven and promising alternatives to classical modeling concepts. Using three-dimensional (3-D) forced turbulence direct numerical simulation (DNS) data, subgrid models are evaluated, which predict the unresolved part of quantities based on the resolved solution. For regression, it is shown that feedforward artificial neural networks (ANNs) are able to predict the fully-resolved scalar dissipation rate using filtered input data. It was found that a combination of a large-scale quantity, such as the filtered passive scalar itself, and a small-scale quantity, such as the filtered energy dissipation rate, gives the best agreement with the actual DNS data. Furthermore, a DL network motivated by enhanced super-resolution generative adversarial networks (ESRGANs) was used to reconstruct fully-resolved 3-D velocity fields from filtered velocity fields. The energy spectrum shows very good agreement. As size of scientific data is often in the order of terabytes or more, DL needs to be combined with high performance computing (HPC). Necessary code improvements for HPC-DL are discussed with respect to the supercomputer JURECA. After optimizing the training code, 396.2 TFLOPS were achieved.

A graphical heuristic for reduction and partitioning of large datasets for scalable supervised training

A scalable graphical method is presented for selecting, and partitioning datasets for the training phase of a classification task. For the heuristic, a clustering algorithm is required to get its computation cost in a reasonable proportion to the task itself. This step is proceeded by construction of an information graph of the underlying classification patterns using approximate nearest neighbor methods. The presented method constitutes of two approaches, one for reducing a given training set, and another for partitioning the selected/reduced set. The heuristic targets large datasets, since the primary goal is significant reduction in training computation run-time without compromising prediction accuracy. Test results show that both approaches significantly speed-up the training task when compared against that of state-of-the-art shrinking heuristic available in LIBSVM. Furthermore, the approaches closely follow or even outperform in prediction accuracy. A network design is also presented for the partitioning based distributed training formulation. Added speed-up in training run-time is observed when compared to that of serial implementation of the approaches.

On the self-similarity of line segments in decaying homogeneous isotropic turbulence

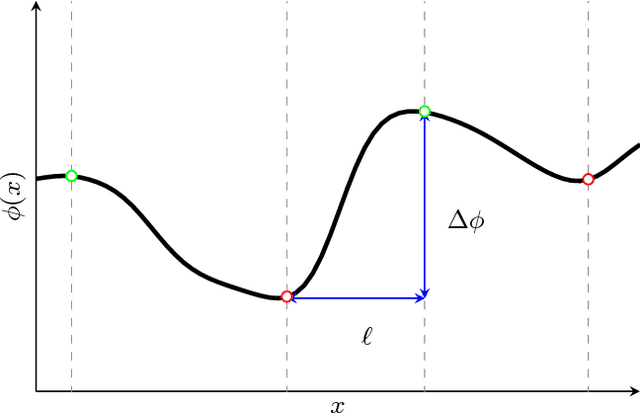
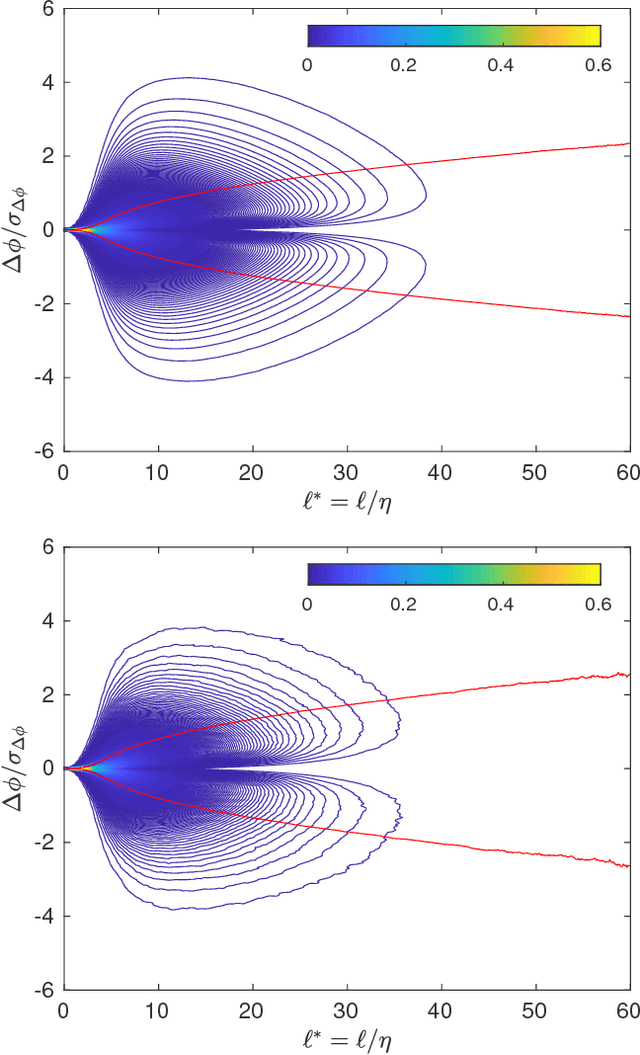
The self-similarity of a passive scalar in homogeneous isotropic decaying turbulence is investigated by the method of line segments (M. Gauding et al., Physics of Fluids 27.9 (2015): 095102). The analysis is based on a highly resolved direct numerical simulation of decaying turbulence. The method of line segments is used to perform a decomposition of the scalar field into smaller sub-units based on the extremal points of the scalar along a straight line. These sub-units (the so-called line segments) are parameterized by their length $\ell$ and the difference $\Delta\phi$ of the scalar field between the ending points. Line segments can be understood as thin local convective-diffusive structures in which diffusive processes are enhanced by compressive strain. From DNS, it is shown that the marginal distribution function of the length~$\ell$ assumes complete self-similarity when re-scaled by the mean length $\ell_m$. The joint statistics of $\Delta\phi$ and $\ell$, from which the local gradient $g=\Delta\phi/\ell$ can be defined, play an important role in understanding the turbulence mixing and flow structure. Large values of $g$ occur at a small but finite length scale. Statistics of $g$ are characterized by rare but strong deviations that exceed the standard deviation by more than one order of magnitude. It is shown that these events break complete self-similarity of line segments, which confirms the standard paradigm of turbulence that intense events (which are known as internal intermittency) are not self-similar.