Generalization over different cellular automata rules learned by a deep feed-forward neural network

To test generalization ability of a class of deep neural networks, we randomly generate a large number of different rule sets for 2-D cellular automata (CA), based on John Conway's Game of Life. Using these rules, we compute several trajectories for each CA instance. A deep convolutional encoder-decoder network with short and long range skip connections is trained on various generated CA trajectories to predict the next CA state given its previous states. Results show that the network is able to learn the rules of various, complex cellular automata and generalize to unseen configurations. To some extent, the network shows generalization to rule sets and neighborhood sizes that were not seen during the training at all.

On the self-similarity of line segments in decaying homogeneous isotropic turbulence

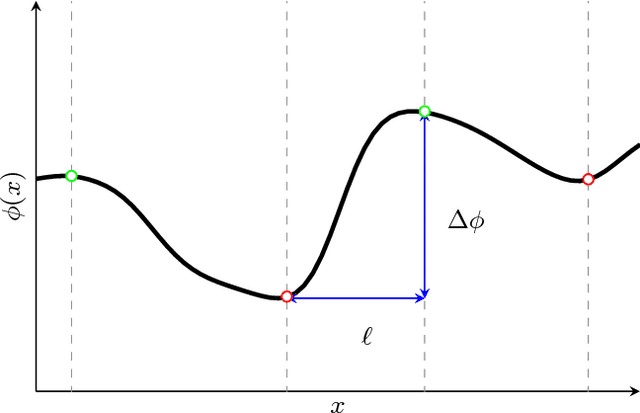
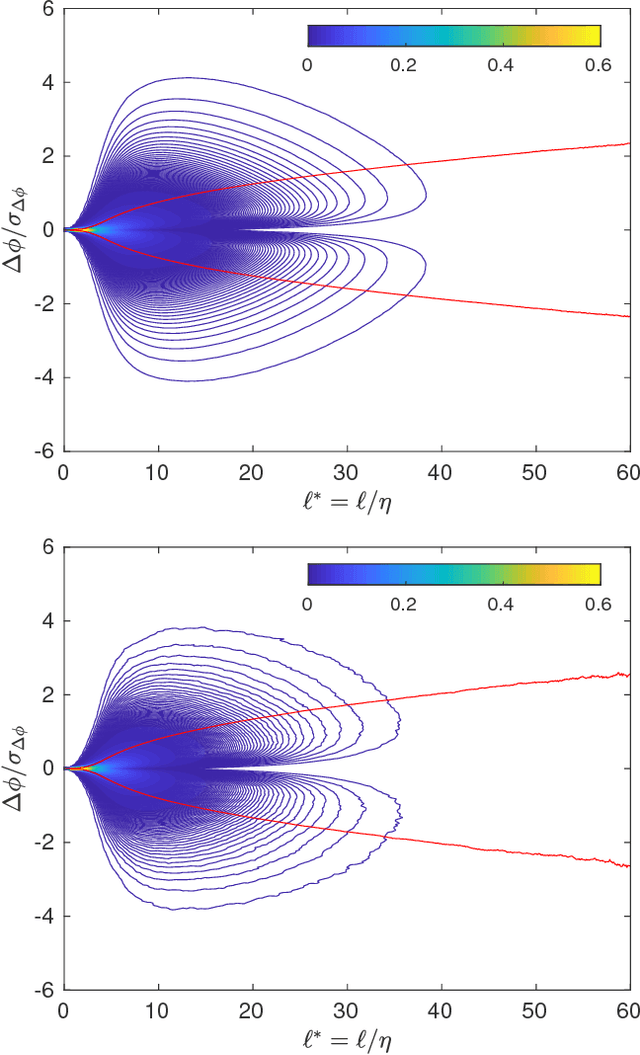
The self-similarity of a passive scalar in homogeneous isotropic decaying turbulence is investigated by the method of line segments (M. Gauding et al., Physics of Fluids 27.9 (2015): 095102). The analysis is based on a highly resolved direct numerical simulation of decaying turbulence. The method of line segments is used to perform a decomposition of the scalar field into smaller sub-units based on the extremal points of the scalar along a straight line. These sub-units (the so-called line segments) are parameterized by their length $\ell$ and the difference $\Delta\phi$ of the scalar field between the ending points. Line segments can be understood as thin local convective-diffusive structures in which diffusive processes are enhanced by compressive strain. From DNS, it is shown that the marginal distribution function of the length~$\ell$ assumes complete self-similarity when re-scaled by the mean length $\ell_m$. The joint statistics of $\Delta\phi$ and $\ell$, from which the local gradient $g=\Delta\phi/\ell$ can be defined, play an important role in understanding the turbulence mixing and flow structure. Large values of $g$ occur at a small but finite length scale. Statistics of $g$ are characterized by rare but strong deviations that exceed the standard deviation by more than one order of magnitude. It is shown that these events break complete self-similarity of line segments, which confirms the standard paradigm of turbulence that intense events (which are known as internal intermittency) are not self-similar.